РАЗРАБОТКА МЕТОДИКИ МОДЕЛИРОВАНИЯ МИКРОРЕЛЬЕФА МЕСТНОСТИ

В настоящее время наблюдается постоянный рост сложности разрабатываемой аппаратуры и средств автоматизации исследований, систем формирования и обработки первичной информации. Одновременно повышаются требования к эффективности систем управления, применяемых в различных областях машиностроения, к сокращению сроков исследования и разработки автоматизированных систем управления

Практически любая задача статистического моделирования содержит в качестве самостоятельного этапа получение реализаций случайных величин (скалярных или векторных) с заданными законами распределения.

Методами моделирования случайных величин посвящено много статей и монографий

Решение различных задач математического моделирования для анализа функционирования систем, возникающих в кибернетике, радиотехнике, гидро- и аэродинамике, метеорологии и других областях науки и техники, приводит к необходимости получения на ЭВМ реализаций случайных полей с заданными статистическими характеристиками.

Модели случайных полей используются для имитации фона в оптико-электронных системах, при описании свойств рельефа земной поверхности в решении задач оценки эффективности специализированных средств, для моделирования метео-полей, при исследовании колебаний механических систем, а также применяются в устройствах фильтрации и кодирования изображений.

В задачах моделирований случайных полей особое значение имеют методы, позволяющие строить простые, легко реализуемые алгоритмы, сокращать затраты машинного времени. Время счета на ЭВМ, требуемое для получения реализаций случайных полей, оказывается во много раз большим, чем время, необходимое для моделирования случайных процессов. Причем трудоемкость цифрового моделирования поля резко возрастает с увеличением размерности его аргумента и уменьшения шага дискретизации

В данной работе ставится цель разработки методики моделирования микрорельефа местности для возможности его использования при разработке имитационных моделей на ЭВМ. Для достижения поставленной цели необходимо привести математическую модель микрорельефа местности и разработать алгоритм его моделирования.

Микрорельеф местности моделируется как случайное однородное и изотропное поле на плоскости:

где

Рассматриваемое поле может быть смоделировано при помощи неканонического представления в виде следующей модели

где

Для моделирования параметров

где

Случайный вектор

где

В качестве произвольной функции распределения вероятности  воспользуемся распределением Рэлея. Найдем моделирующий алгоритм случайной величины  

1) запишем закон распределения Рэлея:

2) найдем обратную функцию закона распределения

где

Выразим  из уравнения (9): 

Таким образом, уравнение (10) — алгоритм моделирования случайной величины

Для моделирования случайного изотропного поля воспользуемся заданной корреляционной функцией

где

При необходимости можно воспользоваться различными корреляционными функциями и соответствующим им спектральным плотностям, например, такими как:

Для моделирования микрорельефа местности необходимо определить следующие исходные данные:

– координаты узлов на плоскости

– корреляционную функцию

– математическое ожидание высот микрорельефа местности

– среднее квадратичное отклонение высот микрорельефа

– число членов неканонического разложения

– радиус корреляции высот

После определения исходных данных необходимо провести предварительные расчеты, а именно:

– определить нормирующий коэффициент, обеспечивающий выполнение равенства

– выбрать функцию распределения

Проведя подготовительные вычисления, можно начать моделировать микрорельеф местности. На рисунке 1 показан алгоритм моделирования высот микрорельефа местности, где

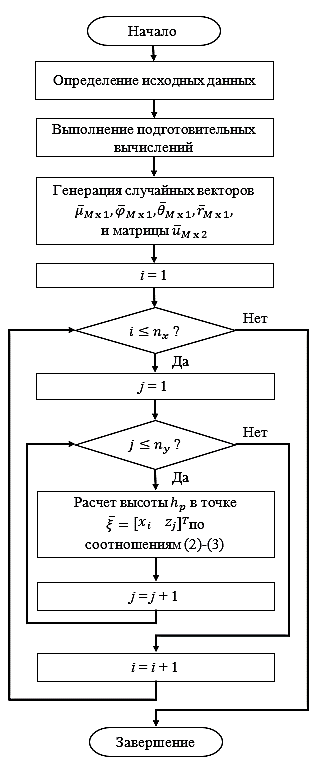
Рисунок 1 - Блок-схема алгоритма моделирования высот микрорельефа местности

DOI:10.60797/IRJ.2025.155.64.1

Моделирование проводилось при зависимостях, изложенных в разделе 1 и при следующих исходных данных:

– координаты x и z на плоскости определены на интервале [-10, 10] м с шагом 0,1 м;

– математическое ожидание высот микрорельефа местности

– среднее квадратичное отклонение высот микрорельефа

– число членов неканонического разложения

– радиус корреляции высот

На рисунке 2 показаны реализации случайного микрорельефа местности в виде цветовой карты высот, а на рисунке 3 показана случайная поверхность — микрорельеф местности.

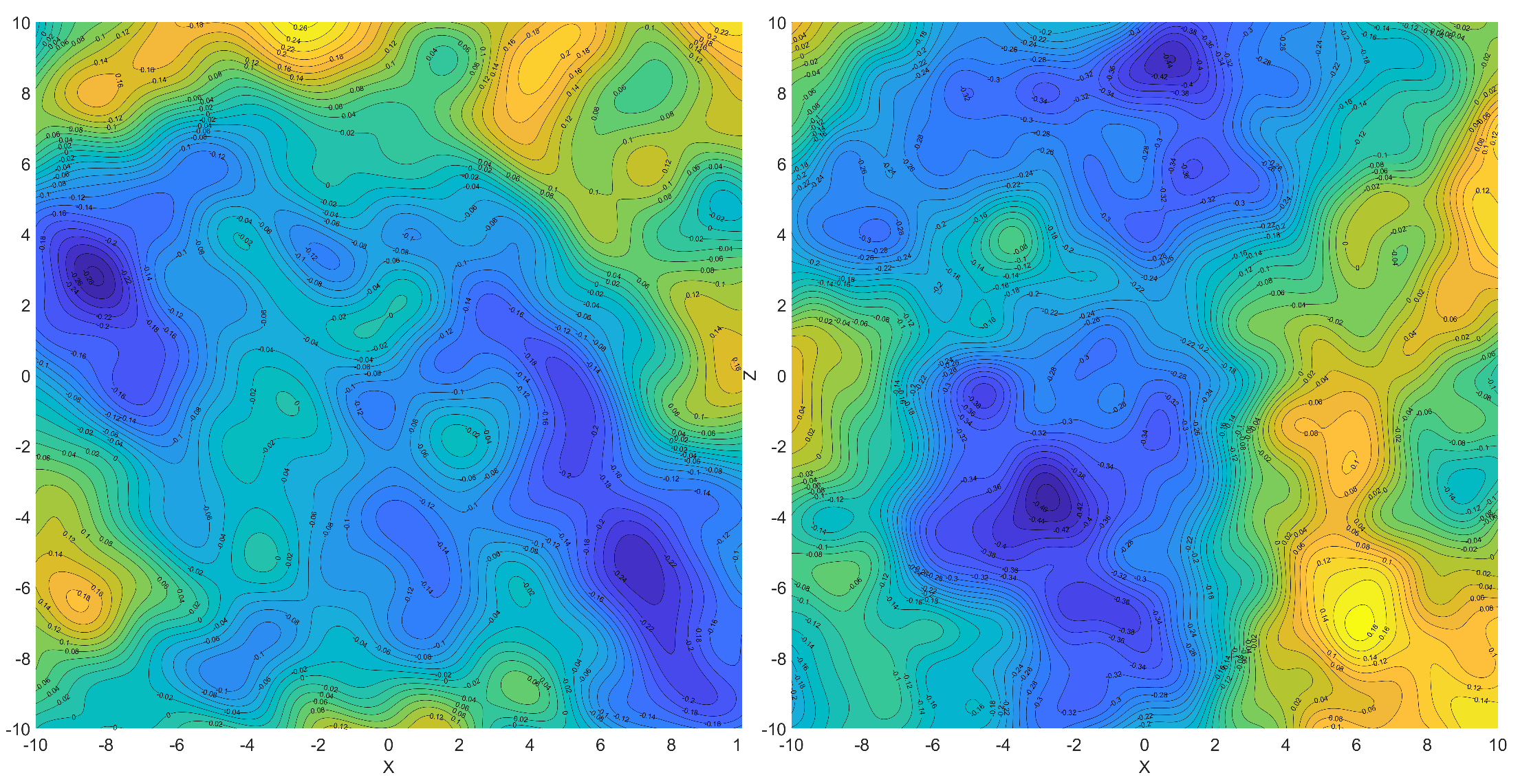
Рисунок 2 - Карты высот случайных микрорельефов местности

DOI:10.60797/IRJ.2025.155.64.2

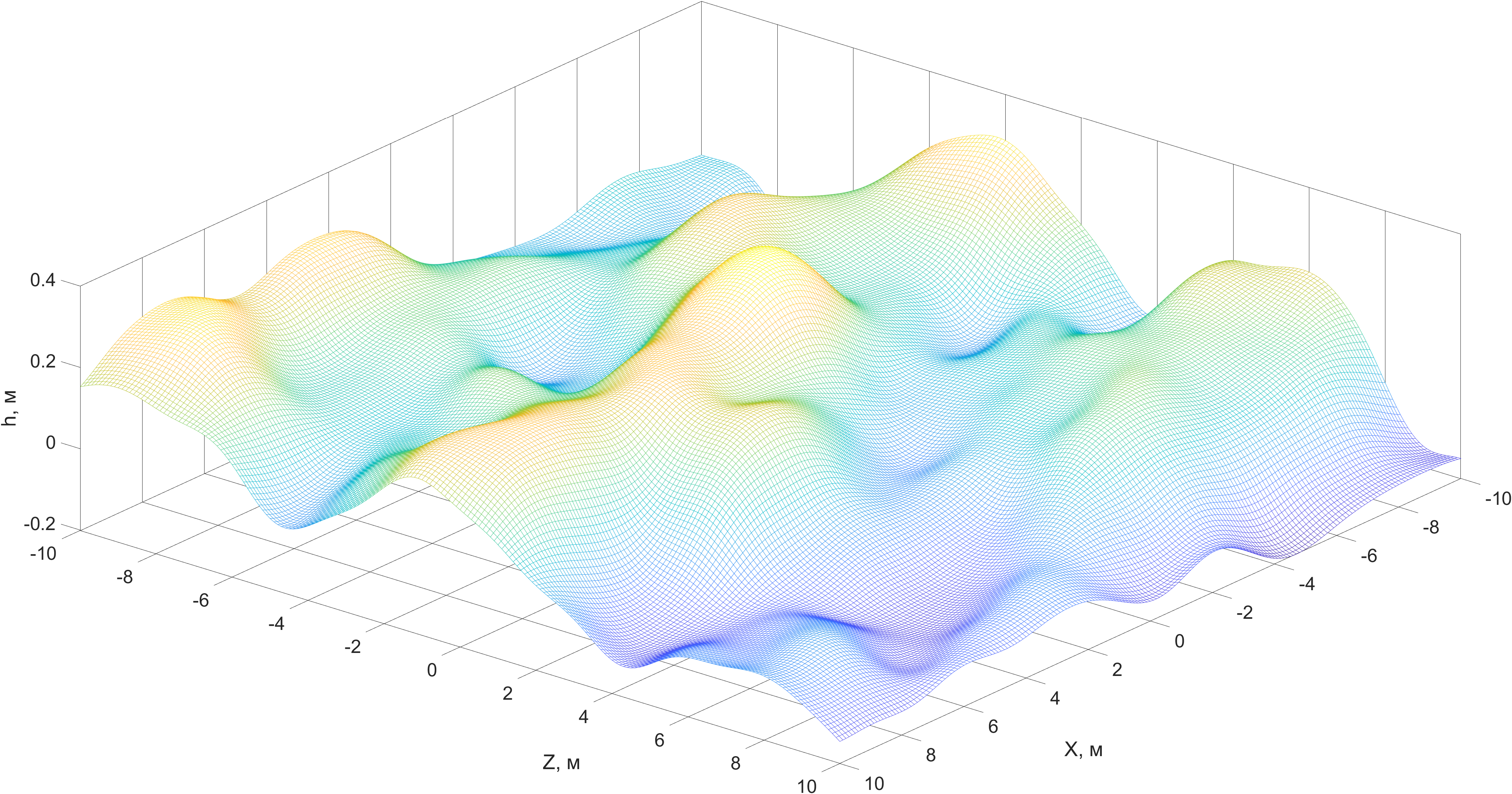
Рисунок 3 - Поверхность микрорельефа местности

DOI:10.60797/IRJ.2025.155.64.3

Разработана методика моделирования случайного микрорельефа местности как изотропное поле с заданными параметрами. По известным математическим моделям разработан алгоритм моделирования случайного поля. Смоделированы примеры реализации случайных микрорельефов местности. Новизна и актуальность заключается в предложенном алгоритме моделирования по известным математическим моделям, которые описывают случайные процессы. Также предложена методика применения произвольной функции распределения вероятности для моделирования случайных параметров поля.

Разработанный алгоритм является универсальным и может быть использован не только для имитации микрорельефа местности, но и для моделирования крупных территорий с различным рельефом, а также представления различных метео-полей, гравитационных, электромагнитных и других полей.