Наши журналы
Опубликовать статью Вход и регистрация
Расширенный поиск
Разделы статьи
Рецензия

К ВОПРОСУ ОБ ИССЛЕДОВАНИИ ПОВЕДЕНИЯ ТРАЕКТОРИЙ ТОЧЕЧНОГО ОТОБРАЖЕНИЯ ПЛОСКОСТИ В ПЛОСКОСТЬ В УДАЛЕННЫХ ЧАСТЯХ ФАЗОВОЙ ПЛОСКОСТИ

Научная статья
Антоновская О. Г.
Бесклубная А. В.
DOI:
https://doi.org/10.60797/IRJ.2025.155.25
Выпуск: № 5 (155), 2025
Предложена:
15.01.2025
Принята:
24.04.2025
Опубликована:
16.05.2025
431
2
XML
PDF

Аннотация

Вопрос об «устойчивости-неустойчивости бесконечности» является важным вопросом исследования динамики системы на плоскости. В настоящей работе для решения этого вопроса предложена методика исследования поведения траекторий точечного отображения плоскости в плоскость, использующая замену переменных, переводящую плоскость во внутренность круга единичного радиуса (т.е. бесконечно удаленную часть плоскости в конечную). На примере изучения конкретных квазилинейных систем показана целесообразность применения предложенной методики для получения наглядной картины поведения траекторий точечного отображения на всей фазовой плоскости, в том числе и в ее удаленных частях. Отмечено, что использование указанной замены позволяет подтвердить проведенное ранее изучение влияния характера нелинейности на результаты качественного исследования систем с малым параметром при нелинейных членах асимптотическими методами.

Ключевые слова:
динамика системы, метод точечных отображений, фазовое пространство, траектория системы, устойчивость.

1. Введение

Известно, что в основе наиболее эффективного подхода к исследованию тех задач теории нелинейных колебаний

, в которых классические методы оказываются малоэффективными, лежит метод точечных отображений
, в последние годы все шире и чаще привлекающийся как для рассмотрения общих вопросов теории динамических систем, так и для решения различных прикладных задач. Следует отметить, что изучение многих типов динамических систем может быть сведено к построению и исследованию точечного преобразования некоторого множества в себя. То есть задачу изучения динамической системы можно разбить на два основных этапа. Целью первого этапа является выбор некоторого геометрического образа (прямой, плоскости, пространства или какой-то то их части), к изучению точечного отображения которого в себя сводится изучение системы. На втором этапе строится точечное отображение в явном виде, если это возможно. Если получение его в явном виде невозможно или затруднительно, то применяются приближенные (в том числе и асимптотические) методы, а также те или иные численные методы. И вместо исходной динамической системы исследуется соответствующее ей точечное отображение, и уже по поведению его траекторий делаются выводы о поведении динамической системы при тех или иных значениях параметров.

2. Основная часть

Применение метода точечных отображений для построения математических моделей дискретных систем второго порядка, а также его использование при исследовании непрерывных систем на плоскости, предоставляет возможность получения адекватной информации о динамике систем математическими методами

.

При изучении качественной картины поведения траекторий точечных отображений в конкретных задачах большую роль играет исследование поведения траекторий в удаленных частях фазовой плоскости. Существует математический аппарат, позволяющий решать задачу, совершив замену переменных, которая перевела бы бесконечно удаленную часть плоскости в конечную. Этого, например, можно достичь с помощью преобразования Бендиксона

.

;
,

которое переводит бесконечно удаленные точки плоскости x0, y0 в начало координат плоскости u0, v0. Удобно пользоваться также преобразованием Пуанкаре

, переводящим плоскость x0, y0 на сферу радиуса 1, касающуюся плоскости x0, y0 в начале координат

,
,

где τ0 есть тангенс направления на исследуемую точку. Координатные линии z0=const и τ0=const суть на плоскости прямые, параллельные оси y, и прямые, проходящие через начало координат. На сфере же они являются большими кругами, проходящими через взаимно перпендикулярные диаметры. Рассмотрение производится на плоскости τ0, z0, касательной к сфере, куда точки сферы проектируются из ее центра.

Заметим, что не менее удобным при исследовании поведения траекторий точечного отображения в удаленных частях плоскости может быть использование замены переменных

.

(1)
(2)

непосредственно переводящей плоскость x0, y0 во внутренность круга единичного радиуса u02+v02<1 (при этом бесконечно удаленным точкам плоскости соответствует окружность единичного радиуса u02+v02=1). Заметим, что отображения (1) и (2) являются взаимно-непрерывными и взаимно-однозначными, т.к. их якобианы отличны от нуля. Исключение для (2) составляют точки окружности u02+v02=1. При этом, поскольку

,
,

то направление на исследуемую точку при замене (2) остается неизменным, изменение претерпевает лишь расстояние до нее от начала координат (при x0=y0=0 u0=v0=0).

(3)

примут вид

(4)

а значит

\overline{u}_0^2+\overline{v}_0^2&lt;1
 при 
u_0^2+v_0^2&lt;1
. Доопределив (4) на окружности по правилу

в случае существования соответствующих пределов, получим точечное отображение единичного круга

 в себя, качественное поведение траекторий которого отражает качественное поведение траекторий исходного отображения (3) в конечной части плоскости x0, y0, причем поведение траекторий (4) в окрестности окружности
 отражает поведение траекторий (3) в удаленных частях плоскости, при этом картина обладает большей наглядностью
.

Для примера рассмотрим следующие системы.

1. Уравнение Дуффинга

(5)

где 0<μ<<1, A>0. Известно

, что исследование поведения траекторий (5) может быть сведено к изучению поведения траекторий точеного отображения 

(6)
(7)

с точностью до величин порядка μ2 приближающего точечное отображение, порождаемое траекториями соответствующей (5) системы на секущей поверхности

.

В переменных u0, v0 точечное отображение

 (6)-(7) примет вид

(8)

допускающий численное исследование траекторий на всем множестве

.

Окружность

 является инвариантным многообразием (8). В точках этой окружности

(9)

Таким образом, любая точка окружности 

 является неподвижной точкой отображения 
(т.е. каждой такой точке соответствует цикл 4 порядка отображения
 — рисунок 1 — а именно: 
). А вопрос об устойчивости окружности
 легко решается посредством сравнения величин 
 и 
 вблизи окружности (
0&lt;u_0^2+v_0^2&lt;\tilde{u}^2+\tilde{v}^2 &lt; 1
).

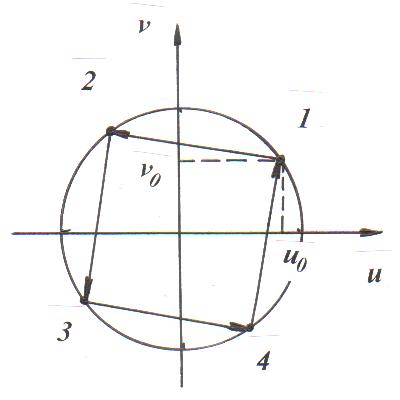
Поведение точечного отображения на окружности u02+v02=1 в случае уравнения Дуффинга

Рисунок 1 - Поведение точечного отображения на окружности u02+v02=1 в случае уравнения Дуффинга

DOI:10.60797/IRJ.2025.155.25.1
Численное исследование поведения траекторий (8) показало, что
 всегда является притягивающим множеством
(что подтверждает результаты статьи
об «устойчивости бесконечности» в случае полиномиальной нелинейности системы). Следует отметить, что изучение поведения точечного отображения
 в переменных u0, v0 позволяет не только установить факт рождения устойчивой инвариантной кривой при переходе через границу устойчивости Nφ на плоскости параметров, но и показать, что в конечной части фазовой плоскости x0, y0 (во внутренности круга
u_0^2+v_0^2&lt;1
) существует неустойчивое инвариантное многообразие соответствующего точечного отображения, причем отсутствие притягивающего множества в ограниченной части плоскости x0, y0 (во внутренности круга
u_0^2+v_0^2&lt;1
) имеет место после слияния устойчивой инвариантной кривой с неустойчивой и их исчезновения.

2. Уравнение синхронизуемого осциллятора с нелинейностью вида кубической параболы:

(10)

где 0<μ<<1, A>0. Известно

, что исследование поведения траекторий (5) может быть сведено к изучению поведения траекторий точеного отображения 

(11)
(12)

с точностью до величин порядка μ2 приближающего точечное отображение, порождаемое траекториями соответствующей (10) системы на секущей поверхности t=[t/(2π)]2π.

В переменных u0, v0 точечное отображение

 (11)-(12) примет вид

(13)

допускающий численное исследование траекторий на всем множестве

.

Окружность

 является инвариантным многообразием (8). В точках этой окружности

(14)

Таким образом, любая точка окружности 

 является неподвижной точкой отображения 
(т.е. каждой такой точке соответствует цикл 2 порядка отображения
 – рисунок 2 — а именно: 
). А вопрос об устойчивости окружности
 легко решается посредством сравнения величин 
 и 
 вблизи окружности (
0&lt;u_0^2+v_0^2&lt;\tilde{u}^2+\tilde{v}^2 &lt; 1
).

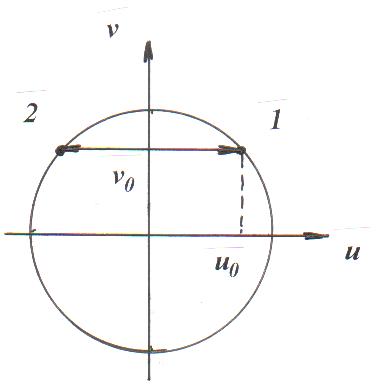
Поведение точечного отображения на окружности u02+v02=1 в случае нелинейности типа кубической параболы

Рисунок 2 - Поведение точечного отображения на окружности u02+v02=1 в случае нелинейности типа кубической параболы

DOI:10.60797/IRJ.2025.155.25.2
Численное исследование поведения траекторий (13) показало, что
 всегда является притягивающим множеством (что подтверждает результаты статьи
об «устойчивости бесконечности» в случае полиномиальной нелинейности системы).

3. Уравнение синхронизуемого осциллятора с типа Ван-дер-Поля

:

(15)

где 0<μ<<1, A>0. Известно

, что исследование поведения траекторий (15) может быть сведено к изучению поведения траекторий точеного отображения 

(16)
(17)

с точностью до величин порядка μ2 приближающего точечное отображение, порождаемое траекториями соответствующей (15) системы на секущей поверхности

.

В переменных u0, v0 точечное отображение

 (11)-(12) примет вид

(18)

допускающий численное исследование траекторий на всем множестве

.

Окружность

 является инвариантным многообразием (18). В точках этой окружности

(19)

т.е. отображение на окружности

 является тождественным.

Численное исследование поведения траекторий (19) показало, что

 всегда является притягивающим множеством (что подтверждает результаты статьи
об «устойчивости бесконечности» в случае полиномиальной нелинейности системы).

4. Уравнение квазигармонического осциллятора с квадратичным трением

.

(20)

где 0<μ<<1, A>0. Известно

, что исследование поведения траекторий (20) может быть сведено к изучению поведения траекторий точеного отображения 

(21)
(22)

с точностью до величин порядка μ2 приближающего точечное отображение, порождаемое траекториями соответствующей (20) системы на секущей поверхности

.

В переменных u0, v0 точечное отображение

 (21)-(22) примет вид

(23)

допускающий численное исследование траекторий на всем множестве

.

Окружность

 является инвариантным многообразием (23). В точках этой окружности

(24)

Таким образом, любая точка окружности 

 является неподвижной точкой отображения 
(т.е. каждой такой точке соответствует цикл 2 порядка отображения
 – рисунок 3 – а именно: 
). А вопрос об устойчивости окружности
 легко решается посредством сравнения величин 
 и 
 вблизи окружности (
0&lt;u_0^2+v_0^2&lt;\tilde{u}^2+\tilde{v}^2&lt; 1
).

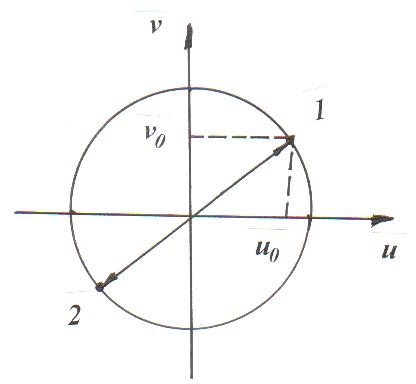
Поведение точечного отображения на окружности u02+v02=1 в случае квадратичного трения в системе

Рисунок 3 - Поведение точечного отображения на окружности u02+v02=1 в случае квадратичного трения в системе

DOI:10.60797/IRJ.2025.155.25.3
Численное исследование поведения траекторий (23) показало, что
 всегда является притягивающим множеством (что подтверждает результаты статьи
об «устойчивости бесконечности»).

5. Уравнение синхронизуемого осциллятора с нелинейностью вида sgn 

(25)

где 0<μ<<1, A>0. Известно

, что исследование поведения траекторий (20) может быть сведено к изучению поведения траекторий точеного отображения 
.

В этом случае точечное отображение 

 (26)-(27) в переменных u0, v0 примет вид

(28)
(29)

допускающий численное исследование траекторий на всем множестве

. Окружность
 является инвариантным многообразием (28)-(29). В точках этой окружности

(30)
(31)

а т.к.

то можно ввести обозначения
,
, а (30)-(31) переписать как

(32)

где

(33)

Т.е. отображение (30)-(31) на окружности 

 есть

\widetilde{\alpha}=\left.\left(\alpha_0-\alpha^*\right)\right|_{\bmod 2 \pi,} 0&lt;\alpha^*&lt;2 \pi,
(34)

или отображение поворота на угол -α*. Таким образом, условия

, 
могут выполняться только если ξ=0, μπ<0, причем отображение становится тождественным. Отображение (34) может иметь циклы порядка n∈N только если существует такое m∈N, что nα*=2πm. Скажем, цикл порядка n=2 может существовать при ξ=0, μπ>1 (при этом отображение (34) таково, что
 является тождественным отображением на окружности u02+v02=1).

Численное исследование поведения траекторий (30)-(31) показало, что в случае существования устойчивой неподвижной точки областью ее притяжения является все множество u02+v02<1 

. В случае, когда неподвижных точек у (30)-(31) нет, либо они неустойчивы, но 
|\xi|&lt;|\xi_{ас}|=\sqrt{2/(\mu\pi)-1}
 0<μπ<<1, у отображения (30)-(31) всегда существует устойчивое многообразие при u02+v02<1, все более расширяющееся при |ξ|→|ξac| 
. Таким образом, в случае существования устойчивой неподвижной точки (25) областью ее притяжения является все фазовое пространство. При |ξ|→|ξac| у отображения (25) всегда существует притягивающее множество в конечной части плоскости, областью притяжения которого является все фазовое пространство. При |ξ|→|ξac| все траектории (25), отличные от существующих неподвижных точек, уходят в бесконечность
. Следует также отметить, что изучение поведения траекторий
 посредством перехода к переменным u0, v0 позволяет установить факт рождения устойчивой инвариантной кривой при переходе через границу Nφ и ее ухода в бесконечность при |ξ|→|ξac|.

Следует отметить, что предложенный выше подход к исследованию поведения траекторий точечного отображения позволил на только подтвердить, но и уточнить полученные результаты.

3. Заключение

В работе рассмотрена методика изучения поведения траекторий двумерного точечного отображения в удаленных частях фазовой плоскости, основанная на отображении всех точек фазовой плоскости внутрь круга единичного радиуса. Это отображение является взаимно однозначным для точек конечной части плоскости, поэтому выводы о поведении траекторий системы обладают не только наглядностью, но и достоверностью

, а методика позволяет не только решать вопрос об «устойчивости или неустойчивости бесконечности», но и оценивать характер поведения траекторий в целом. Предложенная методика апробирована на примере изучения отображений, описывающих реальные динамические системы. Динамика рассмотренных систем в конечно части плоскости ранее была рассмотрена в работах
,
,
,
. Поэтому приведенное выше исследование является дополнением и уточнением исследований, проведенных ранее.

Дополнительные материалы

Не указаны

Финансирование

Авторы не получали финансовой поддержки для проведения исследования, написания и публикации статьи

Благодарности

Не указаны

Конфликт интересов

Не указаны

Список литературы

  • Андронов А.А. Теория колебаний / А.А. Андронов, А.А. Витт, С.Э. Хайкин. — Москва : Наука, 1981. — 568 с.

  • Неймарк Ю.И. Метод точечных отображений в теории нелинейных колебаний / Ю.И. Неймарк. — Москва : Наука, 1972. — 472 с.

  • Антоновская О.Г. К исследованию поведения траекторий точечных отображений плоскости в плоскость в удаленных частях фазовой плоскости / О.Г. Антоновская, В.И. Горюнов // Математическое моделирование и оптимальное управление: Вестник ННГУ. — Нижний Новгород, 2002. — № 1 (25). — С. 68–75.

  • Антоновская О.Г. О влиянии насыщения нелинейности на результаты исследования принудительной синхронизации методом приближенных точечных отображений / О.Г. Антоновская // Математическое моделирование и оптимальное управление: Вестник ННГУ. — Нижний Новгород, 1999. — № 2 (21). — С. 198–208.

  • Антоновская О.Г. О влиянии характера нелинейности на результаты исследования синхронизации квазигармонического осциллятора методом приближенных точечных отображений / О.Г. Антоновская, А.В. Бесклубная // Международный научно-исследовательский журнал. — 2021. — № 1 (103). — Ч. 1. — С. 22–29.

  • Антоновская О.Г. Об одном случае исследования принудительной синхронизации методом приближенных точечных отображений / О.Г. Антоновская, М.Н. Зайцева // Международный научно-исследовательский журнал. — 2018. — № 8 (74). — С. 7–14.

  • Калякин Л.А. Анализ модели синхронизации в неизохронной системе / Л.А. Калякин // Журнал вычислительной математики и математической физики. — 2010. — Т. 50. — № 8. — С. 1408–1419.

  • Антоновская О.Г. Исследование синхронизации квазигармонического осциллятора типа Ван-дер-Поля / О.Г. Антоновская, А. В. Бесклубная // Тенденции развития науки и образования. — 2024. — № 2 (106). — Ч. 9. — С. 132–136.

  • Антоновская О.Г. Исследование синхронизации квазигармонического осциллятора с квадратичным трением. / О.Г. Антоновская, А.В. Бесклубная // Тенденции развития науки и образования. — 2023. — № 10 (102). — Ч. 5. —С. 52–56.

  • Антоновская О.Г. Метод точечных отображений в задачах нелинейной динамики / О.Г. Антоновская, В.И. Горюнов. — Гамбург: LAP Lambert Academic Publishing, 2013. — 140 с.

Рецензия

Рецензент:Фазылзянов Роберт Рашидович
1 раунд рецензирования

Информация об авторах

АффилиацияНижегородский государственный архитектурно-строительный университет, Нижний Новгород, Российская Федерация
Роль:Автор
ORCID:0000-0002-5688-7996
АффилиацияНижегородский государственный архитектурно-строительный университет, Нижний Новгород, Российская Федерация
Роль:Автор

Метрика статьи

Просмотров:431
Скачиваний:2
Просмотры
Всего:
Просмотров:431