ИССЛЕДОВАНИЕ УНИВЕРСАЛЬНОГО ФИНИТНО-ВРЕМЕННОГО ОПТИМАЛЬНОГО МЕТОДА ФИЛЬТРАЦИИ И ПРОГНОЗИРОВАНИЯ НАВИГАЦИОННЫХ ДИСКРЕТНЫХ СИГНАЛОВ
ИССЛЕДОВАНИЕ УНИВЕРСАЛЬНОГО ФИНИТНО-ВРЕМЕННОГО ОПТИМАЛЬНОГО МЕТОДА ФИЛЬТРАЦИИ И ПРОГНОЗИРОВАНИЯ НАВИГАЦИОННЫХ ДИСКРЕТНЫХ СИГНАЛОВ
Аннотация
В качестве альтернативы классической фильтрации Калмана и методу прогноза на его основе в исследовательской работе предлагается универсальный финитно-временной оптимальный метод фильтрации и прогнозирования навигационных дискретных сигналов без обратной связи. Рассматриваемый метод отличается универсальностью, простотой в реализации, а параметры качества и динамических характеристик обработки с увеличением объема памяти r (количество результатов измерений) асимптотически стремятся к значениям фильтрации Калмана.
В ходе исследования проводится сравнительный анализ универсального финитно-временного оптимального метода обработки и прогнозирования навигационных сигналов с фильтрацией и методом прогнозирования Калмана по показателям точности, времени переходного процесса, робастности и помехозащищенности. Сравнительный анализ проводится на примере линейной модели измерений с аддитивной погрешностью, где в качестве полезного сигнала используется гауссовский стационарный марковский случайный процесс, а в качестве помехи – некоррелированный стационарный белый гауссовский шум.
В работе приводятся основные достоинства и недостатки рассматриваемых методов обработки. Представлено краткое описание финитно-временного метода фильтрации и прогнозирования без использования обратной связи.
1. Введение
Как известно, в процессе пилотирования и навигации летательного аппарата любые измерения, полученные с датчиков пилотажно-навигационного комплекса, предполагают наличие помех, которые могут быть вызваны как наличием внутренних возмущений и шумов, так и каким-либо воздействием извне. Выделение полезного сигнала измерений на фоне любого рода помех осуществляют фильтры – устройства, в основе которых лежит использование математических алгоритмов. Наиболее используемым на сегодняшний день математическим алгоритмом является рекурсивная фильтрация Калмана, обладающая следующими основными достоинствами: оптимальность по критерию среднего квадрата ошибки оценки, использование всех измерений с момента начала работы при формировании текущих оценок и рекуррентность оценивания сигналов, позволяющая снизить требования к памяти устройства обработки информации. Фильтрация Калмана также имеет и недостатки: использование им рекуррентной обработки возможно лишь при наличии свойства марковости процесса, что делает его ограниченным в использовании, а также, в связи с наличием обратной связи, недостаточные показатели помехозащищенности и робастности алгоритма при изменении как входных параметров, так и параметров обработки сигналов. Кроме того, для оценки качества фильтрации Калмана требуется большой объем вычислительных затрат. Это обусловлено решением сложного дифференциального уравнения Риккати и необходимостью в использовании формирующего фильтра, т.е. представление модели сигналов в пространстве состояний , , .
В качестве альтернативы фильтрации Калмана и методу прогноза на его основе в настоящее время разработан новый метод обработки навигационных измерений: универсальный финитно-временной оптимальный метод фильтрации и прогнозирования навигационных дискретных сигналов . В его основе лежит обработка измерений без обратной связи на финитном интервале времени.
Рассматриваемый метод фильтрации не требует свойства марковости процесса, что делает его универсальным в плане вида используемых сигналов, он инвариантен к наличию или отсутствию свойства коррелированности помехи измерения, а его реализация не предусматривает решения уравнения Риккати, что существенно упрощает вычислительный процесс. Критерий оценки качества, представляющий из себя сумму дисперсий ошибки оценки, с ростом объема памяти (количество результатов измерений) асимптотически стремится к значению фильтрации и методу прогнозирования Калмана, что говорит о его сравнительной точности. Финитно-временное прогнозирование также включает в себя преимущества фильтрации, а по точности и простоте реализации практически не уступает методу прогноза Калмана.
К недостаткам финитно-временного оптимального метода фильтрации и прогнозирования можно отнести наличие требования в накоплении памяти процесса начальных данных, в ходе которого возникает априорная неопределенность, устраняемая при оценке точности алгоритма с течением времени.
В связи с этим, целью исследовательской работы является проведение сравнительного анализа предлагаемого универсального финитно-временного оптимального метода фильтрации и прогнозирования навигационных дискретных сигналов и рекурсивной фильтрации Калмана и его метода прогноза по параметрам точности, времени переходного процесса, робастности и помехозащищенности. В сравнении рассмотрим фильтрацию навигационного измерения и прогнозирование на нескольких интервалах времени. Моделирование исследуемых алгоритмов проводится в программном пакете MathCAD 15.
2. Описание универсального финитно-временного оптимального метода фильтрации и прогнозирования
Пусть исследуемый сигнал на входе фильтра рассматривается как линейная модель измерения навигационного сигнала с аддитивной некоррелированной погрешностью, которая описывается уравнением:
где и
– скалярные значения наблюдаемого и оцениваемого полезного сигналов в
-ый момент времени соответственно;
– значение некоррелированной с сигналом аддитивной помехи.
Для осуществления финитно-временной фильтрации и оценки прогноза, необходимо линейную модель сигнала (1) представить в виде вектора размерностью , где
– количество результатов измерения (объем памяти финитно-временного фильтра), учитываемое в процессе оценки :
В основе финитно-временного метода алгоритма оценивания дискретных сигналов лежит следствие теоремы ортогонального проецирования В. С. Пугачева, по которому определяется оптимальная по критерию среднего квадрата ошибки оценки матрица преобразования размерностью
:
где – взаимная корреляционная матрица размерностью
вектора полезного сигнала
и вектора оцениваемого сигнала
, подаваемого на вход фильтра в
-ый момент времени;
– матрица корреляционных моментов входного сигнала размерностью
, определяемая как:
где и
– корреляционные характеристики полезного сигнала и помехи соответственно.
В случае некоррелированности измерения и помехи, матрица преобразования принимает вид:
Оптимальный вектор оценок финитно-временного алгоритма определяется следующей формулой:
Корреляционная характеристика оптимальной оценки финитно-временного алгоритма размерностью определяется следующей формулой:
Оценить точность финитно-временной фильтрации и оценки прогноза в момент переходного процесса и при установившемся значении в -ый момент времени можно по формуле:
Оптимальная оценка точности финитно-временного алгоритма и оценки прогноза при завершенном переходном процессе в -ый момент времени определяется следующим образом:
После окончания переходного процесса корреляционные матрицы (8) и (9) должны совпасть.
Статистическая оценка дисперсии финитно-временной фильтрации и оценки прогноза в -ый момент времени определяется с помощью следующего соотношения:
где – ошибка фильтрации и оценки прогноза в
-ый момент времени:
где – первая компонента оптимального вектора оценок (6);
– статистическая оценка математического ожидания, определяемая по формуле:
Примечание – Для формул (1)-(12) моменты времени , где
– общее число точек наблюдения в выборочной совокупности (объем выборки).
3. Сравнительный анализ рассматриваемых алгоритмов
В качестве критерия оптимальности условно принимаем дисперсию ошибки оценки. Исследуемым объектом для оценивания используется радиотехнический высотомер, модель измерения которого описывается линейным уравнением (1).
Пусть модель полезного сигнала канала представляет собой гауссовский стационарный марковский случайный процесс первого порядка, корреляционная характеристика которого имеет вид:
где – среднеквадратическое отклонение значения высоты полета (полезного сигнала);
– параметр корреляционной функции;
– дискрет, определяемый теоремой Котельникова.
Модель помехи представляется в виде некоррелированного стационарного белого гауссовского шума, корреляционная характеристика которого имеет вид:
где – среднеквадратическое отклонение белого шума (помехи);
– дельта-функция Дирака.
Сравнительный анализ рассматриваемых алгоритмом фильтраций и прогнозирования выполнен при следующих исходных данных:
– объем выборки = 3000;
– среднеквадратическое отклонение полезного сигнала = 7 м;
– среднеквадратическое отклонение помехи = 5 м;
– параметр корреляционной функции = 0,01 c-1;
– память, требующаяся для финитно-временной обработки = 4;
– дискрет = 4;
– интервалы времени прогноза = 10, 20 с.
Моделирование дисперсий ошибки оценки рассматриваемых фильтраций приведены на рисунках 1-3. Численные результаты обработок занесем в таблицу 1. Обозначения на рисунках следующие:
– для рисунка 1: и
– статистическое и теоретическое значения дисперсий ошибки оценки финитно-временной обработки соответственно;
и
– статистическое и теоретическое значения дисперсий ошибки оценки фильтрации Калмана соответственно.
– для рисунков 2, 3: и
– статистическое и теоретическое значения дисперсий ошибки оценки финитно-временной оценки прогноза соответственно;
и
– статистическое и теоретическое значения дисперсий ошибки оценки прогноза Калмана соответственно.
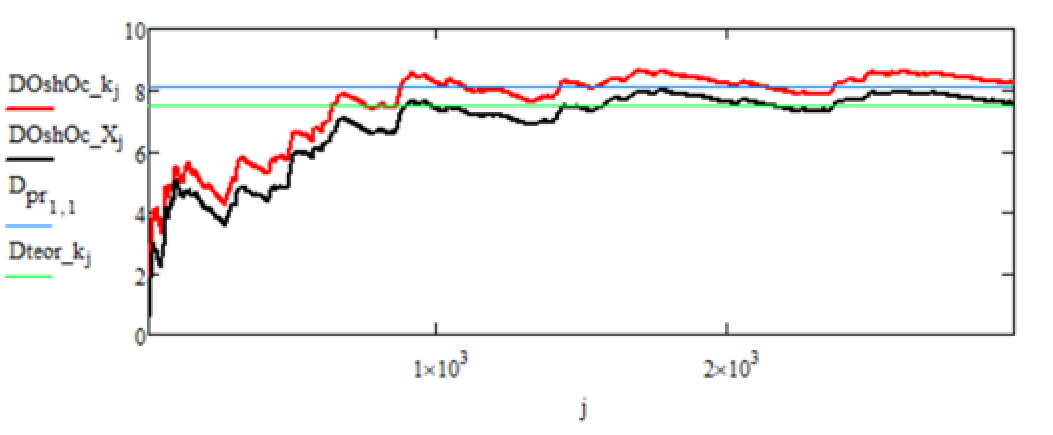
Рисунок 1 - Графики зависимостей теоретических и статистических дисперсий ошибок оценок финитно-временной обработки и фильтрации Калмана на интервале от 0 до N
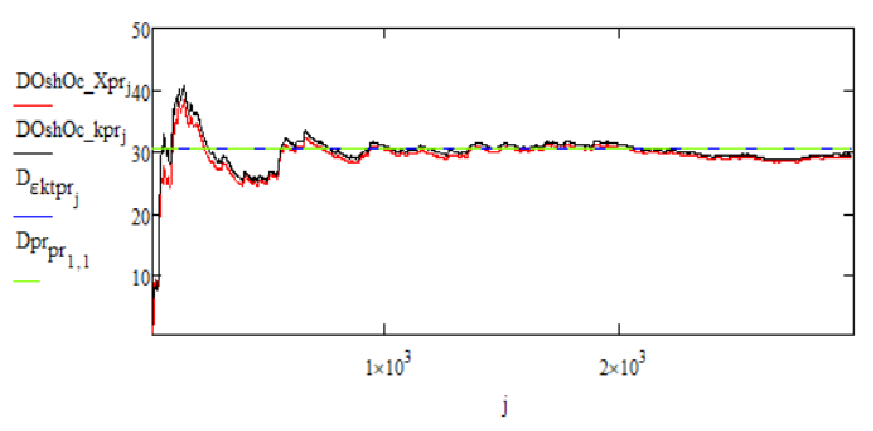
Рисунок 2 - Графики зависимостей теоретических и статистических дисперсий ошибок оценок финитно-временной оценки прогноза и прогноза Калмана на интервале от 0 до N при T = 10 с
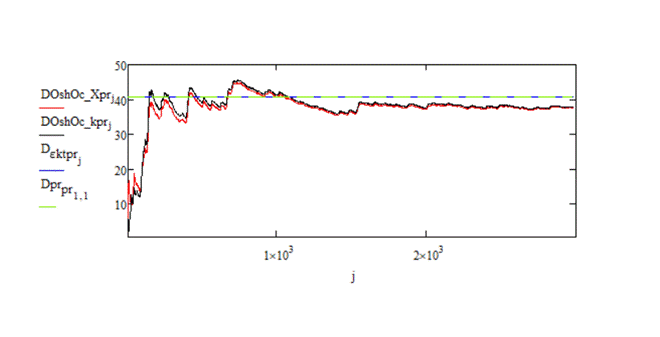
Рисунок 3 - Графики зависимостей теоретических и статистических дисперсий ошибок оценок финитно-временной оценки прогноза и прогноза Калмана на интервале от 0 до N при T = 20 с
Таблица 1 - Численные результаты обработок
Обработка | Интервал времени прогноза Т | Теоретическая точность, м2 | Статистическая точность, м2 | Время переходного процесса, с |
Фильтрация Калмана | - | 7,479 | 8,220 | 651 |
Финитно-временная обработка | 8,088 | 7,549 | 867 | |
Прогноз Калмана | 10 | 30,343 | 29,405 | 686 |
Финитно-временная оценка прогноза | 30,617 | 28,951 | 674 | |
Прогноз Калмана | 20 | 40,617 | 38,353 | 910 |
Финитно-временная оценка прогноза | 40,740 | 38,382 | 896 |
По результатам моделирования, отраженных на рисунках 1-3 и в таблице 1, можно сделать вывод, что универсальный финитно-временной оптимальный метод фильтрации и прогнозирования навигационных дискретных сигналов при выбранном значении объема памяти по точности незначительно отличается от фильтрации Калмана и метода прогноза на его основе.
Финитно-временная оценка прогноза при выбранном значении объема памяти также показала несущественно отличающиеся от прогноза Калмана результаты как по точности, так и по времени переходного процесса.
На рисунках 4, 5 представлено изменение значений дисперсии ошибки оценки финитно-временной фильтрации и прогнозирования при изменении параметра – объема памяти. Как мы видим, с ростом объема памяти дисперсия ошибки оценки финитно-временной фильтрации и прогнозирования стремится к дисперсиям фильтрации Калмана и его методу прогнозу. При
= 6 отличий практически нет. Обозначения на рисунках следующие:
– для рисунка 4: и
– статистические значения дисперсий ошибки оценки финитно-временной обработки и фильтрации Калмана соответственно;
– для рисунка 5: и
– статистические значения дисперсий ошибки оценки финитно-временной оценки прогноза и прогноза методом Калмана соответственно.
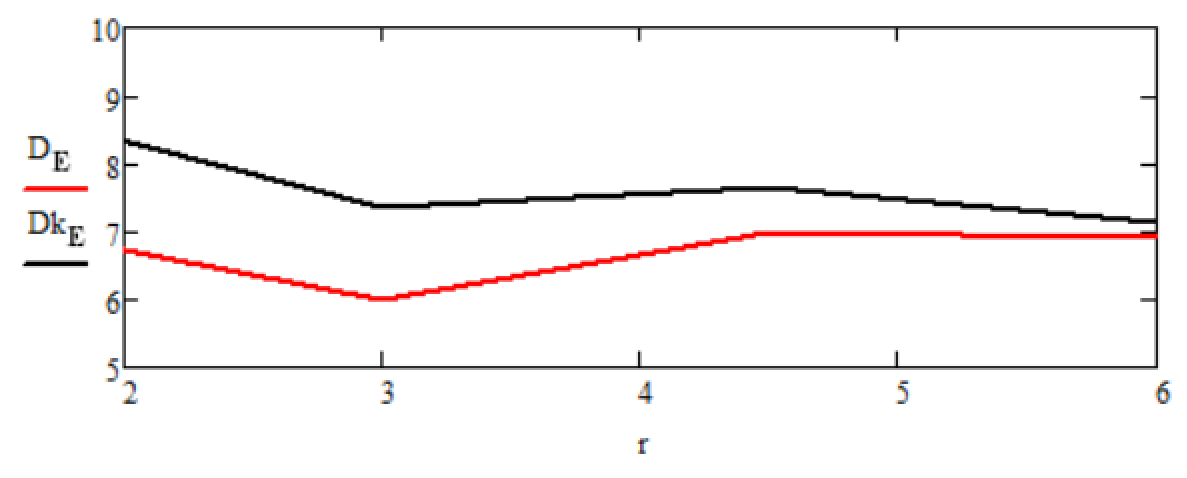
Рисунок 4 - Графики зависимостей статистических дисперсий ошибок оценок финитно-временной обработки и фильтрации Калмана от изменения параметра r на интервале от 2 до 6
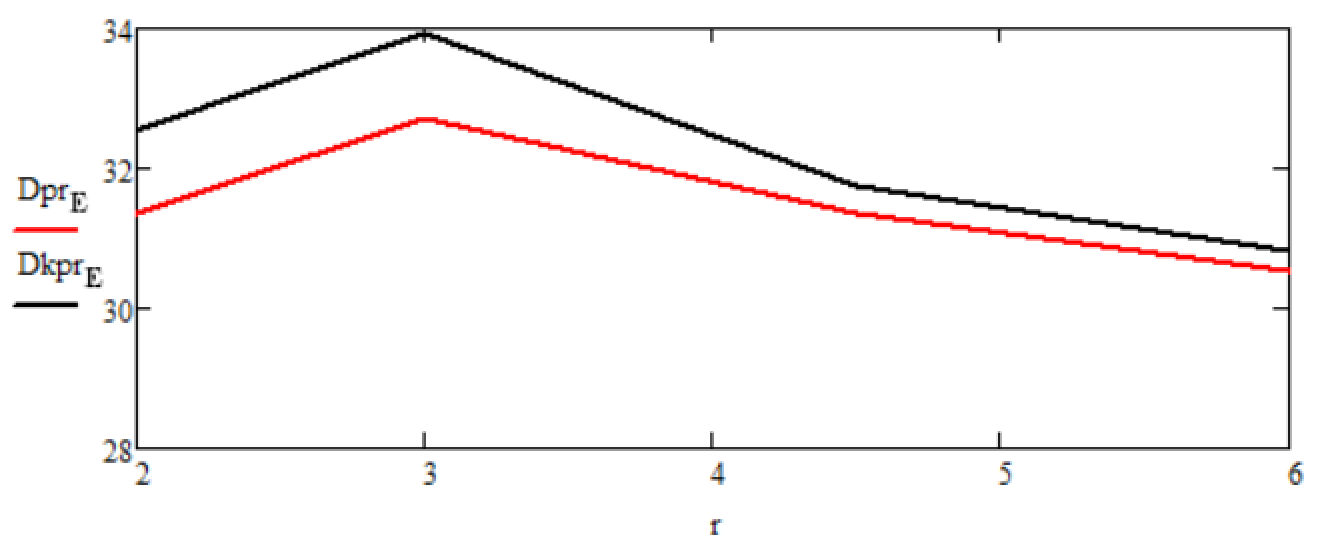
Рисунок 5 - Графики зависимостей статистических дисперсий ошибок оценок финитно-временной оценки прогноза и прогноза Калмана от изменения параметра r на интервале от 2 до 6 при времени прогноза T = 10 с
Посмотрим как изменяется дисперсия ошибки оценки финитно-временного прогнозирования и прогноза Калмана при изменении интервала времени прогноза (рисунок 6). Обозначения на рисунке следующие: и
– статистические значения дисперсий ошибки оценки финитно-временной оценки прогноза и прогноза метода Калмана соответственно.
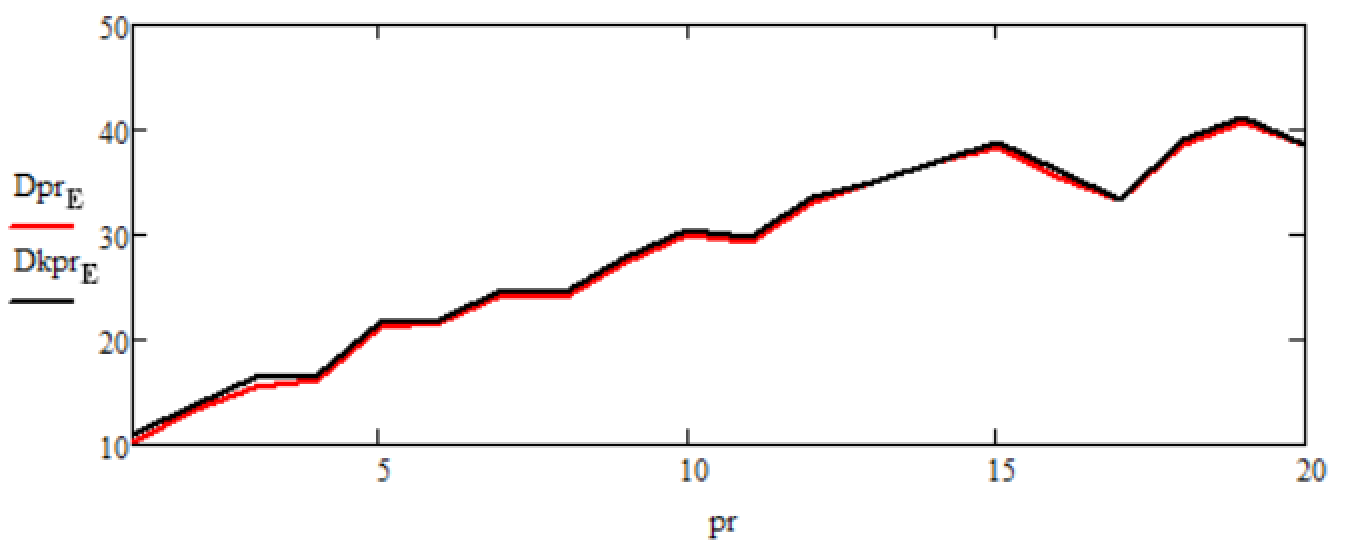
Рисунок 6 - Графики зависимостей статистических дисперсий ошибок оценок финитно-временной оценки прогноза и прогноза фильтра Калмана от изменения параметра T на интервале от 0 до 20
Робастность представляет собой устойчивость характеристик точности при изменении параметров обработки сигнала. Показатель робастности определяется формулой :
где – изменение показателя качества системы при отклонении рассматриваемого параметра от номинального значения на величину
;
– показатель качества системы при номинальном значении параметра;
– номинальное значение рассматриваемого параметра системы.
Помехозащищенность представляет собой устойчивость характеристик точности системы при изменении параметров входных сигналов. Критерий показателя помехозащищенности определяется следующим образом :
где – изменение показателя качества системы при отклонении рассматриваемого параметра от номинального значения на величину
;
– показатель качества системы при номинальном значении параметров помехи;
– номинальное значение рассматриваемого параметра помехи.
Обозначения на рисунках следующие:
– для рисунков 7, 9, 11, 13: и
– статистические значения дисперсий ошибки оценкифинитно-временной обработки и фильтрации Калмана соответственно;
– для рисунков 8, 10, 12, 14: и
– статистические значения дисперсий ошибки оценкифинитно-временной оценки прогноза и прогноза Калмана соответственно.
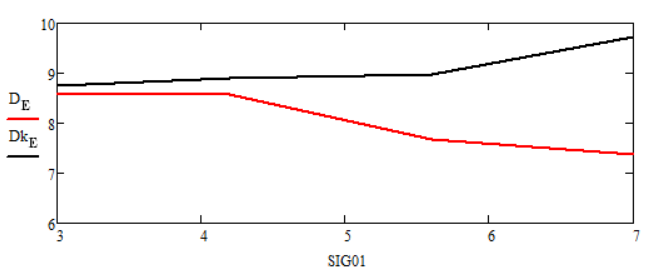
Рисунок 7 - Графики зависимостей статистических дисперсий ошибок оценок финитно-временной обработки и фильтрации Калмана от изменения среднеквадратического отклонения помехи σH на интервале от 3 до 7
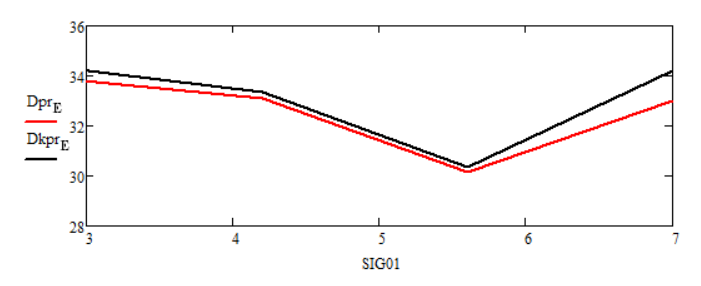
Рисунок 8 - Графики зависимостей статистических дисперсий ошибок оценок финитно-временной оценки прогноза и прогнозирования Калмана от изменения среднеквадратического отклонения помехи σH на интервале от 3 до 7 при времени прогноза T = 10 с
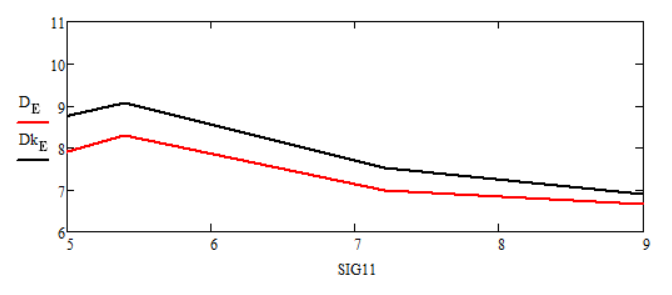
Рисунок 9 - Графики зависимостей статистических дисперсий ошибок оценок финитно-временной обработки и фильтра Калмана от изменения среднеквадратического отклонения полезного сигнала σ на интервале от 5 до 9
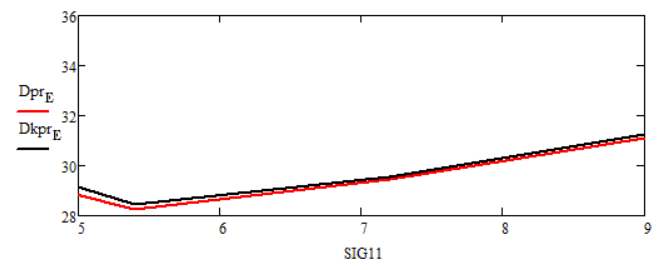
Рисунок 10 - Графики зависимостей статистических дисперсий ошибок оценок финитно-временной оценки прогноза и прогноза фильтра Калмана от изменения среднеквадратического отклонения полезного сигнала σ на интервале от 5 до 9 при времени прогноза T = 10 с
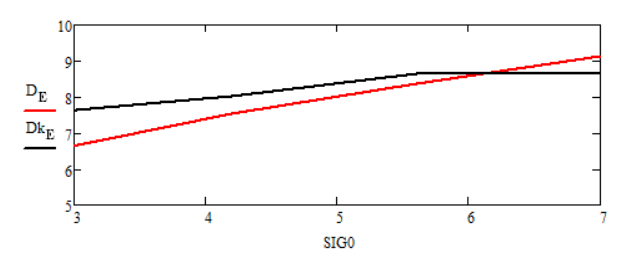
Рисунок 11 - Графики зависимостей статистических дисперсий ошибок оценок финитно-временной обработки и фильтрации Калмана от изменения среднеквадратического отклонения помехи σH на интервале от 3 до 7
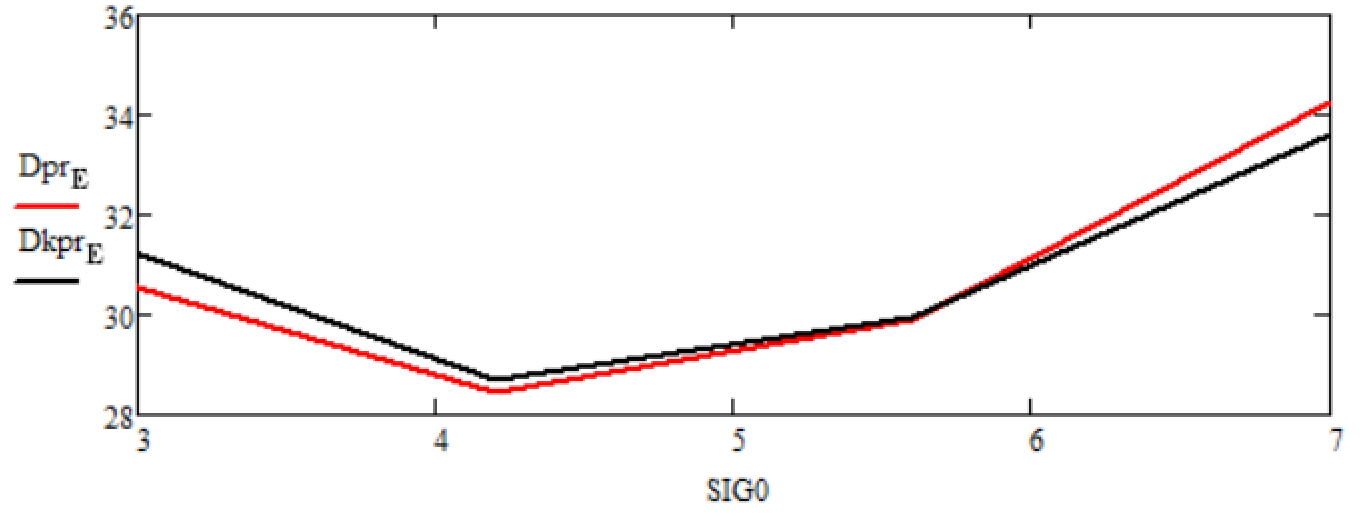
Рисунок 12 - Графики зависимостей статистических дисперсий ошибок оценок финитно-временной оценки прогноза и прогнозирования Калмана от изменения среднеквадратического отклонения помехи σH на интервале от 3 до 7 при времени прогноза T = 10 с
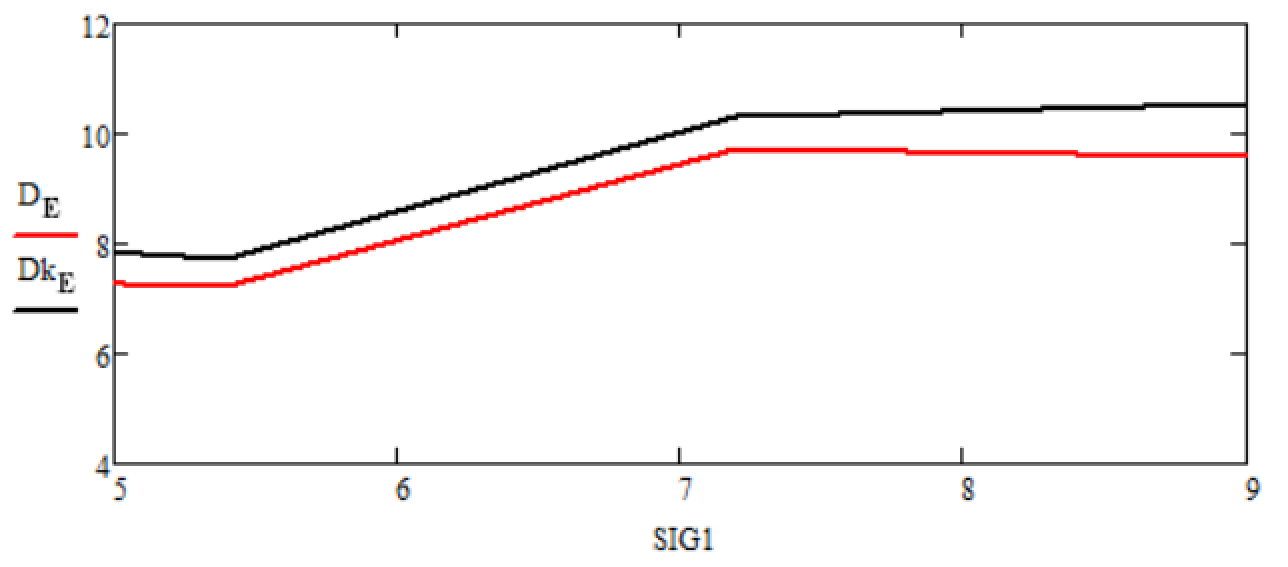
Рисунок 13 - Графики зависимостей статистических дисперсий ошибок оценок финитно-временной обработки и фильтра Калмана от изменения среднеквадратического отклонения полезного сигнала σ на интервале от 5 до 9
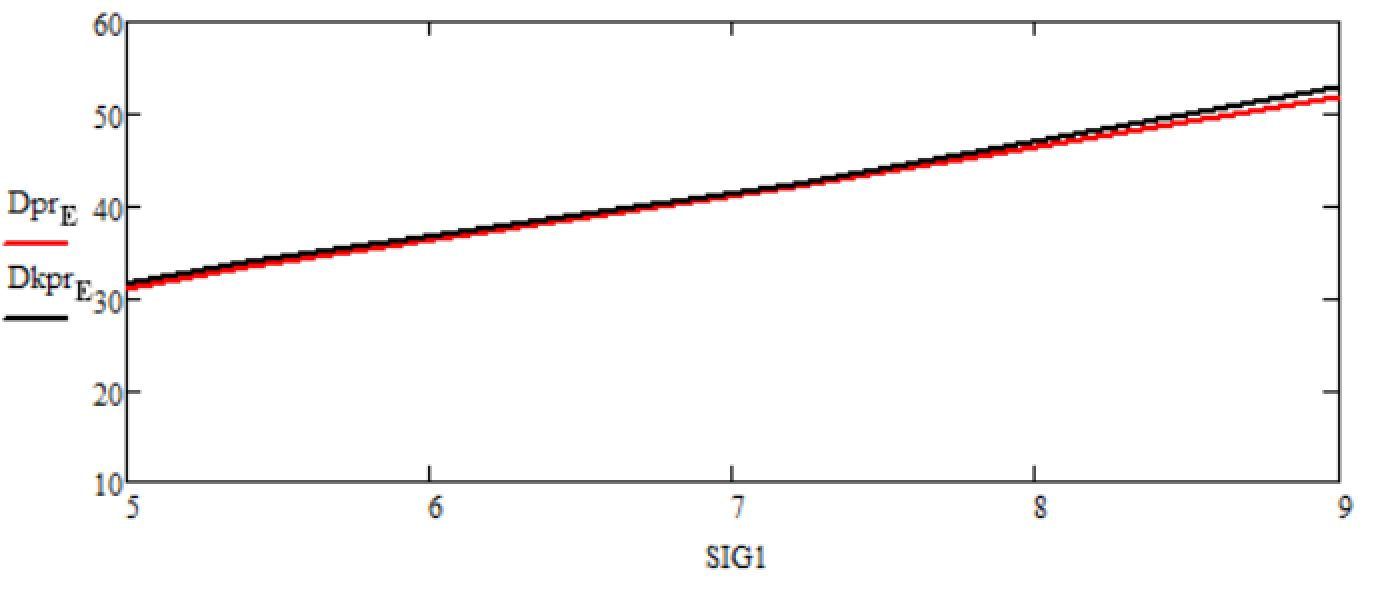
Рисунок 14 - Графики зависимостей статистических дисперсий ошибок оценок финитно-временной оценки прогноза и прогноза фильтра Калмана от изменения среднеквадратического отклонения полезного сигнала σ на интервале от 5 до 9 при времени прогноза T = 10 с
По рисункам 7-10 можно сделать следующие выводы:
– при изменении среднеквадратического отклонения помехи фильтрация Калмана является более робастной в сравнении с финитно-временной обработкой (рисунок 7). В случае прогноза (рисунок 8) оба метода показали практически одинаковые результаты;
– при изменении среднеквадратического отклонения полезного сигнала (рисунки 9, 10) финитно-временной метод обработки и прогнозирования показал аналогичную робастность фильтрации и прогноза Калмана.
По рисункам 11-14 можно сделать следующие выводы:
– при изменении среднеквадратического отклонения помехи в сравнении с финитно-временной обработкой, фильтрация Калмана показала наибольшую устойчивость (рисунок 11). В случае прогноза (рисунок 12), помехозащищенность обоих методов сравнима друг с другом;
– при изменении среднеквадратического отклонения полезного сигнала (рисунки 13, 14) помехозащищенность финитно-временного метода обработки и прогнозирования аналогична значениям фильтрации и прогнозу Калмана.
4. Заключение
Рассматриваемый в рамках исследования универсальный финитно-временной оптимальный метод обработки и прогнозирования навигационных дискретных сигналов предлагается в качестве альтернативы фильтрации и прогнозированию Калмана. Новый метод обработки отличается простотой реализации и универсальностью в плане вида используемых моделей сигнала, он инвариантен к наличию или отсутствию коррелированности помехи измерения и не требует от процессов наличия свойства марковости. По результатам сравнительного анализа двух методов можно сказать, что финитно-временная обработка не уступает фильтрации Калмана по точности и времени переходного процесса. При этом с ростом объема памяти , точность финитно-временной обработки будет асимптотически стремиться к значениям точности фильтрации Калмана. Финитно-временной метод прогноза навигационных сигналов также включает в себя преимущества обработки, а по точности, времени переходного процесса и простоте реализации практически не отличим от прогнозирования Калмана. К недостаткам рассматриваемого алгоритма можно отнести наличие требования в накоплении памяти процесса
начальных данных, в ходе которого возникает априорная неопределенность, устраняемая при оценке точности алгоритма с течением времени.
По показателям робастности и помехозащищенности, финитно-временной метод обработки и прогнозирования уступает фильтрации и методу прогнозу Калману лишь при изменении среднеквадратического отклонения помехи . В остальных случаях были получены сравнительные с Калманом результаты.
