A DIGITAL APPROACH OF HYSTERESIS LOOP ANALYSIS ON THE EXAMPLE OF CIRCULATORY SYSTEM RESPONSE UNDER CONDITIONS OF COGNITIVE LOAD IN STUDENTS
A DIGITAL APPROACH OF HYSTERESIS LOOP ANALYSIS ON THE EXAMPLE OF CIRCULATORY SYSTEM RESPONSE UNDER CONDITIONS OF COGNITIVE LOAD IN STUDENTS
Abstract
Digital analysis of the hysteresis loop complements its qualitative characteristics, which allows to unify the obtained data of clinical and physiological tests of human condition evaluation. The aim of the study is to substantiate and develop a method of hysteresis loop digitization on the example of the circulatory system reaction under conditions of cognitive load in students. 35 people were examined (18 – boys, 17 – girls), all participants were second-year students of a medical university, average age 19±0.07 years. Subjects' pulse pressure and heart rate (HR) were determined in hyperloop conditions – baseline – cognitive load (Amthauer test) – recovery after load. The hysteresis loop criteria we introduced: Stress, PhT– phase transition state, change of regulatory mechanisms providing adaptation at the moment of load, RR – recovery reaction after load, RV – recovery vector, Set point – level of non-equilibrium, phase transition point, SD1 – state disequilibrium, activation of regulation mechanisms to stress, SD2 – disequilibrium state – change of regulation mechanisms during recovery, as well as the developed method of digital analysis of these criteria substantiate the following conclusions. The digital approach of hysteresis loop analysis allows to quantitatively evaluate variants of the relationship between the states of tension and recovery during the performance of stress tests. The Set point, being the basis of the phase transition, determines the efficiency and direction of the recovery reaction.
1. Введение
Многие физиологические и патологические процессы организма характеризуются цикличностью, т.е. последовательной сменой фаз. Такую цикличность можно проследить как в условиях реализации классической стресс-реакции, так и в реализации физиологических процессов, направленных на поддержание гомеостаза в целом. Для этих процессов характерна фазовость реакции, направленная на поддержание определенной функции в физиологическом диапазоне. Естественно, что колебательный характер определенной функции проявляется не только классическим вариантом реагирования, принятого выражать как +/-, но и уровнем фазового перехода, т.е. состоянием неравновесности. Так, в частности, для состояния стресса характерна достаточно четкая стадийность процесса: – тревога – резистентность – восстановление
, , причем стадия восстановления зависит от интенсивности стрессора и адаптационных ресурсов организма. Именно поэтому понимание механизмов и вариантов «выхода» организма из стресса является частным вариантом наиболее фундаментальной закономерности, связанной с регуляцией гомеостатических констант организма в целом, в условиях нормы и патологии. Варианты «выходов» из состояния стресса могут быть различными и интерпретироваться как отсроченная «плата» за стресс , . По нашему мнению, реакция восстановления лимитирует исходы стресса и наиболее уязвима за счет многообразия вариантов восстановления. Значимость этой реакции можно хорошо проиллюстрировать на деятельности сердца – когда эффективность систолы закладывается в диастоле, известный термин «диастолическая дисфункция», в клиническом аспекте, рассматривается как прелюдия более глубоких нарушений сердечной деятельности в перспективе . Следовательно, процесс напряжения (стресс) и реакцию восстановления, необходимо рассматривать как единый гиперцикл, в основе которого лежат системные изменения активности регуляторных контуров, базирующиеся на взаимоотношениях между симпатической и парасимпатической нервными системами. Этот баланс, либо дисбаланс, поддерживаются на различном уровне неравновесности. Явление гистерезиса, как ранее нами показано , , позволяет выявить особенности межсистемных отношений в целом и регуляцию работы сердца в частности. На предыдущем этапе исследования анализ петли гистерезиса основывался в основном на ее качественных особенностях . В настоящей работе поставлена задача разработки методов по цифровому анализу петли гистерезиса на примере колебательных процессов сила-частота сердечных сокращений в условиях цикла – состояние покоя-когнитивная нагрузка-восстановление после нагрузки. Полагаем, что на современном этапе осмысление значимости оценки петли гистерезиса, как в условиях нормы, так и патологии, позволит унифицировать полученные данные, дополнив, тем самым, клинико-физиологические методы оценки состояния человека. Таким образом, разработка и обоснование цифрового подхода при анализе петли гистерезиса определили цели и задачи настоящего исследования.Цель исследования: обосновать и разработать методику оцифровки петли гистерезиса на примере реакции системы кровообращения в условиях когнитивной нагрузки у студентов.
Задачи исследования:
1. Цифровой анализ петли гистерезиса в оценке системы кровообращения в условиях когнитивной нагрузки в обследуемых группах.
2. Оценка фазовых переходов на основе распределения точек Setpoint с применением петли гистерезиса.
2. Методы и принципы исследования
В исследовании приняли участие 35 человек из них – 18 юношей, средний возраст 19,4±0,1 лет, 17 девушек, средний возраст 19,0±0,05 лет, все участники студенты второго курса, педиатрического факультета медицинского университета г. Новосибирска. Исследование проводилось весной. В качестве нагрузки применялся тест Амтхауэра (устное решение арифметических задач) . В ходе исследования регистрировалось артериальное давление (АД), после чего определялось, пульсовое давление (ПД) в мм.рт.ст. Измерялась частота сердечных сокращений (ЧСС) – уд/мин. Осуществлялось 4 замера – ПД, ЧСС – 1 – до проведения исследования, ПД, ЧСС – 2 – вовремя исследования, ПД, ЧСС – 3 – сразу после проведения исследования, ПД, ЧСС – 4 – через 5 минут после проведения исследования . Полученные результаты обрабатывались с использованием пакета прикладных программ: Exel-7.0, Advanced Grapher и Statistika-7,0. Для обработки полученных данных использовались непараметрические методы анализа для зависимых и независимых переменных. Различия считались достоверными при р < 0,05. При M – показатель средних величин, m – ошибка средней величины. Различия считались достоверными при р < 0,05.
3. Основные результаты
На первом этапе нашего исследования мы оценили показатели ПД, и ЧСС в общей группе обследуемых, в группах юношей и девушек в 4-х измерениях (табл.1,2), и проследили динамику зависимости этих показателей относительно друг друга с применением явления гистерезиса (рис. 1,2,3). Юноши и девушки одного возраста 19±0,07 лет, в группе девушек фаза менструального цикла не учитывалась.
Таблица 1 - Значения пульсового давления и частоты сердечных сокращений в четырех точках измерений в общей группе обследуемых
Параметр | ПД-1, мм.рт.ст | ПД-2, мм.рт.ст | ПД-3, мм.рт.ст | ПД-4, мм.рт.ст | ЧСС-1, уд/мин | ЧСС-2, уд/мин | ЧСС-3, уд/мин | ЧСС-4, уд/мин |
Общая группа | 40,2±1,8 | 40,0±2,2 | 42,0±2,2 | 39,7±1,5 | 77,2±1,6 | 90,4±2,4٭ | 87,3±2,0٭ | 78,1±1,8 |
Примечание: M±m; ПД – пульсовое давление; ЧСС – частота сердечных сокращений; 1,2,3,4 – замер исследования; ٭ - достоверное отличие; р < 0,05
Для построения петли гистерезиса учитывали одновременно показатели ЧСС и ПД в четырех точках исследования в системе координат х и у. Для анализа петли гистерезиса мы предлагаем вариант оцифровки показателей. Для оцифровки использовался графический модуль программы Exel, с применением масштабной сетки, где сторона малого квадрата составляет 2 см, что составляет 75,87 пикселей (px). Конвертация сантиметров в пиксели осуществлялась с использованием онлайн конвертера сантиметров в пиксели
. Конвертация необходима для стандартизации получаемых значений.Для оцифровки показателей нами введены критерии (рис.1):
- Stress – отрезок 1-2 петли гистерезиса, который отражает переход регуляторных механизмов системы кровообращения от исходного состояния к пику выполнения нагрузки.
- PhT – phase transition – отрезок 2-3 (пик нагрузки – завершение нагрузки), переходное состояние, т.е. смена регуляторных механизмов, обеспечивающих адаптацию в момент нагрузки.
- RR – recoveryreaction – отрезок 3-4 (реакция восстановления после выполнения нагрузки), переходное состояние, характеризует смену механизмов регуляции в процессе восстановления.
- RV – recovery vector – вектор С (1-4) – направление реакции восстановления.
- Точка Setpoint – уровень неравновесности, точка фазового перехода. Рассчитывается, как сумма всех показателей, деленная на их количество. Точка Setpoint отражает определенную точку в виртуальном пространстве, где происходит инверсия программ регуляции и закладывается вектор процессов восстановления.
- SD1 – state disequilibrium 1 – вектор А (1 – точка Setpoint), состояние неравновесности 1, включение механизмов регуляции на стресс.
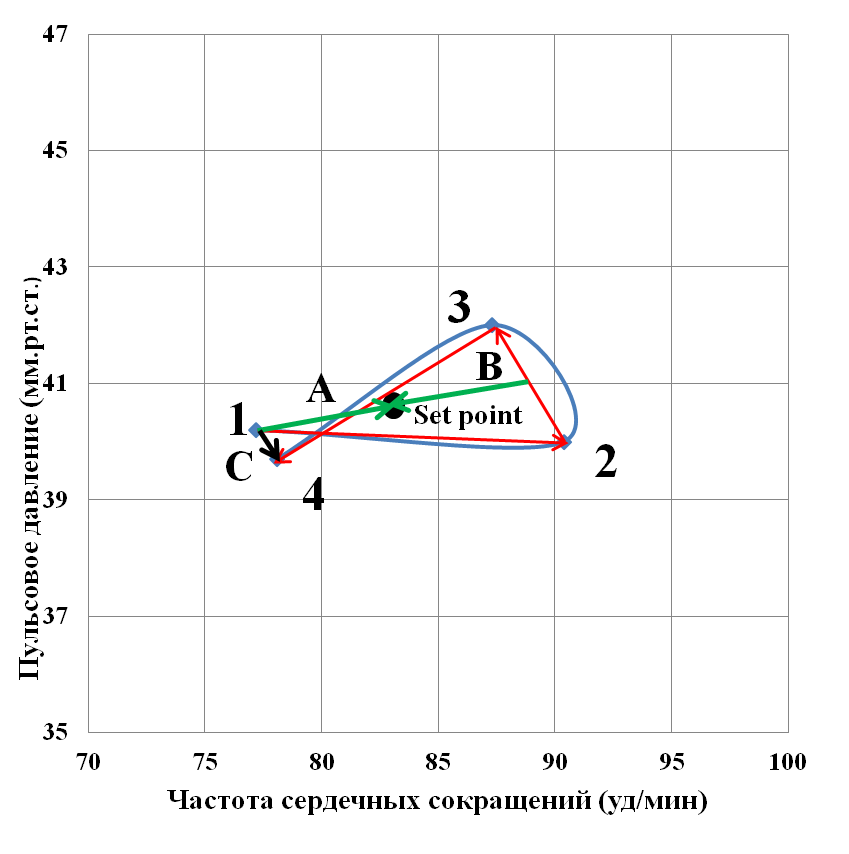
Рисунок 1 - Динамика ПД и ЧСС в четырех точках исследования в общей группе обследуемых
Отрезок 1-2 (Stress) составляет – 199,93 px. Отрезок 2-3 (PhT) – 73,22 px, отрезок 3-4 (RR) – 142,64 px. Вектор С (RV) – 20,1px. RV – направлен вниз, т.е. показатели ЧСС и ПД после восстановления меньше исходных величин, это реакция гипервосстановления. SD1 – 88,39px. SD2 – 90,29px.
Таблица 2 - Значения пульсового давления и частоты сердечных сокращений в четырех точках измерений в группах обследуемых юношей и девушек
Параметр | Юноши | Девушки | Достоверность |
ПД-1, мм.рт.ст | 44,4±2,3 | 35,8±2,4 | р=0,01 |
ПД-2, мм.рт.ст | 44,4±2,5 | 39,4±3,6 | - |
ПД-3, мм.рт.ст | 46,6±2,8٭ | 37,0±3,2 | р=0,03 |
ПД-4, мм.рт.ст | 40,5±2,4٭ | 38,8±1,8 | - |
ЧСС-1, уд/мин | 77,0±2,2 | 77,4±2,4 | - |
ЧСС-2, уд/мин | 86,0±3,1٭ | 94,2±3,4٭ | - |
ЧСС-3, уд/мин | 84,5±2,6٭ | 89,8±3,0٭ | - |
ЧСС-4, уд/мин | 77,0±2,1٭ | 79,1±3,0٭ | - |
Примечание: M±m; ПД – пульсовое давление; ЧСС – частота сердечных сокращений; 1,2,3,4 – замер исследования; ٭ - достоверное отличие в группах юношей и девушек (по вертикали); р < 0,05
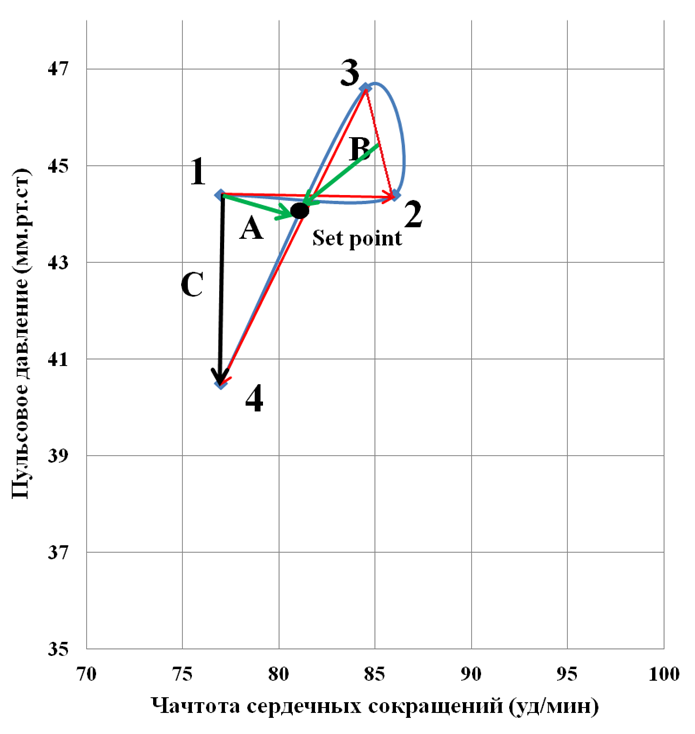
Рисунок 2 - Динамика ПД и ЧСС в четырех точках исследования группе юношей
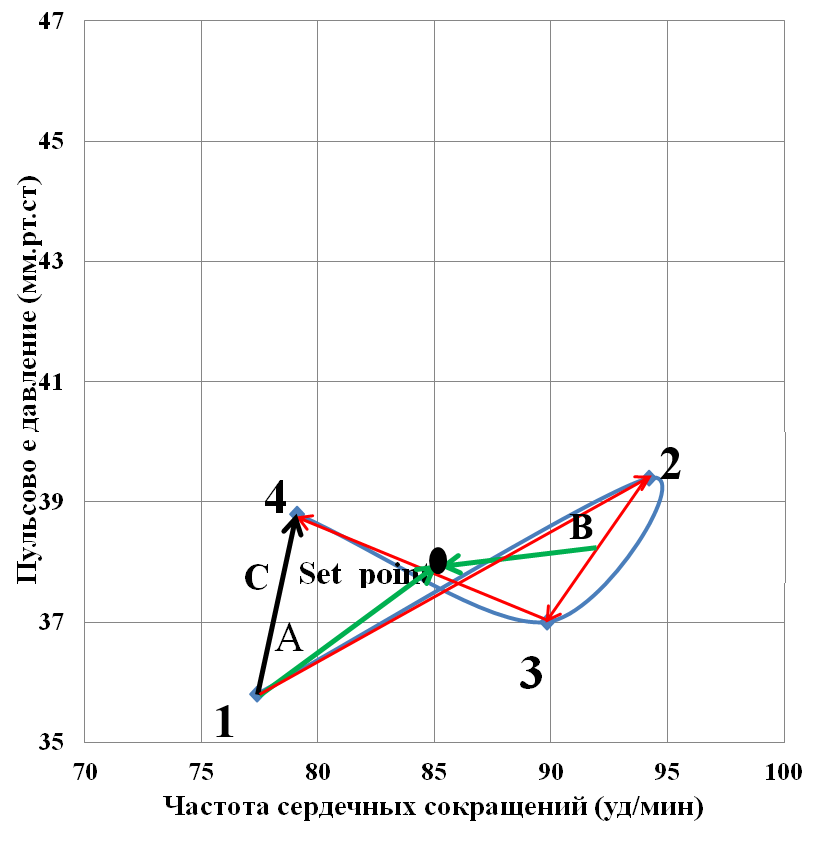
Рисунок 3 - Динамика ПД и ЧСС в четырех точках исследования группе девушек
Отрезок 1-2 (Stress) составляет – 251,9 px. Отрезок 2-3 (PhT) – 93,32 px, отрезок 3-4 (RR) – 162,75 px. Вектор С (RV) – 116,46 px. RV – направлен вверх, т.е. показатели ЧСС и ПД после восстановления меньше исходных величин, это реакция гиповосстановления. В точке восстановления ЧСС возвращается к исходному уровню. Показатель ПД снижается. SD1 –114,57 px. SD2 – 101,29 px. С целью сравнительной оценки полученных результатов во всех обследованных группах они систематизированы в таблице 4.
Таблица 3 - Оцифрованные значения показателей петли гистерезиса в пикселях в группах обследуемых
| Stress | PhT | RR | RV | SD1 | SD 2 |
Общая группа | 199,93 | 73,22 | 142,64 | 20,1(-) | 88,39 | 90,29 |
Группа юношей | 135,43 | 84,22 | 231,04 | 149,47 (-) | 55,38 | 69,42 |
Группа девушек | 251,9 | 93,32 | 162,75 | 116,46 (+) | 114,57 | 101,29 |
Примечание: «-» - направление вектора вниз; «+» - направление вектора вверх
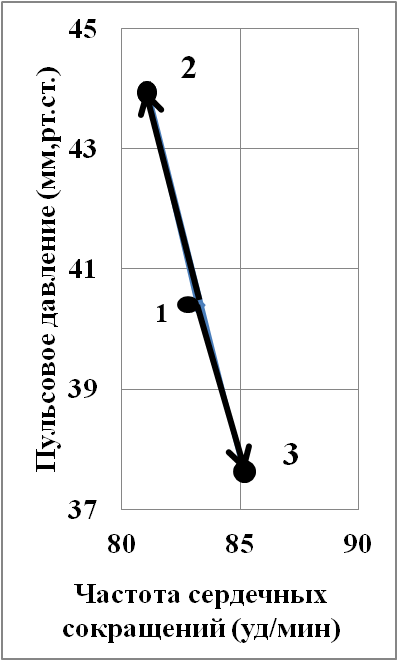
Рисунок 4 - Динамика точки Set point в группах обследуемых:
1 – общая группа; 2 – группа юношей; 3 – группа девушек
4. Обсуждение результатов исследования
Когнитивная нагрузка, применяемая в нашем исследовании, в качестве нагрузочного теста, является стимулирующим и стрессирующим фактором, влияние которого проявляется особенностями регуляции системы кровообращения. В исследованиях выявлена жесткая связь когнитивных процессов с динамикой вегетативной регуляции работы сердца посредствам общей нейрофизиологической основы. В развитии стресс-реакции стадия восстановления намного продолжительнее и разнообразнее стресс-реагирования. Эта стадия не детерминирована и не имеет конкретного стимула. Процесс переключения стресса на реакцию восстановления формируется в рамках фазовых переходов, когда, в результате дестабилизации функции «выбирается» стратегия восстановительного процесса и закладывается его вариант. В качестве методического подхода в оценке реакции восстановления предлагается использовать явление гистерезиса. Введенные нами критерии петли гистерезиса и их оцифровка позволяют количественно оценить варианты реакции восстановления (RR), и определить вектор восстановления (RV). В группе юношей реакция восстановления более продолжительная, в отличие от группы девушек, а вектор восстановления направлен вниз – реакция гипервосстановления, у девушек вектор восстановления направлен вверх – гиповосстановление. При проведении когнитивной нагрузки регуляторный контур АД представляет собой структуру переходных процессов имеющих нелинейный характер . Показатель уровня неравновесности системы – точка Set point, является средней величиной от исследуемых показателей, она определяет уровень структуры, формирующей реакцию восстановления. Цифровой подход анализа петли гистерезиса выявляет точку Set point и позволяет провести сравнительную характеристику SD1 и SD2. В группе юношей соотношение напряжение/восстановление определяет преобладание реакции восстановления. В группе девушек такой закономерности нет. Мы предполагаем, что существует взаимосвязь между точкой Set point и характером фазового перехода регуляторных механизмов, а также структурой реакции восстановления. Чем больше величина неравновесности (Set point), тем раньше и быстрее наступает фазовый переход, а восстановление осуществляется по «мономодальному» – т.е эффективному варианту, в нашем исследовании, это группа юношей. Чем меньше уровень неравновесности (Set point), фазовый переход замедляется, и восстановление идет по «мультимодальному» варианту – неэффективный вариант, в нашем исследовании, группа девушек. «Мономодальный» вариант восстановления характеризуется наличием предопределенных причинно-следственных отношений между взаимодействующими регуляторными системами. «Мультимодальный» вариант восстановления определяется стохастическим принципом межсистемных отношений. Этот вариант более чувствителен к различным воздействиям и факторам, что может проявляться нарушениями функций на этапе реакции восстановления.
5. Заключение
1. Цифровой подход анализа петли гистерезиса позволяет количественно оценить варианты соотношения между состояниями напряжения и восстановления при выполнении клинико-физиологических нагрузочных тестов. Оцифровка и унификация показателей петли гистерезиса обеспечивает объективный обмен информацией и создает условия для выявления и разработки новых диагностических и прогностических критериев.
2. Точка Setpoint характеризует взаимосвязь между уровнем неравновесности и структурой регуляторных механизмов ответственных за адаптацию в условиях нагрузочного теста, являясь основой фазового перехода, что определяет эффективность и направление реакции восстановления.
