Об одном наглядном описании исторического события с помощью тригонометрического уравнения и его решения
Об одном наглядном описании исторического события с помощью тригонометрического уравнения и его решения
Аннотация
В данной статье предпринята попытка анализа исторических событий методами математики, причем средствами, не выходящими за рамки школьной программы. Моделируется процесс нашествия джунгар 1643-1745г.г. с помощью тригонометрического уравнения. Строится графики характеристических функции джунгарского государства и казахского народа. Формулируется теорема (критерий) для решения поставленной задачи.
Представляется, что данный подход будет интересен не только с исторической и математической точек зрения, но и позволит заинтересовать учащихся к изучению как истории, так и математики, обогатит методику преподавания данных дисциплин в средней школе, позволит обосновать междисциплинарную связь математики и истории.
1. Введение
Математическим моделированием биологических, социально-исторических и этнических процессов занимались такие ученые как В.И. Арнольд, Ю.Е. Аниконов, В. Вальтерра, А.М. Нахушев, Р.О. Кенетова
, , , , .В. Вальтерра в своей работе
описывается исследования, включающие проявления борьбы между членами некоторого сообщества, прирост одних благодаря гибели других. Математический подход опирается на изучение решений некоторых дифференциальных и интегро-дифференциальных уравнений, поведение которых нужно детально исследовать, либо, количественно, либо, чаще, только качественно. Работы А.М. Нахушева и Р.О. Кенетовой , , , посвящены математическому моделированию нелокальных процессов в сложных системах, моделированию социально-исторических и этнических процессов, протекающих на уровне национальных сообществ, этнических социумов, нередко определяющимися наличием очагов конфликтности.Изучая исторические данные, многие исследователи в области философии, антропологии, генетики, теологии, археологии пытаются найти фундаментальное объяснение историческому процессу. Иными словами, мы можем считать, что предмет истории имеет отношение и к названным наукам. Исходя из определений теории познания, мы знаем, что неполное знание об исследуемом объекте называют относительной истиной, а полное знание и точную информацию – абсолютной истиной. Относительная истина и абсолютная истина суть моменты проявления объективной реальности как общественно-исторического процесса. Объективная реальность существует только в относительно-абсолютной форме
.Таким образом, зачастую бывает недостаточным изучать историю, исходя лишь из ее собственных факторов: географической среды, территориальным и этническим границам, политико-социальным особенностям, экономического уклада, религии. Если рассматривать историю казахского народа на определенных этапах, то ее, на первый взгляд, достаточно сложно классифицировать и привести к единой системе. Так, анализ истории гуннов, саков, уйсинов (3 в. до н.э. – 3 в. до н.э.), огидов и киданов (8-9 вв.), монголов (12-14 вв.) не объясняет, даже с точки зрения профессиональных историков, причин вражды между казахами и джунгарами, особенностей военной стратегии и тактики со стороны поздних джунгар (17-18 вв.).
Следует отметить, что, по мнению Л.Н. Гумилева, ученые и исследователи избегают географического детерминизма, т. е. уклоняются от оценки влияния окружающей среды, климата и т. п. на судьбы общества и цивилизации, иными словами, склонны к географическому нигилизму, даже не замечая, что значение природной среды вообще не учитывается
.При этом территория Казахстана по физико-географической характеристике состоит из трех основных частей
. Западный, Северо-Западный Казахстан – пустыни, низменные степи; Северный и Центральный Казахстан – степные, луговые, горные; Южный, юго-восточный Казахстан имеет реки и озера, пастбища и горы. Подобные этнотерриториальные данные, в том числе, позволяют перейти к использованию описания исторических исследований математическими методами.Отметим работу
доктора исторических наук, профессора Талгата Абдразакова «О нашествии джунгаров с 1643 по 1745 г.г. и его социально-экономические корни», в которой приведено обоснование длительной вражды между казахами и джунгарами.В настоящей работе предпринята попытка анализа исторических событий методами математики, причем средствами, не выходящими за рамки школьной программы. Представляется, что данный подход будет интересен не только с исторической и математической точек зрения, но и позволит заинтересовать учащихся к изучению как истории, так и математики, обогатит методику преподавания данных дисциплин в средней школе, позволит обосновать междисциплинарную связь математики и истории.
2. Применяемые вспомогательные математические понятия
Понятие Теорема в математике означает, что свойство, удовлетворяющее определенному условию А, порождает свойство, удовлетворяющее условию В
.Критерий – это необходимое и достаточное условие.
1. Некоторые исследователи считают, что на политику руководства Джунгарского государства оказало влияние стремление Чингисхана создать огромную империю.
2. Если согласится с приведенным в пункте (1) утверждением, то придем к выводу, что джунгары, потерявшие территории в результате поражения от Китайской империи Цинь, стремились компенсировать потерянные территории за счёт территории Казахстана.
Перейдем к обоснованию математической модели.
Характеристическую функцию Джунгарского государства, включающую психологические, природные, социально-экономические, этнические, демографические, территориальные параметры, представим в следующем виде:
Аналогично построим характерическую функцию казахского народа:
Если внимательно изучить исторические основы, этапы и предпосылки войн между любыми двумя государствами, двумя народами, можно наблюдать следующий закономерный характерный процесс. Практически всегда войны возникают при таком отклонении основных параметров от состояния покоя, которые приводят к антагонистическим противоречиям.
Рассмотрим сбалансированное состояние функций двух государств, характерное для исторических факторов социально-экономического исторического развития и периодов упадка. Причина создания уравнения будет видна в ходе работы.
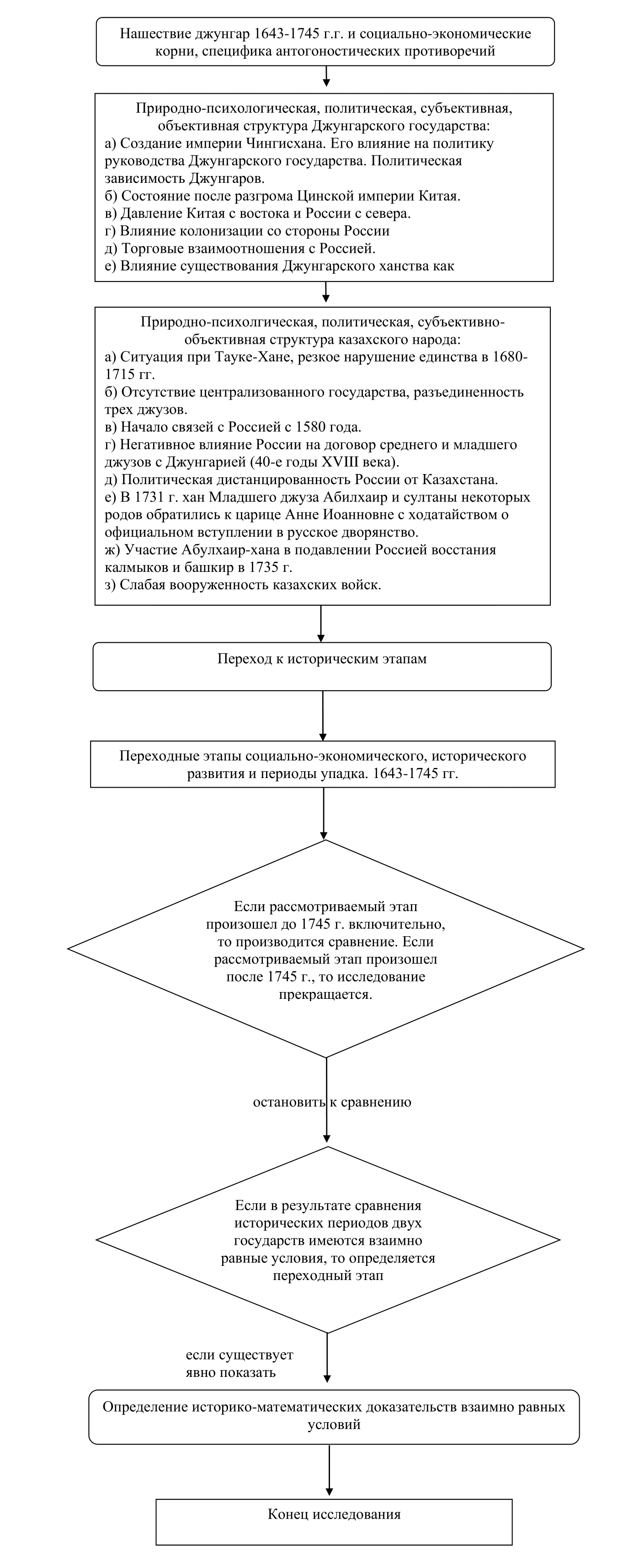
Рисунок 1 - Cтруктурная схема
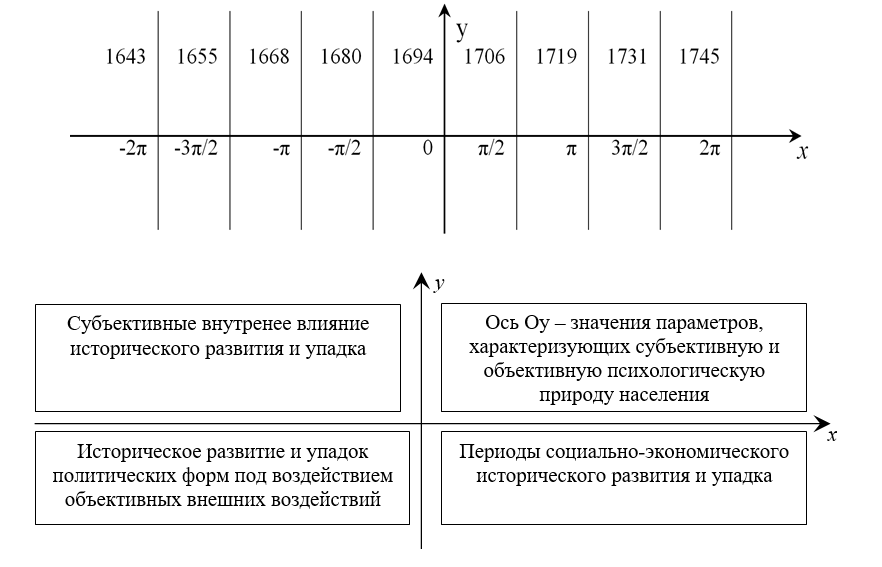
Рисунок 2 - Ввод декартовых координат
Построим график характеристической функции джунгарского государства.
3. Аналитический и графический методы решения
Рассмотрим график функции
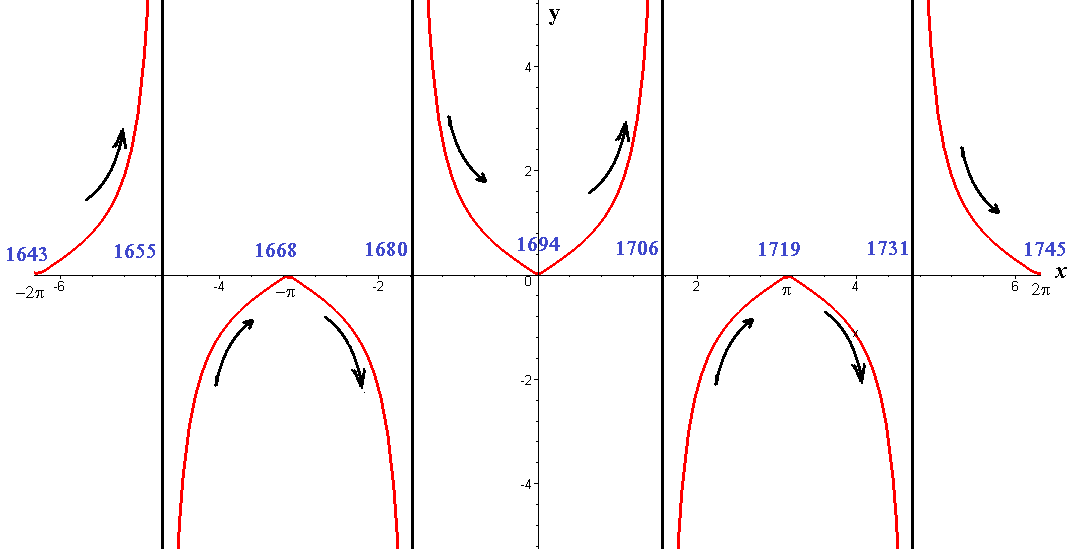
Рисунок 3 - График функции (1)
В период 1643-1655гг. это было психологически, эмоционально, субъективно развитое государство с сильной готовностью к войне.
В 1655-1668 годах под влиянием внешнеполитических форм она развивалась в соответствии с объективными факторами.
С 1668 по 1680 год оно объективно пришло в упадок под влиянием конфликта с империей Цинь.
С 1668 по 1694г., а также в период 1681-1684г. за счет войны с казахскими джузами произошел субъективный упадок.
В 1694 году произошло антогоностическое противоречие. В 1694-1705г.г. стычка Цэбдан Рабдана с Таукеханом привела к субъективному росту.
В период 1706-1719г.г., функция определяется объективно, в связи с внешнеполитическим влиянием вооруженных конфликтов с Казахским ханством в 1717 году.
В период 1719-1731г.г., 1727-1730г.г. казахские войска нанесли джунгарам ощутимое поражение, что привело к объективному упадку.
В период 1731-1745гг. воздействие таких ударов ослабило психологическую систему джунгарского народа в целом, произошел субъективный упадок. В 1745 году внутриполитическая обстановка в Джунгарии обострилась. Заметим, что различий в значениях параметров, характерных для субъективной и объективной психологической природы джунгар, не было.
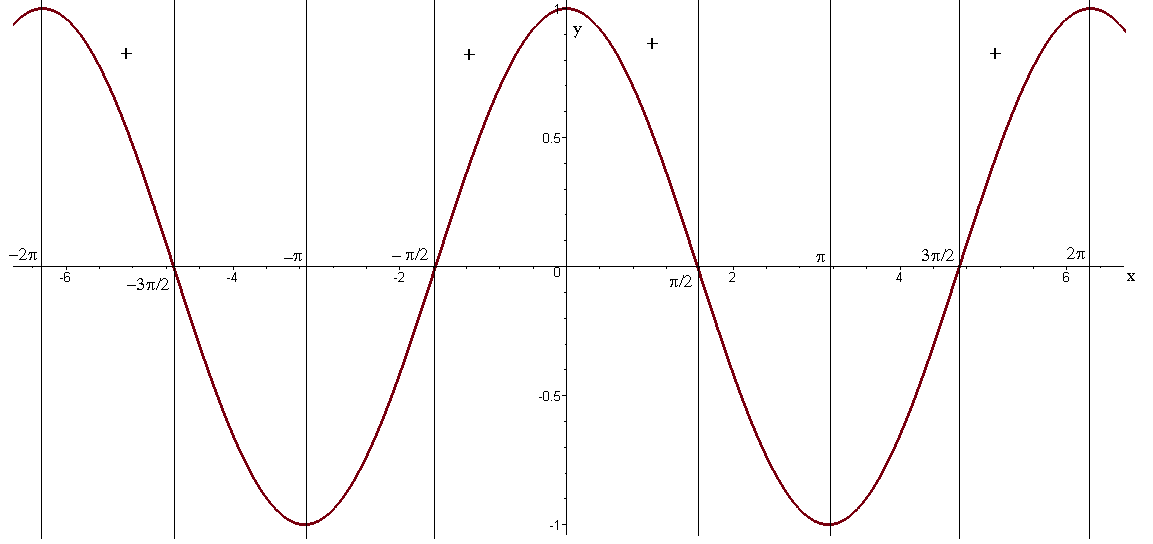
Рисунок 4 - График функции у = cos x
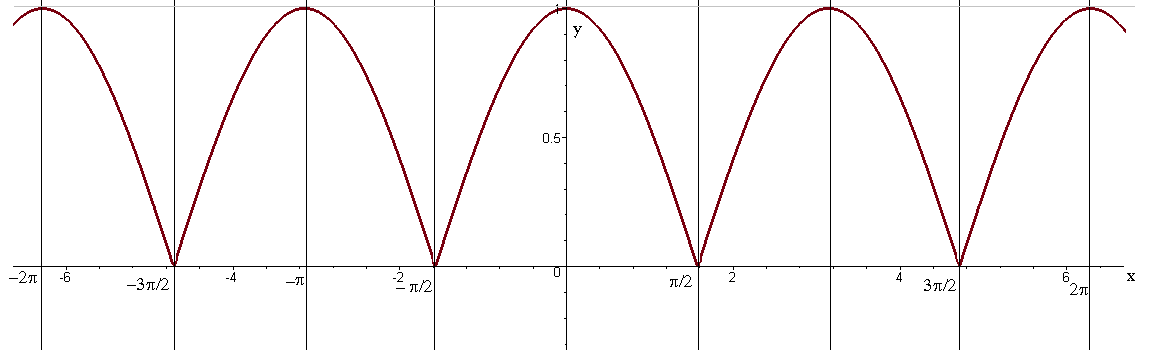
Рисунок 5 - График функции y=|cos x|
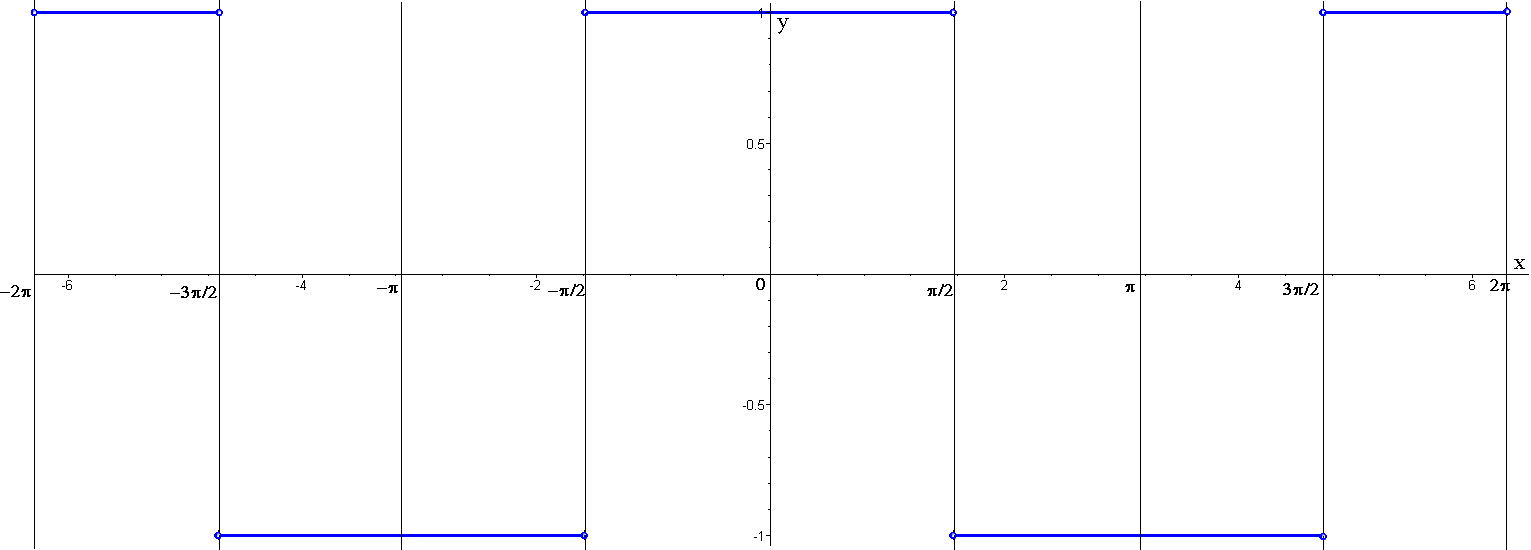
Рисунок 6 - График функции y=(cos x)/(|cos x|)
Теперь отобразим графически произведение двух функций и
; функцию
.
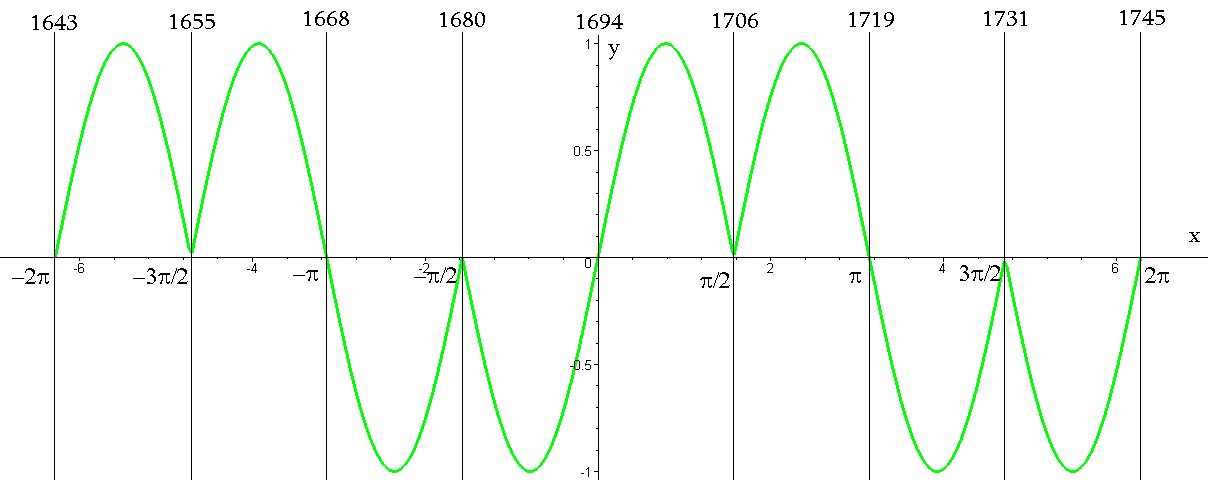
Рисунок 7 - Произведение двух функций y=sin 2x и y=cos x/|cos x|
В XVII веке в 1643-1649 годах казахская нация начала развиваться в субъективной форме, но в период 1649-1655 годов из-за конфликта ханов и султанов трех джузов она разрушилась и распалась в субъективной форме.
В 1655-1668 годах распавшиеся роды в какой-то степени развивались сами по себе, но в то же время они начинали разлагаться под влиянием внешнего воздействия джунгар.
В течение 1668-1680г.г. на фоне внешних политических факторов казахи объединились и развивались в объективной форме.
В период 1680-1694 (1681-1684) влияние привело к разъединению и убыванию. В результате осознания казахским народом угроз своему существованию, произошел подъем до стадий перехода от объективной формы к субъективной форме (примерно до 1700-х гг.).
До 1745 г. подобная динамика периодично повторялась. В 1731 году 10-го октября состоялся объединенный казахский курултай, где отказались от предложения России. По субъективным параметрам ограничено сверху, а по объективным параметрам ограниченность снизу, что выразилось в равномерной метрике (-1, 1).
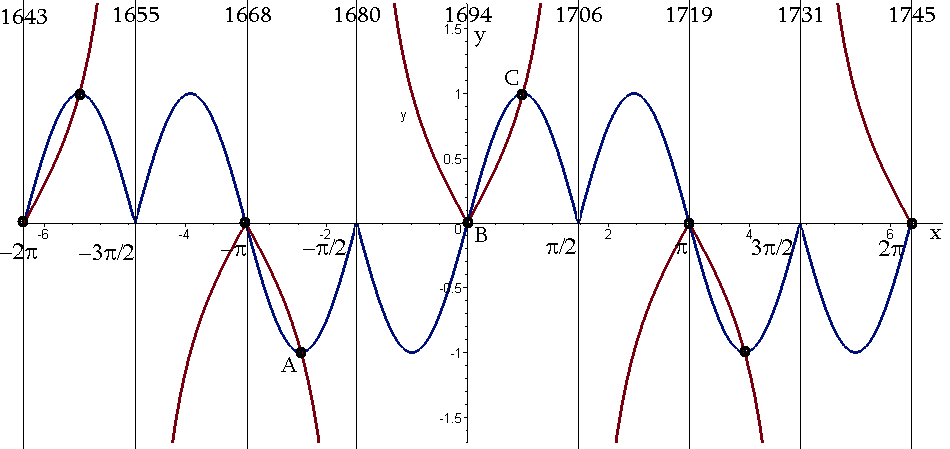
Рисунок 8 - Cопоставление историко-математических графиков
Точка А есть локальная окрестность 1674 года, в ней описывается напряжение между двумя странами в периоды упадка в объективной форме.
Точка В указывает на то, что в районе 1694 года психологическая ситуация казахской страны находилась на стадии бурного развития, а джунгарская страна находилась в состоянии упадка в своей субъективной форме и на стадии, когда она перешла на стадию развития.
Точка С – описывает 1699-1700гг., где произошла стычка Таукехана с Цэбдан Рабдоном.
На основе приведенного ранее алгоритма, выводов, результатов сопоставления исторических и математических графиков составим тригонометрическое уравнение:
Аналитическим способом решаем:
1) Область значений х: сos x≠0
2) а) при :
I.
II.
б) при
III.
IV.
Из 4-х случаев выберем точный ответ:
Заметим, что аналитическое решение однозначно совпадают с соответствующими точками при графическом решении.
Имеет место следующая теорема (критерий): для того чтобы описать политические и военные кризисы антагонистических противоречивости двух государств (Джунгар и Казахов) необходимо и достаточно сопоставить описывающие характеристических функции, которые имеют решения в некоторых частных случаях.
4. Заключение
Появление актуальных исследований о возможности применения современной математики для широкого круга самых разных наук и областей оказало большое влияние на школьную математику. Использование математических законов и теорем в исследованиях в области естественных наук давно и широко используется. В то же время мы все больше убеждаемся в наличии математических законов в области гуманитарных наук. В частности, подобными проблемами занимался академик В.И.Арнольд.
В данной научной работе представлен математический метод, направленный на выделение динамической картины джунгарского нашествия в период 1643-1745 гг. Данное исследование является одним из частных случаев применения тригонометрических объектов. Описание закономерностей такого рода, несомненно, вызывает интерес всех учащихся.