КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ ПНЕВМОЦИЛИНДРА ДВУСТОРОННЕГО ДЕЙСТВИЯ

Алексеев Д.П.¹, Кубенин А.С.² , Савельев А.А.³

¹ Старший преподаватель, Московский государственный индустриальный университет

² Ассистент, Московский государственный индустриальный университет

³ Студент, Московский государственный индустриальный университет

КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ ПНЕВМОЦИЛИНДРА ДВУСТОРОННЕГО ДЕЙСТВИЯ

Аннотация

В работе проводится исследование газодинамических процессов в пневмоцилиндре двустороннего действия на основе методов вычислительной гидродинамики. Для описания движения газа используются трехмерные уравнения Навье-Стокса, осредненные по Рейнольдсу. Изучается развитие во времени ударно-волновой структуры в поршневой полости пневмоцилиндра. С помощью компьютерного 3-D моделирования пневмоцилиндра двухстороннего действия в программном комплексе FlowVision проводится оценка правомерности использования квазистационарного одномерного приближения при решении задач расчета динамических характеристик пневмоцилиндра.

Ключевые слова: пневмоцилиндр, автоматизация, компьютерное моделирование.

Alekseev D.P. ¹, Kubenin A.S. ², Saveljev A.A. ³

¹Lecturer, Moscow State Industrial University

²Assistant, Moscow State Industrial University

³Student, Moscow State Industrial University

COMPUTER SIMULATION OF  DOUBLE-SIDED PNEUMOCYLINDER

Abstract

This paper deals with the study of gas-dynamic processes in the pneumatic cylinder double acting on the basis of methods of computational fluid dynamics. To describe the motion of the gas used three-dimensional Navier-Stokes equations, the Reynolds-averaged. We study the time evolution of the shock-wave structure in the air cylinder piston cavity. Using 3-D computer modeling double-acting pneumatic cylinder in the software package Aerohydrodynamic FlowVision analysis assesses the validity of the use of one-dimensional quasi-steady approach in solving problems of calculating the dynamic characteristics of the pneumatic cylinder.

Keywords: pneumocylinder, automating, computer simulation.

Введение.

Пневматические приводы  занимают ведущие позиции на предприятиях для автоматизации промышленных процессов и производственных циклов. Пневмосистемы распространены в автомобильной промышленности, в самолетостроении, в космонавтике, нефтяной, газовой и пищевой отрасли, где они применяются для автоматизации сборочных работ, для управления аварийными системами.

Каждый разработчик пневмодвигателей стремится увеличить быстродействие своих машин, так как это повышает их производительность. Также существенное значение имеет обеспечение износостойкости элементов пневмосистемы, особенно рабочего звена — пневмоцилиндра. Как известно, на износостойкость элементов большое влияние оказывают пульсации давления в их проточных областях. На производительность и износостойкость пневмоцилиндра могут оказывать влияние и ударные волны, способные формироваться в его полостях. Такие проблемы непосредственно связаны с разработкой методов динамического исследования машин и выбора их оптимальных параметров и структуры.   Одними из таких методов, безусловно, являются широко распространенные в наше время и динамично развивающиеся вычислительные методы на основе исторически сложившего моделирования поршня в одномерной постановке. К примеру, в работе [1].

В работе [2] автор излагает методы математического моделирования рабочих процессов в пневматических системах, предоставляет методики расчета основных параметров пневмоприводов, при которых обеспечивается максимальное быстродействие пневматических систем.

В работе [3] представлена математическая модель трехцилиндрового пневмодвигателя, которая позволяет вычислять динамические особенности движения поршня и газовые параметры с помощью программного обеспечения MATLAB-SIMULINK. Предложенный автором подход позволяет вычислять широкий набор термодинамических и эксплуатационных параметров для различных пневмоцилиндров.

Одномерные методики расчета не учитывают период установления течения в полостях пневмоцилиндра, когда течение в них имеет существенно нестационарный характер, в предельном случае с наличием ударных волн.

В данной работе на основе современного метода трехмерного компьютерного моделирования изучается ударно-волновая структура в поршневой полости цилиндра и ее взаимодействие с поршнем. Расчет проводится с допущением о мгновенной подаче сжатого воздуха в пневмоцилиндр, что соответствует идеальному случаю срабатывания дроссельной заслонки на входе в подводящий патрубок цилиндра.

Целью работы является исследование влияния ударно-волновой структуры течения, наблюдающейся в поршневой полости с момента подачи сжатого воздуха и до момента установления стационарной картины течения в данной полости, на динамические характеристики пневмоцилиндра двустороннего действия и, как следствие, оценка правомерности использования квазистационарного одномерного приближения для получения динамических характеристик пневмоцилиндра.

Компьютерное моделирование в программном комплексе FlowVision.

Перед созданием математической модели были приняты следующие допущения:

1) Рабочее тело - сжимаемый вязкий воздух.

2) Рассматривается 3D (трехмерная) постановка.

3)Режим течения — турбулентный.

Учитывая приведенные допущения уравнение сохранения массы (уравнение неразрывности) запишется в виде

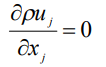Уравнения закона количества движения (Навье-Стокса) примут вид

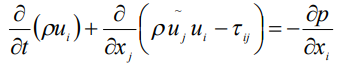где 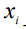- декартовы координаты (i=1,2); 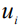- компоненты абсолютной скорости течения жидкости в направлении 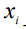; 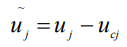- относительная скорость жидкости в локальной системе координат, двигающейся со скоростью 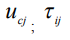- компоненты тензора напряжений

Для турбулентного течения выражение для тензора напряжений примет вид:

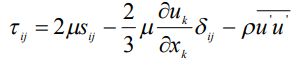где 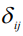 - символ Кронекера,  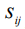- тензор скоростей деформации, определяемый как

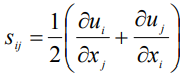Для определения турбулентной вязкости использовалась двухпараметрическая стандартная  \[k-\varepsilon \] модель.

Расчет рассмотренной математической модели проведен в сертифицированной программном комплексе аэрогидродинамического анализа FlowVision.

Для проведения моделирования был выбран пневмоцилиндр, параметры которого представлены в таблице 1.

Таблица 1

Диаметр поршня, D, мм	20
Рабочий ход поршня, L, мм	100
Длина поршня, мм	10
Масса поршня, m, кг	0,2

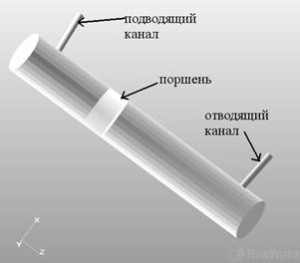
Созданная геометрическая модель пневмоцилиндра представлена

на рис.1.

Рис. 1 Геометрическая модель пневмоцилиндра

Размерность построенной сеточной модели составила 2 500 000 гексагональных ячеек.

В компьютерной модели пневмоцилиндра использовались следующие граничные условия:

• На стенках корпуса условие непротекания ,
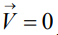• На входе в подводящий канал ,
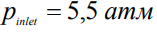• На выходе из отводящего канала .

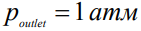В качестве начальных условий во всей расчетной области использовались следующие соотношения:.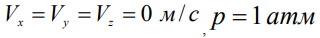

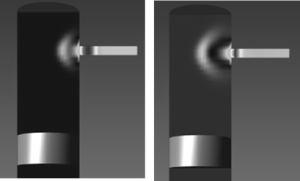
В начальный момент работы пневмоцилиндра в поршневой полости наблюдалась следующая ударно-волновая структура (рис. 2). Ударная волна поступает в поршневую полость пневмоцилиндра. После отражения от стенки постепенно рассеивается. С течением времени в поршневой полости давление выравнивается. Время установления давления в поршневой полости составляет порядка 1,5 мс. В течении этого периода времени поршень остается неподвижным.

Рис. 2 Ударно-волновая структура в поршневой полости пневмоцилиндра.

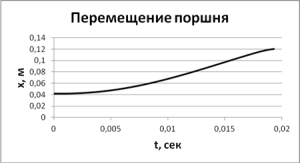
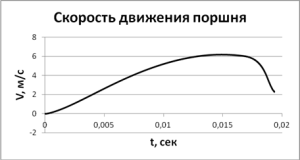
В результате расчета получены динамические характеристики пневмоцилиндра: зависимости перемещения и скорости движения поршня от времени приведены на рис. 3 и рис. 4, соответственно.

Рис. 3 Зависимость перемещение поршня от времени.

Рис. 4 Зависимость скорости движения поршня от времени.

 

Заключение.

Результаты компьютерного моделирования работы выбранного пневмоцилиндра в программном комплексе FlowVision позволяют провести оценку периода установления течения в полостях пневмоцилиндра. Показано, что движение поршня вследствие взаимодействия с ударной волной не происходит. Отсутствие влияния существенно нестационарной картины течения в поршневой полости цилиндра на движение поршня позволяет сделать вывод о том, что для моделирования данного пневмоцилиндра справедливо использовать концепцию квазистационарного подхода, используемую в одномерных методиках расчета пневмоцилиндра.

Литература

1. Герц Е.В. Расчет пневмоприводов / Е.В. Герц, Г.В. Крейнин. — М.: Машиностроение, 1975. —272 с.
2. Донской А. С. Математическое моделирование процессов в пневматических приводах: Учеб. Пособие. – СПб.: Изд-во Политехн. ун-та, 2009. – 121 с.
3. Muzaffar A., Computer simulation of pneumatic engine operation, Vol. 1 Issue 5, July - 2012, ISSN: 2278-0181