ДИНАМИКА ДИАМАГНИТНОГО РОТОРА В МАГНИТНОМ ПОЛЕ

Урман Ю.М.¹, Лапин Н.И.²

¹Доктор физико-математических наук, профессор, Нижегородский государственный педагогический университет имени К.Минина

²Старший преподаватель, Нижегородский государственный педагогический университет имени К.Минина

ДИНАМИКА ДИАМАГНИТНОГО РОТОРА В МАГНИТНОМ ПОЛЕ

Аннотация

В статье рассмотрено – вычисление моментов, действующих на диамагнитный ротор в магнитном поле, находятся первая и вторая гармоника, что позволяет рассмотреть угловые движения ротора. Записываются осредненные уравнения движения, выявляется характер движения вектора кинетического момента и движения относительно вектора кинетического момента.

Ключевые слова: левитация, неприводимый тензор, силовая функция.

Urman Yu.M.¹, Lapin N.I.²

¹Doktor of Physical and Mathematical Sciences, Nizhny NovgorodState Pedagogical University K.Minina

²Tutor, Nizhny NovgorodState Pedagogical University K.Minina

DIAMAGNETIC ROTOR DYNAMICS IN A MAGNETIC FIELD

Abstract

In the article - the calculation of the moments acting on the diamagnetic rotor in a magnetic field, are the first and the second harmonic, which allows to consider the angular movement of the rotor. Averaged equations of motion are written, revealed the nature of the vector of the angular momentum and the motion with respect to the angular momentum vector.

Keywords: levitation, irreducible tensor, force function.

В работе [1] показано, что потенциальную энергию произвольного по форме и размеру диамагнитного тела в неоднородном магнитном поле можно представить в виде

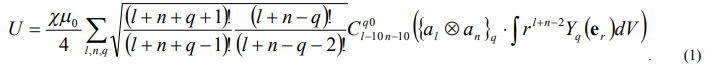
Здесь 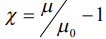- магнитная восприимчивость, 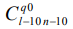- коэффициенты Глебша – Гордана [2]. На основании правила треугольника для коэффициентов Глебша – Гордана, индекс 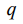принимает значения 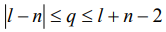. Кроме того накладывается условие на сумму трех индексов 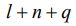, которая может быть только четной. Величины 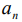- есть коэффициенты разложения потенциала внешнего магнитного поля на магнитные мультиполи в окрестности начала опорной системы координат в ряд по шаровым функциям 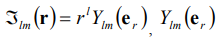- сферическая функция (функция, зависящая от направления единичного вектора 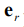), определенная без множителя 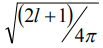[2]. Выражение в круглых скобках – скалярное произведение двух неприводимых тензоров, определяемых по правилу 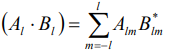[2]. При этом в формуле (1) тензорное произведение 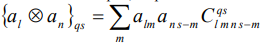связано с полем, а тензор 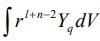- с телом ротора.

Для нахождения поля достаточно ограничиться первыми неисчезающими членами. Это связано с тем, что при разложении магнитного поля на мультиполи получается ряд, который сходиться на конечном расстоянии. Так, система токов, состоящая из двух витков с противонаправленными токами, будет определяться магнитным квадрупольным моментом, то есть второй гармоникой разложения потенциала. Поэтому рассмотрим только случай, когда магнитное поле состоит из однородной и градиентной составляющих.

Приведем несколько примеров:

1) Если в формуле (1) 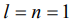, то

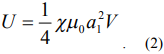
Из (2) следует, что взаимодействие однородного поля с диамагнитным телом произвольной формы не зависит от поворотов тела.

2) В формуле (1) 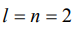(градиентное поле), тогда

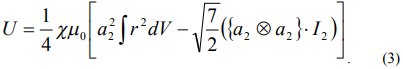
В выражении (3) 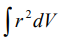- неприводимый тензор ранга 0, а 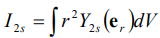- момент инерции тела единичной плотности – неприводимый тензор второго ранга. Если тело по форме эллипсоид, то вычисления представленных тензоров

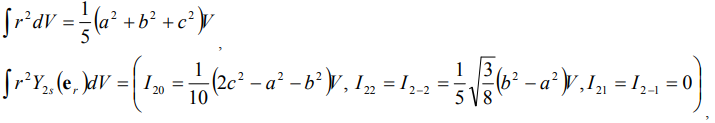
где a,b,c- главные полуоси эллипсоида, а 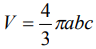- объем эллипсоида. Момент силы, действующий на диамагнитное тело в градиентном поле, определяется выражением

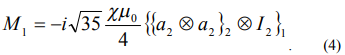
3) В формуле (1) 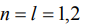, тогда

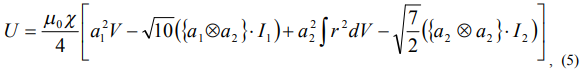
следовательно, момент сил, действующий на диамагнитный ротор, в поле, состоящем из однородной и градиентной составляющих, определяется формулой

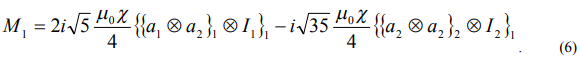
Аналогично можно рассмотреть влияние на диамагнитное тело полей более сложной конфигурации.

В формуле (5) величина 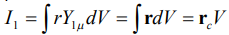- есть вектор центра масс однородного по плотности тела. Поэтому, если в качестве начала системы координат выбран центр масс, то влияние момент сил от однородной составляющей поля равно нулю.

Рассмотрим подвес, образованный двумя круговыми токами, направленными навстречу друг другу. Первый неисчезающий член разложения потенциала на оси относительно точки, в которой центр подвеса совпадает с центром масс тела, имеет вид

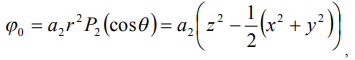
если сила тяжести действует вдоль оси подвеса, то тело сместиться и разложение потенциала на оси относительно центра подвеса будет иметь вид

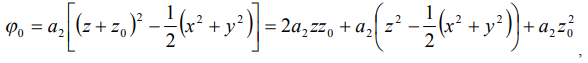
здесь 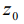- сдвиг центра масс диамагнитного тела вдоль направления силы тяжести относительно центра подвеса.

Таким образом, в новой системе координат, связанной с центром масс ротора, появится однородная составляющая поля вдоль оси системы

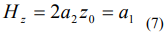
и, следовательно, появится сила 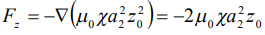, которая находится дифференцированием формулы (5) после подстановки в нее выражения (7).

В состоянии равновесия 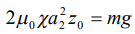, откуда 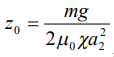, то есть смещение тела зависит от величины магнитного квадруполя.

Рассмотрим теперь угловые движения диамагнитного тела. Для этого введем следующие системы координат: 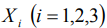- опорная, связанная с подвесом, 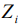- связанная с твердым телом. Вращение тела относительно неподвижной точки можно рассматривать как наложение двух движений: движение относительно кинетического момента и вместе с кинетическим моментом. Поэтому введем еще одну систему координат 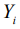, которая связана с вектором кинетического момента тела К. Ось 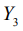сонаправлена с вектором К, оси системы 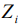направлены вдоль главных центральных осей эллипсоида инерции тела с моментами инерции соответственно 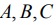. Переход от системы координат 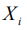к 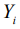осуществляется путем двух последовательных поворотов на сферические углы 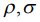, характеризующие положение вектора кинетического момента в системе 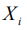, а от 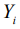к 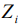после трех последовательных поворотов на углы Эйлера .

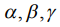В качестве переменных, задающих движение тела относительно неподвижной точки, выберем: величину 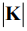кинетического момента, углы .

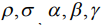Моменты (4) и (6) малы в силу малости величины магнитной проницаемости и для анализа движения тела можно применить аппарат асимптотических методов теории колебаний [3], который позволяет переменные, описывающие движение, разделить на быстрые и медленные. Обычно основное значение для анализа возмущенного вращения тела имеет характер изменения медленных переменных, эволюция которых описывается системой дифференциальных уравнений, более простой по сравнению с исходной системой.

Различный вид эволюционных уравнений рассмотрен в [4]. Мы возьмем вторую форму, где под 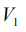будем понимать усредненную по быстрым переменным силовую функцию (3).

Чтобы провести осреднение, преобразуем силовую функцию к фазовым переменным задачи. Получаем

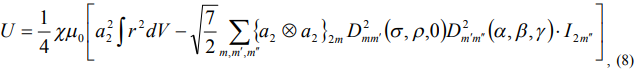
где 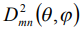- матрица конечных вращений [2].

Для осесимметричного поля ось 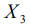опорной системы координат совпадает с осью поля, поэтому индекс m=0. Следовательно, силовая функция не зависит от угла 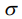. Осреднение силовой функции сводится к осреднению по свободному движению, которое представляет собой движение Эйлера – Пуансо. В работе [4] показано, что в нерезонансном случае, когда частоты свободного движения несоизмеримы, осреднение можно проводить двумя независимыми этапами: сначала по 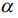, а затем по полодии.

Не нарушая общности, будем считать, что A<B<C. Осредняя по углу 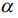получим, полагая в формуле (7) m'=0

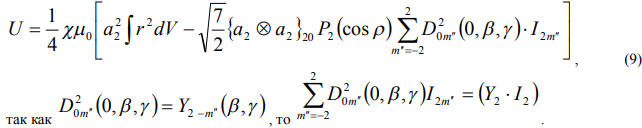
Осреднение по полодии сводится к вычислению интегралов вида [5] 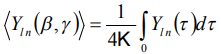, где K - полный эллиптический интеграл первого рода.

Осредненная силовая функция с точностью до константы будет иметь вид

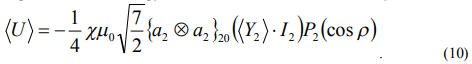
Уравнения эволюционных движений

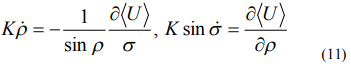
дают следующую картину движения диамагнитного тела в осесимметричном подвесе. Вектор кинетического момента, не меняя углового положения относительно оси поля 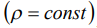, прецессирует вокруг оси с постоянной угловой скоростью прецессии

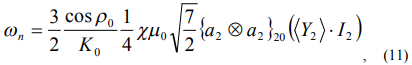
а вокруг вектора кинетического момента тело совершает свободные движения Эйлера – Пуансо.

Если тело обладает осью симметрии 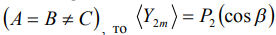. Картина движения не меняется, меняется только скорость прецессии.

Работа выполнена при финансовой поддержке РФФИ грант № 12-01-31133