АЛГОРИТМ МОДЕЛИРОВАНИЯ НАГРУЗОК НА ЭЛЕМЕНТЫ ЛЕСНЫХ МАШИН В ВИДЕ ГАУССОВСКИХ СЛУЧАЙНЫХ ПРОЦЕССОВ

DOI:https://doi.org/10.23670/IRJ.2022.119.5.046

АЛГОРИТМ МОДЕЛИРОВАНИЯ НАГРУЗОК НА ЭЛЕМЕНТЫ ЛЕСНЫХ МАШИН В ВИДЕ ГАУССОВСКИХ СЛУЧАЙНЫХ ПРОЦЕССОВ

Научная статья

Будевич Е.А.¹, Тимохова О.М.², Вычерова Н.Р.^3, *

¹ ORCID: 0000-0003-1072-7687;

²ORCID: 0000-0003-3179-6382;

³ ORCID: 0000-0001-9631-4300;

^{1, 2, 3} Ухтинский государственный технический университет,Ухта, Россия

^*Корреспондирующий автор (nvycherova[at]ugtu.net)

Аннотация

В статье проанализировано разнообразие технологических операций (таких как нагрузка на крутящий момент, нагрузка на ось автомобиля, нагрузка на детали трансмиссии и др.) и движения лесных машин, в ходе которого технологическое оборудование испытывает нагрузки, которые являются случайными функциями времени t, т. е. случайными процессами.

Результаты моделирования одного из распространённых видов нагрузок, т.е. крутящего момента (КМ), в тексте представленного стационарным гауссовским процессом , являются исходной информацией для прогнозирования усталостной долговечности деталей ЛМ на стадии проектирования без проведения натурных испытаний и осциллографирования случайных процессов нагрузок.

Представленный алгоритм моделирования можно применить для моделирования нагруженности и прогноза ресурса элементов новой лесной техники.

Ключевые слова: гауссовские случайные процессы, алгоритм моделирования.

MODELING ALGORITHM OF LOADS ON FOREST MACHINES ELEMENTS IN FORM OF GAUSSIAN RANDOM PROCESSES

Research article

Budevich E. A.¹, Timohova O. M.², Vycherova N. R.^{3, *}

¹ORCID: 0000-0003-1072-7687;

²ORCID: 0000-0003-3179-6382;

³ORCID: 0000-0001-9631-4300;

^{1, 2, 3}Ukhta State Technical University, Ukhta, Russia

^*Corresponding author (nvycherova[at]ugtu.net)

Abstract

The article analyzes the variety of technological operations (such as load on torsion torque, load on vehicle axle, load on transmission parts, etc.) and the movement of forest machines, during which the technological equipment is under load, that are chance time t functions, t.e. chance processes.

Results of one of the common load types modeling, i.e.torsion torque (TT), are presented by the stationary Gaussian process, and are the basic information for prediction of fatigue design life of FM parts at the design stage without full-scale tests and oscillation of random load processes.

The presented modeling algorithm can be used to simulate the load and predict the resource of elements of new forest technology.

Keywords: Gaussian random processes, chance processes, modeling algorithm.

Введение

Из–за разнообразия технологических операций и движения лесных машин (ЛМ) по дорогам и волокам случайного профиля, многие детали трансмиссии, ходовой системы и технологического оборудования испытывают нагрузки, которые являются случайными функциями времени t, т. е. случайными процессами. Одним из распространенных видов нагрузок является крутящий момент (КМ), который представим стационарным гауссовским процессом , обладающим свойством эргодичности (специальное свойство некоторых динамических систем, состоящее в том, что в процессе эволюции почти каждое состояние с определённой вероятностью проходит вблизи любого другого состояния системы). При этом условии достаточно рассмотреть не множество реализаций ансамбля, а одну реализацию КМ достаточной продолжительности. Вышеуказанные воздействия относят к категории случайных колебаний, опасность их состоит в том, что они приводят к повышенному росту усталостных трещин.

Существующие методы статистического анализа нагруженности основаны на записи осциллограмм. Такой путь требует больших затрат времени и средств на проведение натурных тензометрических испытаний, и информация получается с большим опозданием.

Для преодоления этих трудностей предложен алгоритм статистического моделирования случайных процессов нагружения деталей ЛМ, реализация которого возможна только на ПЭВМ [1, С. 72].

Методы и принципы исследования

Алгоритм моделирования  состоит в следующем. Задаемся приближенно возможными границами КМ: нижней – МH и верхней – MB. С помощью математической функции RND(x) (язык программирования QBasic) генерируем последовательность случайных чисел {ri}n двойной точности, равномерно распределенных в открытом интервале от 0 до 1. По этим значениям моделируем равномерное распределение КМ по соотношению:

 

Затем строим случайную выборочную функцию – Mt. Для этого значения М1, М2, …., Мn, полученные по (5), откладываем на n последовательных ординатах, расположенных через равные интервалы t =  (шаг квантования) по оси времени t. Ординаты реализаций 1 M t , 2 M t , …, n M t , в эти моменты времени можно рассматривать кактреальную осциллограмму записи КМ [5, C. 207]. По этим значениям вычисляем выборочную коррелирующую функцию (КФ) для КМ по формуле:

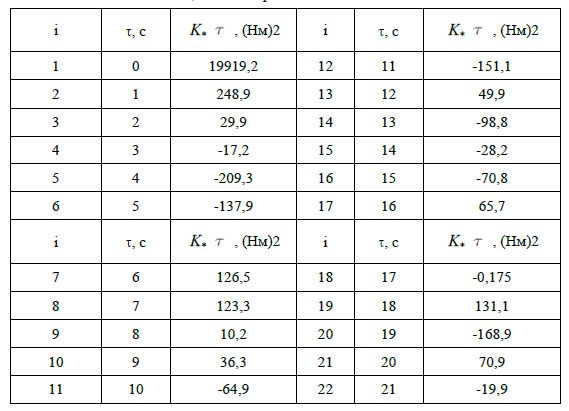
Приведем результаты моделирования КМ в виде стационарного гауссовского процесса  [8, С. 136], для карданного вала трактора ЛТ-154 при движении на III-й передаче. Для этого составлена программа (язык Qbasic). Нижняя и верхняя границы для КМ соответственно равны: МН=250 Нм, МВ=740 Нм. При этих данных по (1) смоделирована выборка объемом n=4000 значений и по (2) – (3) вычислены характеристики:  Нм, S=141,4. Затем по (4) смоделируем последовательность {ri}n, а по (5) выборочное распределение КМ по нормальному закону [9, С. 76]. Частичные реализации КМ, полученные по (5), представлены в таблице 1. На основании смоделированных данных, по (6) определяем выборочные значения КФ – K*(τ), которые представлены в таблице 2, при шаге квантования Dt=t =1 c, при этом полученные значения: τ1=2,6 с, τ2=4 с и τ3=5,5 с, по которым по (8) вычислены параметры аппроксимации (7): a=3,9 c-1, b=1,1 c-1.

Таблица 1 – Частичные реализации КМ

t, c	Mi, Hм	t, c	Mi, Hм	t, c	Mi, Hм	t, c	Mi, Hм
1	2	3	4	5	6	7	8
0	0,0	21	642,7	42	217,9	63	484,9
1	501,9	22	462,7	43	464,2	64	788,4
2	525,3	23	219,4	44	500,0	65	553,6
3	600,2	24	578,4	45	499,8	66	659,3
4	610,6	25	495,8	46	754,1	67	731,7
5	563,6	26	503,5	47	427,1	68	538,6
6	502,5	27	430,6	48	478,7	69	444,9
7	655,4	28	384,7	49	545,1	70	608,8
8	439,5	29	667,3	50	425,1	71	544,3
9	517,1	30	582,8	51	483,9	72	669,0
10	279,4	31	410,9	52	430,1	73	461,2
11	579,5	32	532,8	53	503,9	74	581,0
12	407,4	33	547,4	54	592,7	75	326,9
13	333,6	34	324,9	55	434,6	76	658,4
14	339,4	35	346,0	56	713,6	77	842,3
15	448,9	36	528,2	57	531,3	78	444,9
16	415,0	37	780,3	58	392,8	79	699,4
17	660,4	38	394,5	59	153,3	80	544,8
18	449,2	39	600,0	60	478,6	81	184,2
19	727,9	40	411,8	61	673,3	82	526,1
20	427,6	41	554,5	62	549,6	83	642,2

Таблица 2 – Выборочные значения

Выводы

Результаты моделирования  являются исходной информацией для прогнозирования усталостной долговечности деталей ЛМ на стадии проектирования без проведения натурных испытаний и осциллографирования случайных процессов нагрузок. Аналогичным образом моделируются и другие виды случайного нагружения деталей ЛМ: растяжение-сжатие, изгиб, изгиб с кручением. При ряде допущений алгоритм позволяет моделировать случайные процессы, когда амплитуды нагрузок подчинены анормальным распределениям. В этом случае меняются отдельные блоки программы.

Алгоритм можно применить для моделирования нагруженности и прогноза ресурса элементов новой лесной техники.

Конфликт интересов Не указан.

Conflict of Interest None declared.

Списоклитературы / References

1. Ермаков С. М. Статистическое моделирование / С. М. Ермаков, Г. А. Михайлов. – 2-е изд., доп. – М.: Наука, Главная редакция физико-математической литературы, 1982. – 296 с.
2. Свешников А.А. Прикладные методы теории случайных функций / А. А. Свешников – 2-е изд., перераб. и доп. – М.: Наука, Главная редакция физико-математической литературы, 1968. – 464 с.
3. Михайлов Г. А. Некоторые вопросы теории методов Монте-Карло / Г. А. Михайлов. – Новосибирск: Наука, 1974.– 304 с.
4. Ермаков С. М. Метод Монте-Карло и смежные вопросы / С. М. Ермаков – 2-е изд., доп. – М.: Наука, Главная редакция физико-математической литературы, 1975. – 473 с.
5. Александров В. А. Моделирование технологических процессов лесных машин / В. А. Александров, А. В. Александров. – 3-е изд., перераб. – СПб.: Лань, 2016. – 368 с.
6. Светлицкий В. А. Статистическая механика и теория надёжности / В. А. Светлицкий. – М.: Изд-во МГТУ им. Н. Э. Баумана, 2002. – 504 с.
7. Любимов И. И. Динамика колесной нагрузки при колебаниях автомобиля / И. И. Любимов // Вестник Саратовского государственного технического университета. – 2004. – № 4 (5). – С. 33-38.
8. Гусев А. С. Расчёт конструкций при случайном воздействии / А. С. Гусев, В. А. Светлицкий. – М.: Машиностроение, 1984. – 204 с.
9. Александров В. А. Динамические нагрузки в лесосечных машинах / В. А. Александров. – Л.: ЛГУ, 1984. – 152 с.
10. Брауде В. И. Вероятностные методы расчёта грузоподъёмности машин / В. И. Брауде. – Л.: ЛГУ, 1978. – 230 с.
11. Ветцель Е. С. Теория случайных процессов и её инженерные приложения / Е. С. Ветцель, Л. А. Овчаров. – М.: Высш. шк., 2000. – С. 331-350.

Список литературы на английском языке / References in English

1. Ermakov S. M. Statisticheskoe modelirovanie [Statistical modeling] / S. M. Ermakov, G. A. Mihajlov - 2nd edition, enlarged. – M.: Nauka, Main editorial of physics and mathematics literature, 1982. – 296 p. [in Russian]
2. Sveshnikov A.A. Prikladnye metody teorii sluchajnyh funkcij [Applica-tional methods of arbitrary function theory] / A. A. Sveshnikov. – 2nd edition, re-visited and enlarged. – M.: Main editorial of physics and mathematics literature, 1968. – 464 p.[in Russian]
3. Mihajlov G. A. Nekotorye voprosy teorii metodov Monte-Karlo [Some questions on the Monte Carlo method theory] / G. A. Mihajlov. – Novosibirsk: Nauka publishing house, 1974. – 304 p. [in Russian]
4. Ermakov S.M. Metod Monte-Karlo i smezhnye voprosy [Monte Carlo method and related questions] / S.M. Ermakov. – 2nd edition revised. – M.: Nauka Main editorial of physics and mathematics literature, 1975. – 473 p. [in Russian]
5. Aleksandrov V. A. Modelirovanie tekhnologicheskih processov lesnyh mashin [Modeling of technological processes of forest machines] / V. A. Aleksan-drov, A. V. Aleksandrov. – 3rd edition, revised. – SPB.: Lan' publishing house, 2016. – 368 p. [in Russian]
6. Svetlickij V. A. Statisticheskaya mekhanika i teoriya nadyozhnosti [Statis-tical mechanics andreliability theory]/V. A. Svetlickij. – M.: Bauman MSTUPublishing house, 2002. – 504 p. [in Russian]
7. Lyubimov I. I. Dinamika kolesnoj nagruzki pri kolebaniyah avtomobilya [Dynamics of the wheel load in case of automobile fluctuations] / I. I. Lyubimov // Vestnik Saratovskogo gosudarstvennogo tekhnicheskogo universiteta [Bulletin of SSTU]. – 2004. – № 4 (5). – P. 33-38. [in Russian]
8. Gusev A. S. Raschyot konstrukcij pri sluchajnom vozdejstvii [ Calculation of structures at random impact] / A. S. Gusev, V, A. Svetlickij. – M.: Mashi-nostroenie publishing house, 1984. – 204 p.[in Russian]
9. Aleksandrov V. A. Dinamicheskie nagruzki v lesosechnyh mashinah [Dynamic loads in forestry machines] / V. A. Aleksandrov. – L.: LGU 1984. – 152 p. [in Russian]
10. Braude V. I. Veroyatnostnye metody raschyota gruzopod"yomnosti mashin [Probabilistic methods of calculating the load capacity of machines] / V. I. Braude. – L.: LGU 1978. – 230 p. [in Russian]
11. Vetcel E. S. Teoriya sluchajnyh processov i eyo inzhenernye prilozheni-ya [theory of random processes and its supplemets] / E. S. Vetcel, L. A. Ovcharov. – М.: Higher school publishing house, 2000.P. 331-350. [in Russian]