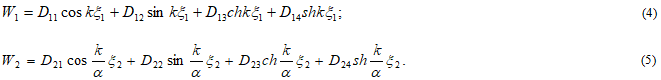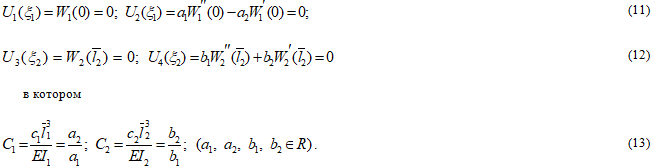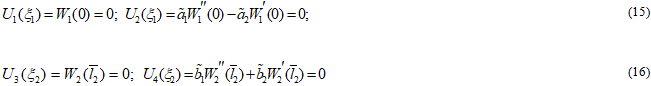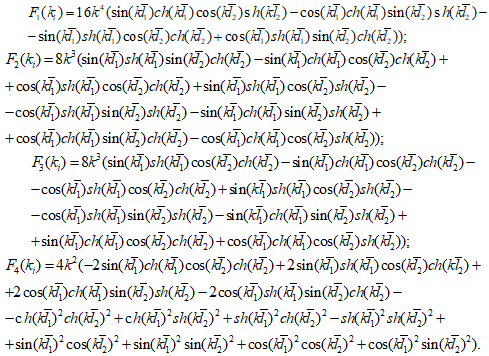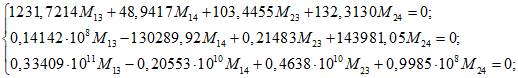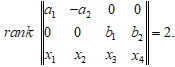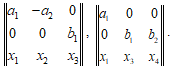ВОССТАНОВЛЕНИЕ ЖЕСТКОСТНЫХ ПАРАМЕТРОВ ДВУХСЕГМЕНТНОЙ БАЛКИ С УЧЕТОМ АБСОЛЮТНО ЖЕСТКИХ ЗАКРЕПЛЕНИЙ

ВОССТАНОВЛЕНИЕ ЖЕСТКОСТНЫХ ПАРАМЕТРОВ ДВУХСЕГМЕНТНОЙ БАЛКИ С УЧЕТОМ АБСОЛЮТНО ЖЕСТКИХ ЗАКРЕПЛЕНИЙ

Научная статья

Сафина Г.Ф.*

ORCID: 0000-0002-7326-0896,

Нефтекамский филиал Башкирского государственного университета, Нефтекамск, Россия

* Корреспондирующий автор (safinagf[at]mail.ru)

Аннотация

Рассмотрена обратная задача диагностирования жесткостных параметров изгибных колебаний двухсегментной балки по известным значениям частот ее колебаний. Показана единственность решения обратной задачи, сформулирована и доказана соответствующая теорема. Найден алгоритм решения задачи, подтверждающий единственность восстановления жесткостных параметров опор балки, который применим и для случая абсолютно жестких закреплений краев двухсегментной балки. Алгоритм решения подтвержден численными примерами.

Ключевые слова: двухсегментная балка, частоты колебаний, обратная спектральная задача, диагностирование параметров.

RESTORATION OF THE STIFFNESS PARAMETERS OF A TWO-SEGMENT BEAM, TAKING INTO ACCOUNT RIGID ATTACHMENT

Research article

Safina G.F.*

ORCID: 0000-0002-7326-0896,

Neftekamsk Branch of Bashkir State University, Neftekamsk, Russia

* Corresponding author (safinagf[at]mail.ru)

Abstract

The current study examines the inverse problem of diagnosing the stiffness parameters of flexural vibrations of a two-segment beam from known values of its vibration frequencies. The author of the study shows the uniqueness of the solution of the inverse problem as well as formulates and proves the corresponding theorem. The article introduces an algorithm for solving the problem that confirms the uniqueness of restoring the stiffness parameters of beam bearings, which is also applicable for the case of rigid attachment of the edges of a two-segment beam. The solution algorithm is confirmed by numerical examples.

Keywords: two-segment beam, oscillation frequencies, inverse spectral problem, parameter diagnostics.

Исследуя вибрационные процессы механических систем, технических конструкций и их составляющих часто можно столкнуться с поперечными колебаниями балок. Прямые и обратные спектральные задачи по балкам хорошо известны еще из общей теории колебаний, например, [1], [3]. Производимые расчеты исследований учитывают разные виды балок: однородные, неоднородные, деформированные, сегментные, с трещинами, несущие, под действием переменных сил, подвижных нагрузок и т.д.

Математические модели колебаний сегментных балок встречаются также во многих работах, например [4], [5]. В монографии [5] приведены численные примеры решения коэффициентных обратных задач балок (в том числе сегментных) на основе сочетания граничных интегральных уравнений и метода конечных элементов. Прямой и обратной задачам двухсегментной балки посвящены также статьи [6], [7]. В представленной же работе в продолжение исследований доказана единственность решения обратной задачи для двухсегментной балки и дан метод восстановления граничных условий технологиями линейной и векторной алгебры. Кроме того, приведенный метод учитывает возможность абсолютно жестких закреплений концов сегментной балки.

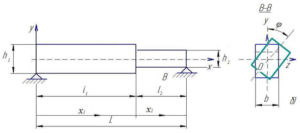
Для дальнейшего изложения остановимся кратко на решении прямой задачи и получении векового уравнения (с учетом как условий опор, так и условий сопряжения сегментов балки). Итак, динамическая модель двухсегментной балки представле­на на рисунке 1. Сегменты балки c длинами   имеют различные жёсткости , образующиеся за счет поворота на угол φ в месте сопряжения.

Рис. 1 – Модель двухсегментной балки

В соответствии с расчетной схемой уравнения изгибных колебаний такой балки имеют вид [1], [2], [3]:      (1)

В (1):  – прогиб i-го сегмента (x_i – локальные координаты, t – время),  ρ – погонная плотность материала балки,  – площадь поперечного сечения каждого сегмента ,  – момент инерции поперечного сечения балки, причем .

Введение безразмерных параметров:  приводит к уравнениям

    (2)

Представление прогибов сегментов балки в виде  – безразмерная собственная частота колебаний, приводит уравнения (2) к видам:

в которых  – волновое число.

Решения (3) для каждого сегмента приняты в стандартном виде с амплитудами колебаний :

В соответствие с (4) и (5) для каждого сегмента определены повороты поперечного сечения сегментов, изгибающие моменты и поперечные силы, необходимые для описаний условий сопряжения:

и граничных условий:

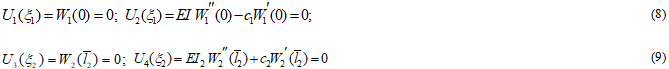
в виде шарнирных опор с пружинами кручения с жесткостями . Подстановка решений (4), (5) в условия сопряжения (6), (7) и в краевые условия (8), (9) дает восемь однородных алгебраических уравнений относительно констант интегрирования . С учетом нетривиального решения этой системы получено вековое уравнение прямой спектральной задачи [7]:

   (10)

с безразмерными параметрами  из сумм и произведений тригонометрических и гиперболических функций от аргументов .

С учетом математической модели (10) и программной реализации алгоритма решения в математическом пакете Maple найдены значения частот изгибных колебаний двухсегментной балки. Поставлена и решена также обратная задача определения жесткостных параметров закреплений по известным трем частотам колебаний.

Этот метод решения обратной задачи не принимает во внимание случай, когда края балки закреплены абсолютно жёстко, то есть, когда  В связи с этим рассмотрим другой подход к решению обратной задачи, который позволит восстановить и возможное абсолютно жесткое закрепление ее краев.

Для этого граничные условия задачи (3), (8), (9) представим в виде:

Составим матрицу A из коэффициентов форм  краевых условий (11), (12):

а также ненулевые миноры  второго порядка этой матрицы:

    (14)

Тогда обратную задачу восстановления жесткостей шарнирных опор двухсегментной балки смоделируем в виде нахождения матрицы A (по ее минорам), что можно свести к определению оболочки   на векторах .

Для исследования существования и единственности такого решения наряду с нашей прямой задачей (3), (11), (12) рассмотрим задачу с уравнениями (3) и граничными условиями

Оболочку на векторах  из коэффициентов (15), (16) рассмотрим в виде . Докажем теперь следующую теорему.

Теорема

Если выполняются условия:

   (17)

и нетривиальные собственные значения  задач (3), (11), (12) и (1), (15), (16), соответственно, равны учетом их кратностей, то равны и оболочки  и .

Доказательство

Вековое уравнение граничной задачи (3), (11) (12) найдем стандартными преобразованиями, подставляя решения (4), (5) в граничные условия (11), (12) и условия сопряжения сегментов (6), (7). Получим систему уравнений:

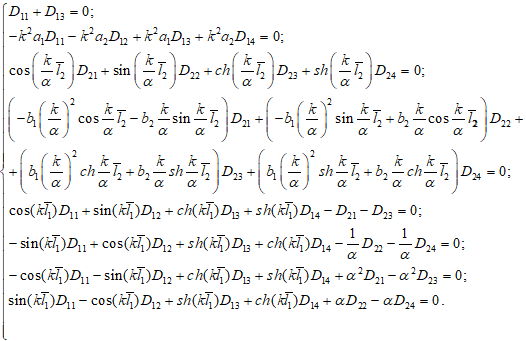В итоге вековое уравнение получим в виде определителя 8-го порядка:

Раскрывая определитель    с учетом миноров (14) матрицы A получим вековое уравнение в виде:

     (18)

в котором функции ,  примут вид:

    (19)

Заметим, что вековое уравнение задачи (3), (15) (16) будет иметь аналогичный (18) вид, а именно

      (20)

причем функции  также будут иметь выражения, аналогичные (19).

Полученные уравнения (18) и (20) являются целыми функциями порядка ½ [8], тогда имеем соотношения:

   (21)

где K – нетривиальная константа. Тогда, учитывая (13) и сами выражения вековых уравнений, можем записать равенство:

   (22)

Применяя далее команды математического пакета Maple, можно показать линейную независимость функций  (раскладывая их, например, в степенной ряд).

Далее учетом (22) и линейной независимости функций  имеем:

   (23)

откуда следует пропорциональность бивекторов . Из их пропорциональности следует соответствие подпространств оболочек.

Таким образом, оболочка  восстанавливается единственным образом. Теорема доказана.

Рассмотрим теперь алгоритм определения этого решения. Если известны собственные значения  задачи (3), (11), (12), то, подставляя их в вековое уравнение (18), получим систему трех уравнений от неизвестных  миноров матрицы A граничных условий.

Исходя из теоремы, данная система разрешается однозначно с точностью до ненулевого константа, т.е. определяет бивектор

С помощью найденных миноров определяется сама матрица A (с точностью до эквивалентных матриц), т.е. восстанавливаются граничные условия спектральной задачи, в том числе и случай абсолютно жестких закреплений концов двухсегментной балки.

Пример 1

Пусть  – собственные значения задачи (3), (11), (12), соответствующие первым трем собственным частотам изгибных колебаний двухсегментной балки с физическими и геометрическими параметрами

     (24)

Определим матрицу A с точностью до эквивалентных матриц, тем самым восстановим жесткостные параметры граничных условий балки.

Решение

При заданных собственных значениях  с помощью команд пакета Maple находим по формулам (19) соответствующие функции  и имеем систему уравнений (18) в виде:

В этом же пакете получаем решение системы:

Здесь С – некоторая нетривиальная константа.

Тогда бивектор  можно считать приближенно равным (с точностью до константы): . Найдем далее оболочку  данного бивектора. Для этого рассмотрим некоторый произвольный вектор  искомой оболочки, тогда координаты вектора  удовлетворяют условию

С учетом того, что есть ненулевые миноры, например, , можно из последнего равенства получить равенство нулю окаймляющих  миноров

Последние определители разложим, например, по третьей строке:

Тогда произвольный вектор искомой оболочки примет вид , а базисными векторами этой оболочки могут служить векторы .

В итоге матрицу  граничных условий имеем в виде: 

В соответствие с равенствами (13) имеем следующие безразмерные и размерные параметры жесткостей пружин кручения шарнирных опор двухсегментной балки:

Коэффициенты жесткостей опор балки восстановлены верно, поскольку при решении прямой задачи (3), (11), (12) именно значения жесткостей  (при остальных параметрах (24) балки) определяют заданные собственные значения .

Пример 2

Решить обратную спектральную задачу для двухсегментной балки с параметрами (24) при известных собственных значениях: .

Решение

Система уравнений (18) при заданных значениях  и физических параметрах имеет решение: 

где С – нетривиальная константа. Значит имеем бивектор  с точностью до константы в виде .

Аналогичные рассуждения и проведенные как в примере 1 преобразования, дают приближения:

Значит базисные векторы ,  и матрица A:

С учетом (13) и (24) получаем, что коэффициенты жесткостей опор балки стремятся к бесконечности, что говорит об абсолютно жестких закреплениях обоих краев двухсегментной балки.

Таким образом, представленный алгоритм решения обратной граничной задачи позволяет по трем частотам изгибных колебаний балки восстанавливать единственным образом ее жесткостные параметры ее шарнирных опор, в том числе и абсолютно жесткие закрепления.

Конфликт интересов Не указан.

Conflict of Interest None declared.

Список литературы / References

1. Ганиев Р.Ф. Колебания твердых тел / Р.Ф. Ганиев, В.О. Кононенко – М.: Наука, 1976. – 432 с.
2. Бабаков И.М. Теория колебаний / И.М. Бабаков. – М.: Дрофа, 2004. – 591с.
3. Горяченко В. Д. Элементы теории колебаний / В.Д. Горяченко – М.: Наука, 2001. – 395 с.
4. Доев В.С. Поперечные колебания балок / В.С. Доев – М.: КНОРУС, 2016. – 412 с.
5. Ватульян А.О. Прямые и обратные задачи для однородных и неоднородных упругих и электроупругих тел / А.О. Ватульян, А.Н. Соловьев – Ростов н/Д: ЮФУ, 2008. – 176 с.
6. Сафина Г.Ф. Исследования поперечных колебаний шарнирно-опертой балки ступенчато-переменного сечения / Г.Ф. Сафина, К.И. Хусаинова // Физическое образование в вузах. – 2018. – Т.24. №1S. – С.111-113.
7. Сафина Г.Ф. Моделирование в прямой и обратной задачах колебаний балки из двух сегментов / Г.Ф. Сафина // Современные наукоемкие технологии. – 2019. – №5. – С. 75-80.
8. Иванов В.К. Теория линейных некорректных задач и ее приложения / В. К. Иванов, В. В. Васин, В.П. Танана. – М.: Наука, 1978. – 200 с.

Список литературы на английском языке / References in English

1. Ganiev R.F. Kolebanija tverdyh tel [Solid vibrations] / R.F. Ganiev, V.O. Kononenko – M.: Nauka, 1976. – 432 p. [in Russian]
2. Babakov I.M. Teorija kolebanij [Wave theory] / I.M. Babakov. – M.: Drofa, 2004. – 591 p. [in Russian]
3. Gorjachenko V. D. Jelementy teorii kolebanij [Elements of vibration theory] / V.D. Gorjachenko – M.: Nauka, 2001. – 395 p. [in Russian]
4. Doev V.S. Poperechnye kolebanija balok [Transverse vibrations of beams] / V.S. Doev – M.: KNORUS, 2016. – 412 p. [in Russian]
5. Vatul'jan A.O. Prjamye i obratnye zadachi dlja odnorodnyh i neodnorodnyh uprugih i jelektrouprugih tel [Direct and inverse tasks for homogeneous and inhomogeneous elastic and electrically elastic bodies] / A.O. Vatul'jan, A.N. Solov'ev – Rostov n/D: JuFU, 2008. – 176 p. [in Russian]
6. Safina G.F. Issledovanija poperechnyh kolebanij sharnirno-opertoj balki stupenchato-peremennogo sechenija [Studies of transverse vibrations of the hinged-supported beam of stepwise-variable section] / G.F. Safina, K.I. Husainova // Fizicheskoe obrazovanie v vuzah. [Physical education in universities] – 2018. – Vol.24. №1S. – P. 111-113. [in Russian]
7. Safina G.F. Modelirovanie v prjamoj i obratnoj zadachah kolebanij balki iz dvuh segmentov [Simulation in direct and reverse problems of beam oscillations from two segments] / G.F. Safina // Sovremennye naukoemkie tehnologii. [Modern knowledge-intensive technologies] – 2019. – №5. – P. 75-80. [in Russian]
8. Ivanov V.K. Teorija linejnyh nekorrektnyh zadach i ee prilozhenija [The theory of linear incorrect problems and its applications] / V. K. Ivanov, V. V. Vasin, V.P. Tanana. – M.: Nauka, 1978. – 200 p. [in Russian]