ПРИНЦИПЫ МОДЕЛИРОВАНИЯ ПРИ ПРОЕКТИРОВАНИИ АВТОМОБИЛЬНЫХ ДОРОГ НА ОСНОВЕ ЛИНЕЙЧАТОЙ ГЕОМЕТРИИ

ПРИНЦИПЫ МОДЕЛИРОВАНИЯ ПРИ ПРОЕКТИРОВАНИИ АВТОМОБИЛЬНЫХ ДОРОГ НА ОСНОВЕ ЛИНЕЙЧАТОЙ ГЕОМЕТРИИ

Научная статья

Шангина Е.И.*

ORCID: 0000-0001-5433-8400;

Уральский государственный горный университет, Екатеринбург, Россия

* Корреспондирующий автор (eishangina[at]yandex.ru)

Аннотация

Традиционно при проектировании откосов железнодорожных путей и автомобильных дорог используют специальные поверхности. Такие поверхности должны удовлетворять определённым инженерным и технологическим требованиям. С геометрической точки зрения эти поверхности, чаще всего, представляют собой линейчатые и цилиндрические поверхности. В статье представлен обзор поверхностей Каталана, их применение в архитектуре, показаны примеры в природе, а также разработан алгоритм конструирования линейчатых поверхностей, в частности, поверхности равнодлинного откоса и поверхности одинакового ската. Прикладное значение этих поверхностей то, что эти поверхности могут являться геометрическими моделями откосов дорог.

Ключевые слова: геометрическое моделирование, откосы дорог, линейчатые поверхности, поверхности Каталана.

PRINCIPLES OF MODELING IN DESIGNING LINEAR GEOMETRY-BASED HIGHWAYS

Research article

Shangina E.I.*

ORCID: 0000-0001-5433-8400,

Ural State Mining University, Yekaterinburg, Russia

* Corresponding author (eishangina[at]yandex.ru)

Abstract

Traditionally, when designing the slopes of railway tracks and highways, special surfaces are used. Such surfaces must meet certain engineering and technological requirements. From a geometric point of view, these surfaces are most often linear and cylindrical surfaces. The current article presents an overview of Catalan surfaces, their application in architecture, demonstrates examples in nature, and also develops an algorithm for constructing ruled surfaces, in particular, the surface of an equidistant slope and the surface of the same slope. The application value of these surfaces lies in the fact that these surfaces can be geometric models of road slopes.

Keywords: geometric modeling, road slopes, ruled surfaces, Catalan surfaces.

Введение

Проектирование таких сложных технических сооружений, как железнодорожные пути, автомобильные дороги, всегда было непростым процессом, требующим всестороннего анализа самых разных параметров. В современном мире дороги должны иметь хорошие транспортно-эксплуатационные и функциональные характеристики, обеспечивать высокую безопасность движения. В этих условиях решающую роль играет выбор технологий, инструментов, а главное методов, используемых для проектирования.

При проектировании откосов железнодорожных путей и автомобильных дорог используются разные поверхности. Такие поверхности должны удовлетворять определенным инженерным требованиям. С геометрической точки зрения эти поверхности, чаще всего представляют собой линейчатые поверхности. Линейчатые поверхности образованы движением прямой (образующей) по заданному закону. Закон ее движения обычно задается тремя направляющими. Если одна из направляющих будет являться несобственной (бесконечно удаленной), а две другие действительными, такие поверхности называются поверхностями с плоскостью параллелизма. Также эти поверхности называют поверхностями Каталана [1], [2], [3]. К таким поверхностям, например, относятся поверхность равнодлинного откоса и поверхность одинакового ската. Эти поверхности уменьшают возможность снежных заносов и воздушных завихрений. Кроме поверхностей Каталана применяется также и цилиндрическая поверхность. Полотно дороги в поперечном сечении выполняется в виде дуги окружности (а не в виде прямой) с целью повышения устойчивости транспортных средств и с целью улучшения стока воды.

Современные методы проектирования дорог

В настоящее время железнодорожные пути и автомобильные дороги проектируются с помощью систем автоматизированного проектирования (CAD/CAM/CAE). Автоматизированное проектирование позволяет разработать и выпустить проектную документацию. Процесс проектирования можно разбить на следующие основные этапы:

1) разработка цифровой модели рельефа (ЦМР);

2) определение трассы дороги в плане и профиле;

3) трехмерное моделирование дороги;

4) расчет объемов работ и создание проектно-сметной документации.

Рассмотрим первые три этапа проектирования дорог. Цифровая модель рельефа получается на основе точных данных о местности. Цифровая модель рельефа — это математическое представление участка земной поверхности, полученное путем обработки материалов топографической съемки. Наиболее используемыми методиками получения высотных отметок являются топографическая съёмка местности, радарная съёмка. Цифровая модель позволяет не просто посмотреть положение одного объекта относительно другого, но и уточнить структуру исследуемого объекта, а также просчитать объект. Традиционно для получения цифровой модели рельефа предварительно необходимо было проводить геодезическую съемку, которая включала в себя работу огромного количества специалистов, приборов и др. Эта ситуация усугублялась в условиях замеров крупных территорий. За счет этого процедура была не только дорогостоящей, но и отнимала много времени, замедляя общий ход работ. Сегодня для сбора информации используются беспилотники – квадрокоптеры.

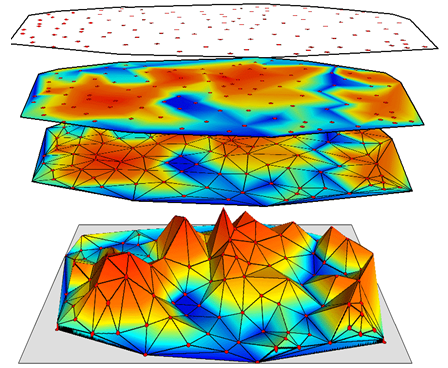
Алгоритм моделирования цифровой модели рельефа заключается в следующем (рис. 1). Во-первых, необходимо подобрать беспилотник, составить карту полетов в зависимости от величины территории и структуры объекта. Во-вторых, расставляется необходимое количество опорных точек. Затем квадрокоптер пролетает по заранее построенному маршруту и считывает координаты опорных точек. В-третьих, все полученные материалы передаются специалистам, которые разрабатывают на их основе цифровую модель рельефа. Цифровая модель рельефа конструируется с использованием профессионального программного обеспечения. Этот метод позволяет в разы ускорить подготовку и проведения съемки и получить достаточные данные для построения цифровой модели рельефа [4].

Рис. 1 – Алгоритм моделирования цифровой модели рельефа

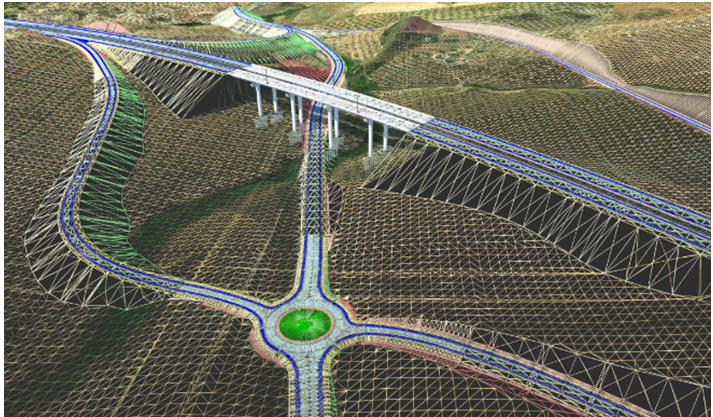
Рис. 2 – Цифровая модель рельефа и трехмерная модель дороги

 

Трехмерное моделирование трассы дороги определяет ее протяженность, размещение дорожных сооружений и капитальных объектов, стоимость выполнения строительных работ, функциональные особенности движения транспорта и др. (рис. 2). Возможности автоматизированного проектирования позволяют оперативно и качественно проработать множество вариантов моделей будущей трассы. Кроме этого, положение трассы конструируется с учетом рельефа местности. По данным топографической съемки рельефа и на базе анализа геологических, гидрологических и метеорологических критериев моделируется ось будущей дороги.

Трехмерное моделирование дороги начинается с определения типовых поперечных профилей (конструкций). Конструкции собираются из элементов, присоединяемых к базовой линии трассы. Базовая линия трассы в поперечном профиле конструируется в виде дуги окружности (а не в виде прямой) с целью повышения устойчивости транспортных средств и с целью улучшения стока воды. Затем к базовой линии трассы присоединяются откосы, которые представляют собой сложные линейчатые поверхности. Откосы должны обладать некоторыми технологическими характеристиками. Например, с целью плавного сопряжения рельефа и откоса на участках насыпи или выемки дороги должна быть постоянная длина или одинаковый уклон. Рассмотрим моделирование таких поверхностей.

Геометрические методы проектирования откосов дорог

При формировании линейчатой поверхности с помощью плоскости параллелизма образующие должны быть параллельны этой плоскости. Поэтому эти образующие пересекаются с ней в несобственных точках, множество которых определяет несобственную прямую. Эту прямую следует рассматривать как третью направляющую линейчатой поверхности. Другими словами, плоскость параллелизма является собственным представителем несобственной прямой. Такие линейчатые поверхности с плоскостью параллелизма называются поверхностями Каталана [5].

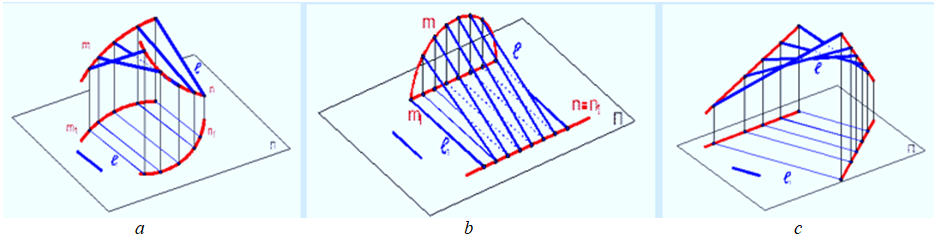
Образование поверхности Каталана является частным случаем общего способа формирования линейчатой поверхности с двумя направляющими. К поверхностям Каталана относятся следующие поверхности (рис. 3): цилиндроид, коноид, гиперболический параболоид (косая плоскость) [6].

 

Рис. 3 – Поверхности Каталана:

а – цилиндроид; b – коноид; с – гиперболический параболоид (косая плоскость)

 

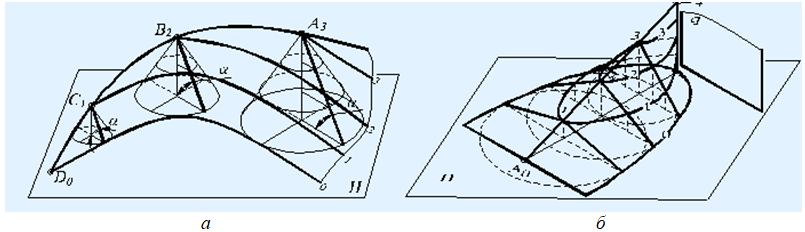
Поверхности Каталана широко используются в архитектуре и встречаются в природе (рис. 4). В данной статье нами исследуются поверхность одинакового ската и поверхность равнодлинного откоса. Эти поверхности относятся к линейчатым поверхностям (Каталана) (рис. 5).

Рис. 4 – Примеры поверхностей Каталана в архитектуре и природе

 

Поверхность одинакового ската представляет собой в пространстве огибающую множество прямых круговых конусов, вершины которых лежат на пространственной кривой.

Поверхность одинакового ската – линейчатая поверхность. Все образующие этой поверхности составляют с горизонтальной плоскостью проекций Н одинаковый угол a, равный углу наклона образующих конуса. Частным случаем этой поверхности является эвольвентная поверхность. Для построения горизонталей поверхности одинакового ската необходимо иметь проекцию кривой линии и угол наклона поверхности (образующих конуса) a к горизонту.

 

Рис. 5 – Линейчатые поверхности (поверхности Каталана):

а - поверхность одинакового ската; б - поверхность равнодлинного откоса

 

Поверхность равнодлинного откоса является линейчатой поверхностью. Образующая этой поверхности (отрезок прямой постоянной длины) перемещается в пространстве так, что его один конец скользит по направляющей (пространственной кривой/прямой линии). Другой конец образующей перемещается по заданной поверхности/плоскости, причём горизонтальная проекция образующей всегда перпендикулярна горизонтальной проекции направляющей.

Частным случаем поверхности равнодлинного откоса является такая поверхность, образующая которой (отрезок постоянной длины) одним концом скользит по прямой, а другим концом скользит по горизонтальной плоскости. В этом случае эта поверхность конструируется в виде поверхности, которая соприкасается с однопараметрическим множеством прямых круговых конусов с вертикальной осью. Вершины этих конусов лежат на направляющей (прямой), а основания – на заданной плоскости. На практике такая поверхность заменяется поверхностью, образующие которой на горизонтальной проекции перпендикулярны горизонтальной проекции направляющей (по определению). Длины образующих этих конусов, заключённых между вершинами и основаниями, равны. Однако угол наклона образующей конуса к горизонтальной плоскости проекций меняется при движении конуса вдоль направляющей.

Поверхность равнодлинного откоса такого вида конструируется следующим образом. Направляющая - отрезок прямой; образующая – отрезок прямой постоянной длины. Горизонтальные проекции образующей и направляющей перпендикулярны. Другими словами, все горизонтальные проекции образующих будут параллельны между собой, а, следовательно, параллельны плоскости параллелизма q (рис. 5, б). Образующая поверхности одним концом скользит по направляющей, другим – по горизонтальной плоскости. В результате движения образующей по горизонтальной плоскости, в пересечении получается плоская кривая, которую можно рассматривать, в данном случае как направляющую. Тогда поверхность равнодлинного откоса можно является частью коноида [7], [8]. Рассмотрим алгоритм построения этой поверхности в AutoCAD Civil 3D. Данная программа предназначена для автоматизации проектирования различных земельных сооружений, которой пользуются геодезисты, специалисты по землеустройству, проектировщики генпланов и сооружений, позволяющая динамически обновлять все связанные объекты при внесении изменений в результаты изысканий или проектные решения. Предлагаемый алгоритм может быть впоследствии заложен в эту программу.

Определителем поверхности равнодлинного откоса (части коноида) является:

1) направляющая – отрезок прямой АВ; образующая – отрезок прямой постоянной длины. Горизонтальные проекции образующей и направляющей перпендикулярны;

2) образующая поверхности (отрезок) одним концом скользит по направляющей, другим по горизонтальной плоскости Н=xOy.

В общем случае, поверхность равнодлинного откоса можно конструировать поверхностью, которая соприкасается с однопараметрическим множеством прямых круговых конусов с вертикальной осью (вершины этих конусов лежат на направляющей (прямой) АВ, а основания на горизонтальной плоскости Н). Тогда образующую конуса можно рассматривать как постоянную образующую поверхности равнодлинного откоса (части коноида).

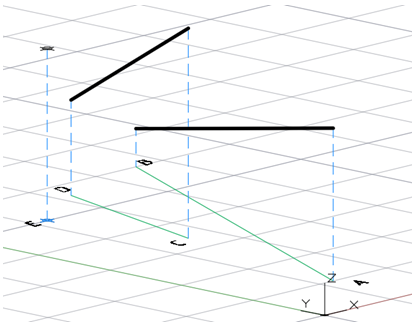
Образующая поверхности определяется прямой, проходящей через точку Е, пересекающей две скрещивающиеся прямые АВ и СD (точки А, В, С, D, Е задаются координатами x, y, z), рис.6.

Рис. 6 – Данные для определения образующей поверхности равнодлинного откоса

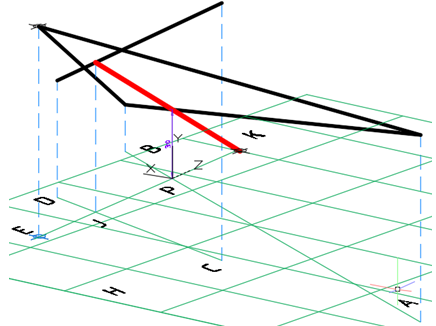
Рис. 7 – Определение образующей поверхности равнодлинного откоса

 

Известно, что через точку Е и две скрещивающиеся прямые АВ и СD проходит единственная прямая ЕР, определяемая пересечением прямой СD с плоскостью пучка прямых (точка J). Пучок прямых задаётся точкой Е и прямой АВ (рис.7). Построив прямую ЕР, находят образующую поверхности равнодлинного откоса РК. Точка К – точка пересечения прямой ЕР с плоскостью Н, т.е. определяют координату z=0 (нулевую отметку) прямой ЕР. Далее находят высотную отметку точки Р. На рис. 7 эта высотная отметка равна 30, которая определена тривиальным измерением отрезка. Если используются проекции, то эта величина определяется градуированием отрезка ЕК.

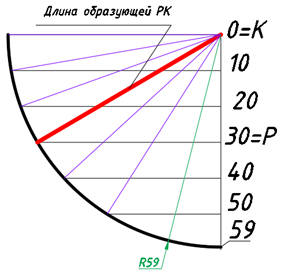
Для определения других образующих части коноида (поверхности равнодлинного откоса) проводят окружность радиуса R, равной натуральной величине отрезка образующей – прямой РК, показано на рис.8. По построению этот радиус R =59. Рассекают эту окружность горизонтальными прямыми, расстояния между которыми, в масштабе, равны единице высотного превышения – линейный масштаб (в примере линейный масштаб равен 10). Длину отрезка РК можно рассматривать как постоянную образующую конусов.

Рис. 8 – Определение угла наклона образующих поверхности равнодлинного откоса

Рис. 9 – Каркас поверхности равнодлинного откоса

 

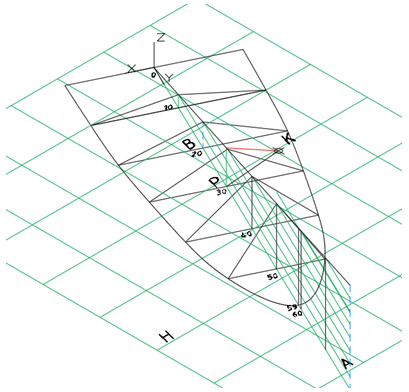
Затем строятся образующие поверхности равнодлинного откоса (части коноида) (рис.9), проходящие через отметки 0,10,20,30, причём горизонтальные проекции этих образующих на плане перпендикулярны направляющей АВ. В точке с отметкой 59 образующая поверхности будет вертикальной.

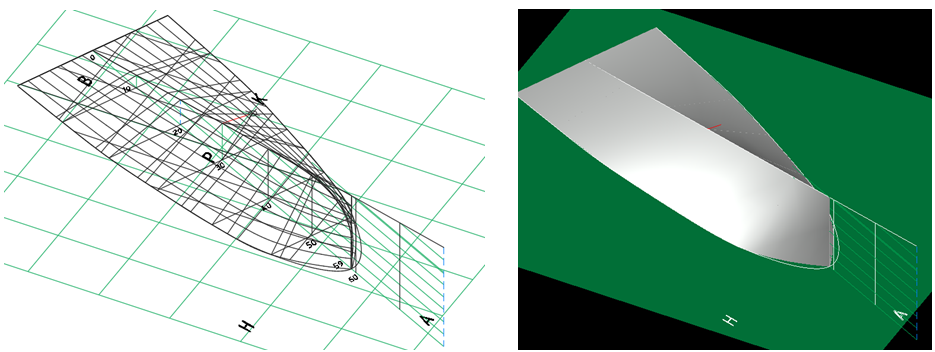
В результате лофтингового моделирования поверхность равнодлинного откоса представлена на рис. 10 в каркасном и реалистичном изображении.

Рис. 10 – Модель поверхности равнодлинного откоса в каркасном и реалистичном изображении

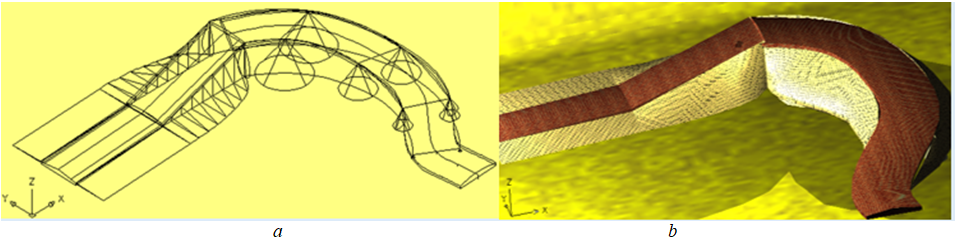
  Выводы

Проведен подробный анализ поверхностей Каталана с точки зрения прикладного значения в использовании моделирования откосов дорог. Представлены решения в моделировании откосов дорог методами линейчатой геометрии (рис.11). Получены необходимые и достаточные условия, отделяющие этот класс поверхностей Каталана от класса линейчатых поверхностей.

 

Рис. 11 – Модели откосов дорог, с различными линейчатыми поверхностями:

а - каркасное изображение поверхностей; b - реалистичное изображение поверхностей

Конфликт интересов Не указан.

Conflict of Interest None declared.

Список литературы / References

1. Salomon D. Curves and Surfaces for Computer Graphics / D. Salomon, Springer, 2006.
2. Бабич В. Н. Геометрическое моделирование алгебраических объектов / В. Н. Бабич, Е. И. Шангина // VIII Международная научно-техническая конференция «Инновационные геотехнологии при разработке рудных и нерудных месторождений», г. Екатеринбург, 4-5 апреля 2019 г. (Уральская горнопромышленная декада, г. Екатеринбург, 3-12 апреля 2019 г.): сборник докладов / Оргкомитет: Н. Г. Валиев (отв. за выпуск) и др.; Урал. гос. горный ун-т. – Екатеринбург: Изд-во УГГУ, 2019. – С. 256-261.
3. Волков В.Я. Теория параметризации и моделирования геометрических объектов многомерных пространств и её приложения / В.Я. Волков. Автореферат докт. дисс. – М.: 1983.
4. Shangina E.I. Geometric Modeling of a Topographic Surface Based on a Fractal Coordinate System / E.I. Shangina // ICGG 2020—Proceedings of the 19th International Conference on Geometry and Graphics—San-Paolo, Brazil, January 18–22, 2021, p. 2034.
5. Гордон В. О. Курс начертательной геометрии: учебное пособие для втузов / В. О. Гордон, М. А. Семенцов-Огиевский. – М.: Наука, 2007 –271 с.
6. Фролов С. А. Начертательная геометрия: учебник / С. А. Фролов. – 3 изд. перераб. и доп. – М.: ИНФРА – М, 2008 – 281 с.
7. Шангина Е.И. Геометрическое конструирование многообразий графическими методами применительно к процессам обогащения.: дисс. ... канд. техн. наук: 05.01.01 / Елена Игоревна, Шангина – М, 2010. – 159 с.
8. Шангина. Е.И. Геометрические принципы формирования поверхностей на основе движений / Е.И. Шангина. // Технологии, машины и производство лесного комплекса будущего. Материалы Международной научн.-практич. конф., посвященной 50-летию лесоинженерного факультета. Воронеж: Изд-во ВГЛА, 2004 - С. 42-46.

Список литературы на английском языке / References in English

1. Salomon D. Curves and Surfaces for Computer Graphics / D. Salomon, Springer, 2006.
2. Babich V. N. Geometricheskoe modelirovanie algebraicheskikh ob"ektov. VIII Mezhdunarodnaja nauchno-tekhnicheskaja konferencija «Innovacionnye geotekhnologii pri razrabotke rudnykh i nerudnykh mestorozhdenijj», g. Ekaterinburg, 4-5 aprelja 2019 g. (Ural'skaja gornopromyshlennaja dekada, g. Ekaterinburg, 3-12 aprelja 2019 g.) [Geometric Modeling of Algebraic Objects. VIII International Scientific and Technical Conference "Innovative Geotechnologies in the Development of Ore and Non-Metallic Deposits", Yekaterinburg, April 4-5, 2019 (Ural Mining and Industrial Decade, Yekaterinburg, April 3-12, 2019): A Collection of Reports] / V. N. Babich, E. I. Shangina / Organizing Committee: N. G. Valiev et al.; . - Yekaterinburg: Ural State Mining University Publishing House, 2019, pp. 256-261 [in Russian]
3. Volkov V. Ya. Teorija parametrizacii i modelirovanija geometricheskikh ob"ektov mnogomernykh prostranstv i ejo prilozhenija [The Theory of Parametrization and Modeling of Geometric Objects of Multidimensional Spaces and Its Applications]. Extended abstract of Doctor's thesis / V. Ya. Volkov. - Moscow: 1983 [in Russian]
4. Shangina E.I. Geometric Modeling of a Topographic Surface Based on a Fractal Coordinate System / E.I. Shangina // ICGG 2020—Proceedings of the 19th International Conference on Geometry and Graphics—San-Paolo, Brazil, January 18–22, 2021, p. 2034.
5. Gordon V. O. Kurs nachertatel'nojj geometrii: uchebnoe posobie dlja vtuzov [Course of Descriptive Geometry: A Textbook for Vtuzov] / V. O. Gordon, M. A. Sementsov-Ogievsky. - M.: Nauka, 2007, 271 p. [in Russian]
6. Frolov S. A. Nachertatel'naja geometrija: uchebnik [Descriptive Geometry: A Textbook] / S. A. Frolov. - 3rd edition. Revised and Expanded - M.: INFRA-M, 2008, 281 p. [in Russian]
7. Shangina E. I. Geometricheskoe konstruirovanie mnogoobrazijj graficheskimi metodami primenitel'no k processam obogashhenija [Geometric Construction of Manifolds by Graphical Methods in Relation to Enrichment Processes]: Candidate's thesis. Engineering Sciences: 05.01.01 / Elena Igorevna, Shangina-M, 2010. - 159 p. [in Russian]
8. E. I. Geometricheskie principy formirovanija poverkhnostejj na osnove dvizhenijj. Tekhnologii, mashiny i proizvodstvo lesnogo kompleksa budushhego. Materialy Mezhdunarodnojj nauchn.-praktich. konf., posvjashhennojj 50-letiju lesoinzhenernogo fakul'teta [Geometric Principles of Forming Surfaces Based on Movements. Technologies, Machines and Production of the Forest Complex of the Future. Proceedings of the International Scientific and Practical Conference Dedicated to the 50th Anniversary of the Faculty of Forest Engineering] / E. I. Shangina. Voronezh: Publishing House of the Voronezh State Forestry Academy, 2004, pp. 42-46  [in Russian]