ВОЛНОВАЯ ДИНАМИКА ЭКСПОНЕНЦИАЛЬНО СТРАТИФИЦИРОВАННЫХ СРЕД

Булатов В.В.¹, Владимиров Ю.В.²

¹ORCID:  0000-0002-4390-4013, Доктор физико-математических наук, ²ORCID: 0000-0002-2139-5078, Кандидат физико-математических наук, Институт проблем механики им.А.Ю.Ишлинского РАН

ВОЛНОВАЯ ДИНАМИКА ЭКСПОНЕНЦИАЛЬНО СТРАТИФИЦИРОВАННЫХ СРЕД

Аннотация

В статье рассмотрены вопросы, связанные с динамикой  внутренних гравитационных волн в экспоненциально стратифицированных средах бесконечной глубины. Обсуждаются адекватность и пределы применимости используемой модели стратифицированной среды, а также основные качественные особенности динамики плоских волновых пакетов внутренних гравитационных волн. Показано что  как минимум в двух отношениях, внутренние гравитационные волны в безграничной экспоненциально стратифицированной среде качественно отличаются акустических и электромагнитных колебаний: частоты колебаний распространяющихся внутренних волн не могут превосходить частоту плавучести, и внутренние гравитационные волны распространяются не по нормали к волновым фронтам.

Ключевые слова: внутренние гравитационные волны, динамика стратифицированной среды, частота плавучести, волновой фронт.

Bulatov V.V.¹, Vladimirov Yu.V.²

¹ORCID:  0000-0002-4390-4013, PhD in Mathematics, ²ORCID: 0000-0002-2139-5078, PhD in Mathematics, Institute for Problems in Mechanics RAS (Moscow)

WAVE DYNAMICS OF  EXPONENTIALLY STRATIFIED MEDIUM

Abstract

The problems of internal gravity waves dynamics in unbounded exponentially stratified medium are considered. We discuss the relevance and limits of applicability of the used  stratified medium model. The basic qualitative features of the internal gravity waves plane  packets dynamics are obtained. It is shown that internal gravity waves in an unbounded exponentially stratified medium qualitatively differ from acoustic and electromagnetic oscillations. The frequency of propagating internal waves oscillations  can not exceed the buoyancy frequency. Internal gravity waves propagate not along the normal to the wave fronts.

Keywords: internal gravity waves, stratified medium dynamics, buoyancy frequency, wave front.

В настоящей работе рассмотрены особенности волновой динамки внутренних гравитационных волн в безграничной экспоненциально стратифицированной среде. Вначале сделаем несколько замечаний об адекватности моделей стратифицированных сред, в которой распространяются колебания. Простейшей моделью природной стратифицированной среды является безграничная по вертикали экспоненциальная среда, т. е. среда, в которой невозмущенная плотность  экспоненциально зависит от z: . Для такой среды линеаризованная система уравнений внутренних волн сводится к системе с постоянными коэффициентами, и её решение можно получить методом Фурье, хотя вычисление асимптотики волнового поля вдали от источника возмущений, равномерной по координатам точки наблюдения представляет собой достаточно сложную, но вполне решаемую аналитическую задачу [1-7]. Однако соответствие качественных свойств дальних полей в экспоненциальной безграничной по вертикали среды, полученных  на основе асимптотических аналитических оценок, реальной волновой картине в океане требует, по всей видимости,  дополнительного физического обоснования. Как правило, в океанических условиях распространение внутренних волн происходит в слое конечной толщины (толщины слоя скачка плотности), т.е. порядка 50-100 метров, и лишь в океане, где имеются два термоклина - сезонный и главный, толщина слоя имеет порядок одного километра и более. В то же время, как правило, представляет интерес распространение волн на дистанциях порядка десятков километров, т.е. на дистанциях, превышающих на один или два порядка толщину стратифицированного слоя. Ясно, что в этой ситуации заменять слой конечной толщины на безграничную по вертикали среду неправомерно. Дальнее поле в безграничной по вертикали среде и в слое конечной толщины имеют два качественно общих свойства: в обеих задачах поле при удалении от источника убывает, впрочем, характер убывания различен, и в обеих задачах имеются области, где поле имеет осциллирующий, волнообразный характер, однако эти пространственные области существенно различаются [1-4]. При решении полной системы нелинейных уравнений гидродинамики, и в дальнейшем отщеплении линейной части решения в процессе численного расчета зон перемешивания, турбулентных следов, различных вихревых образований  и возбуждаемых ими внутренних гравитационных волн модель экспоненциальной безграничной среды может оказаться физически вполне адекватной, т.к. основные гидрофизические процессы локализованы в относительно ограниченной пространственной области. Поэтому если найти из этих рассмотрений некоторое распределение источников возмущений, аппроксимирующее, например, турбулентный след или иные локализованные начальные неволновые возмущения, то далее можно рассчитывать по этим численным данным дальние волновые поля, уже учитывая конечную толщину стратифицированного слоя и реальное распределение невозмущенной плотности. Кроме того, модель бесконечной экспоненциально стратифицированной среды, по-видимому, является достаточно адекватной для описания полей внутренних гравитационных волн, возбуждаемых в искусственных стратифицированных средах, в том числе в лабораторных условиях [5-7].

Рассмотрим далее плоские волновые пакеты внутренних гравитационные волн в экспоненциально стратифицированной среде. Самый простой вид уравнения внутренних гравитационных волн приобретают в случае экспоненциально стратифицированной жидкости, в которой невозмущенная плотность - экпоненциальная функция глубины: . В такой среде  и основное уравнение, описывающее внутренние гравитационные волны (в приближении Буссинеска),  становится уравнением с постоянными коэффициентами

LW = 0  (1)

и система линеаризованная уравнений гидродинамик имеет вид

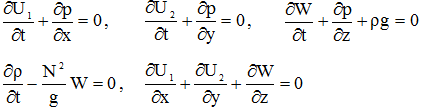  (2)

Простейшие решения этих уравнений - это плоские волны, с зависимостью от , где  - волновой вектор. Повернем оси x,y так, чтобы β обратилось в нуль, то есть чтобы рассматриваемое поле не зависело от y (тогда, в частности, ). Полагая  получим из (1) дисперсионное уравнение

  (3)

а из (2) - систему уравнений относительно

  (4)

Условие разрешимости системы (4) - выполнение дисперсионного соотношения (3). Положим . Ограничиваясь для определенности волнами, распространяющимися в положительном направлении оси x, получим (U - постоянный амплитудный множитель)

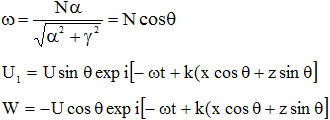  (5A)

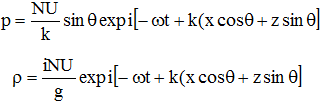  (5B)

Прокомментируем выписанные соотношения. Частота колебаний ω не зависит от модуля k волнового вектора, определяется лишь его направлением и не превосходит частоты плавучести N. Максимальное значение ω приобретает при θ = 0, в этом случае: ,

, то есть волновой вектор направлен по горизонтали, а среда испытывает лишь вертикальные колебания. При  в пределе ω = 0, и мы получаем стационарное движение, в котором: , то есть имеется сдвиговое горизонтальное течение с гармонической зависимостью от z и возмущение плотности (с соответствующим ему возмущением давления) с той же зависимостью от z. Заметим, что для волнового уравнения и системы уравнений Максвелла дисперсионное уравнение имеет вид , то есть ω, наоборот, не зависит от направления волнового вектора и определяется лишь его длиной. Из последнего уравнения в (4) следует, что вектор скорости  перпендикулярен волновому вектору (α,β), то есть что вектор скорости направлен вдоль волновых фронтов - линий постоянной фазы . Поэтому, казалось бы, внутренние гравитационные волны, подобно уравнениям Максвелла (где для плоской волны векторы E и H также направлены вдоль волновых фронтов), являются поперечными волнами. Однако, такое заключение преждевременно. Согласно общей теории колебаний в средах с дисперсией, вектор групповой скорости, то есть скорости движения волновых пакетов с высокочастотным заполнением, определяется соотношением

  (6)

где  вычисляются из дисперсионного соотношения (5А)

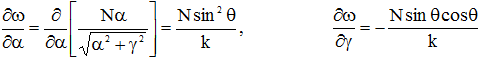
Откуда видно, что направление вектора групповой скорости совпадает с направлением вектора . То же направление имеет среднее за период  значение вектора плотности потока энергии . При вычислении  следует учесть, что физический смысл имеют не комплексные функции (5В), а их вещественные части

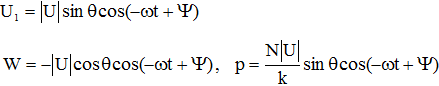  (7)

где  и при вычислении потока энергии надо в качестве  брать выражения (7).

К аналогичному направлению распространения можно прийти, если искать решения этих уравнения  лучевым методом (методом геометрической оптики), то есть строить для внутренних волн аналог ВКБ решения для волнового уравнения или уравнений Максвелла.         Проведенный анализ показывает, что  как минимум в двух отношениях, внутренние гравитационные волны в безграничной экспоненциально стратифицированной среде качественно отличаются акустических и электромагнитных колебаний. Во-первых, частоты колебаний распространяющихся внутренних волн не могут превосходить частоту плавучести , и во-вторых, внутренние гравитационные волны распространяются не по нормали к волновым фронтам. Работа выполнена при частичной поддержке РФФИ (проект 17-01-00010).

Список литературы / References

1. Bulatov V.V. Internal gravity waves: theory and applications / V.V.Bulatov, Yu.V.Vladimirov. - Moscow: Nauka Publishers,  2007. - 304 p.
2. Булатов В.В. Динамика негармонических волновых пакетов в стратифицированных средах / В.В.Булатов, Ю.В.Владимиров. - М.: Наука, 2010. - 470 с.
3. Bulatov V.V. Wave dynamics of stratified mediums / V.V.Bulatov, Yu.V.Vladimirov. - Moscow: Nauka Publishers, 2012. - 584 p.
4. Булатов В.В. Волны в стратифицированных средах / В.В.Булатов, Ю.В.Владимиров. - М.: Наука, 2015. - 735 с.
5. Sutherland B.R. Internal gravity waves / B.R.Sutherland. - Cambridge: Cambridge University Press, 2010. - 394 p.
6. Miropol'skii Yu.Z. Dynamics of internal gravity waves in the ocean /Yu.Z.Miropol'skii, O.V.Shishkina. - Boston: Kluwer Academic Publishers, 2001. - 421 p.
7. Pedlosky J. Waves in the ocean and atmosphere: introduction to wave dynamics / J.Pedlosky. -  Berlin–Heidelberg: Springer, 2010. - 260 p.

Список литературы на английском языке / References in English

1. Bulatov V.V. Internal gravity waves: theory and applications / V.V.Bulatov, Yu.V.Vladimirov. - Moscow: Nauka Publishers,  2007. - 304 p.
2. Bulatov V.V. Dinamika negarmonicheskih volnovih paketov v stratificirovannih sredah [Non-harmonic wave packets dynamics in stratified medium] / V.V.Bulatov, Yu.V.Vladimirov. - M.: Nauka, 2010. - 470 p. [in Russian]
3. Bulatov V.V. Wave dynamics of stratified mediums / V.V.Bulatov, Yu.V.Vladimirov. - Moscow: Nauka Publishers, 2012. - 584 p.
4. Bulatov V.V. Volni v stratificirovannih sredah [Waves in stratified medium] / V.V.Bulatov, Yu.V.Vladimirov. - M.: Nauka, 2015. - 735 p. [in Russian]
5. Sutherland B.R. Internal gravity waves / B.R.Sutherland. - Cambridge: Cambridge University Press, 2010. - 394 p.
6. Miropol'skii Yu.Z. Dynamics of internal gravity waves in the ocean /Yu.Z.Miropol'skii, O.V.Shishkina. - Boston: Kluwer Academic Publishers, 2001. - 421 p.
7. Pedlosky J. Waves in the ocean and atmosphere: introduction to wave dynamics / J.Pedlosky. -  Berlin–Heidelberg: Springer, 2010. - 260 p.