ВЛИЯНИЕ ТОПОЛОГИИ МИОКАРДА СЕРДЦА НА НАПРЯЖЕННОСТЬ МАГНИТНОГО ПОЛЯ, ИЗМЕРЯЕМОГО МАГНИТОКАРДИОГРАФОМ

Арутюнов Ю. А.¹, Возовиков И.Н.², Дробязко А.А.³, Шашок П.А.³, Чащин Е.А.⁴

¹Кандидат физико-математических наук, Ведущий научный сотрудник, Научно-клинический центр спортивной медицины федерального медико-биологического агентства России, ²Доктор медицинских наук, Профессор, Центральная клиническая больница восстановительного лечения федерального медико-биологического агентства России, ³Инженер, ООО «Двойная спираль», ⁴Кандидат технических наук, Заведующий кафедрой «Электротехника», Ковровская государственная технологическая академия им.В.А. Дегтярева

ВЛИЯНИЕ ТОПОЛОГИИ МИОКАРДА СЕРДЦА НА НАПРЯЖЕННОСТЬ МАГНИТНОГО ПОЛЯ, ИЗМЕРЯЕМОГО  МАГНИТОКАРДИОГРАФОМ

Аннотация

Одним из распространенных заболеваний сердечно-сосудистой системы животных является развитие патологии, сопровождающейся возникновением дистрофических и деструктивных изменений в миокарде сердца. Результаты современных исследований показали, что характеристики гемодинамики, физико-механики и электрофизики сердечно сосудистой системы, близкие к результатам физиологических экспериментов достигаются в приближении, что миокард сердца имеет топологию Мебиуса. В приближении гипотезы о влиянии топологии магнитопровода на его приведенные характеристики, в области малых интенсивностей магнитных полей, сопоставимых с влиянием собственной намагниченности структуры, миокард сердца рассмотрен как совокупность магнитных доменов, которые связывают микроскопические магнитные характеристики с макроскопическими свойствами. Показана качественная возможность, в целях диагностики и прогнозирования развития патологий в сердечно сосудистой, системе характеризовать функциональный статус миокарда по результатам измерения напряженности магнитного поля.

Ключевые слова: миокард сердца, топология Мебиуса, магнитопровод, магнитное поле.

Arutyunov Yu.A.¹, Vozovikov I.N.², Drobyazko A.A.³, Shashok P.A.³, Chaschin Ye.A.⁴

¹PhD in Physics and Mathematics, Leading Researcher, Scientific-Clinical Center of Sports Medicine Federal Medical-Biological Agency of Russia, ²MD, Professor, Central Clinical Hospital of Regenerative Treatment Federal Medical-Biological Agency of Russia, ³Engineer, LLC « Double spiral », ⁴PhD in Engineering, Head of the Department of «Electrotechnics», Kovrov State Technical Academy

THE INFLUENCE OF THE CARDIOMUSCULAR TOPOLOGY ON THE MAGNETIZING FORCE MEASURED BY MAGNETOCARDIOGRAPH

Abstract

One of the most common diseases of the cardiovascular system of animals is the development of pathology, accompanied by the appearance of dystrophic and destructive changes in the myocardium of the heart. The results of modern studies have shown that hemodynamic characteristics, physical and mechanical and Electrophysics of cardiovascular system, similar to the results of physiological experiments, achieved in the approximation that the myocardium of the heart has a Möbius topology. The myocardium of the heart is viewed as a collection of magnetic domains that connect microscopic magnetic characteristics with macroscopic properties. It was done in the approximation of the hypothesis of the influence of the magnetic topology on its given characteristics in the low intensities of magnetic fields comparable to the effect of its own magnetization of the structure. Qualitative possible to characterize the functional status of the myocardium by measuring the magnetizing force for the purpose of diagnostics and prediction of the pathologies evolution of cardio-vascular system has been shown.

Keywords: heart myocardium, mobius topology, magnetic circuit, magnetic field.

Introduction

It is known that the cardiovascular system is one of the most important systems of animals organism. Animals often suffer from various heart diseases. One of the most common diseases of the cardiovascular system of animals is the development of pathology, accompanied by the appearance of dystrophic and destructive changes in the myocardium of the heart. The results of modern researches have shown that the characteristics of hemodynamics, physicomechanics and electrophysics of the cardiovascular system, close to the results of physiological experiments, are achieved in the approximation that the myocardium of the heart has the Mobius topology [1, 2].

In the modern methodology for the analysis of complex systems, it is proposed to draw analogies between processes that relate to different fields of science. It is done by considering of dynamic models and constructing of general laws of behavior and management, with the aim of finding new regularities and characteristics of a complex system. In particular, this applies to Mobius transformations, which occupy a special place, since they represent a composition of a finite number of inversions relative to spheres in Euclidean space . Moreover, the group of all Mobius transformations of the space  is finite-dimensional, and its subgroup, which is composed of orientation-preserving mappings, is isomorphic  [3]. The lattest statement has a particular interest during the construction of a mathematical model that describes the propagation of the magnetic field produced by ferrimagnetic materials when the geometric parameters of the magnetic circuit are changed, in particular when it is transformed in the form of a Mоbius loop. It makes relevant the solution of the task of "visualizing" the internal structure of the myocardium of the heart.

Material and methods

It is known that ferromagnetic materials have a domain structure, whose orientation determines the magnitude of the remanent magnetization of the magnetic circuit. We assume that in a magnetic circuit with lumped electromagnetic coils there are several magnets arranged so that the distances between them are large in comparison with their dimensions. In this approximation, we can assume that the field configuration will be similar to the field pattern created by electric dipoles [4]. We assume that these magnetic dipoles are formed by fictitious magnetic charges ±m_i, the distance between them is l_i. It is known that a single magnetic dipole creates a magnetic field, which is analogous to the field of an electric dipole [5]. In this approximation, the magnetostatic interaction of individual components within the volume of a magnetized solid reduses to the generation of its own magnetostatic energy, the magnitude of which can be determined as

  (1)

where Ф_i is a magnetic potential created by all charges except i-th at the location of the i-th charge. If we assume that the magnetic charges are distributed in a space with density ρ, then expression (1) can be conveniently written as

   (2)

where V is a volume of a magnetic material. We rewrite expression (2) in accordance with the known recommendations [4]:   (3)

It can be seen that for a space filled with a magnetic material with magnetization J_S, the magnetostatic interaction of individual volume elements inside a magnetized solid leads to the presence of the magnetostatic energy of this solid. And the value of the extraneous field H_m leads to the formation of spontaneous magnetization regions, that is, to the formation of a domain structure. Thus, when modeling the magnetic field produced by a toroidal magnetic core with the Mobius topology, we shall assume that the magnetization processes and magnetization reversal processeses are determined by the properties of the domain structure. For the estimation of the influence of an nonoriented surface on the propagation of a magnetic field in its volume, we take that the anisotropy energy and exchange interactions energy are negligibly small. We also neglect the domain-wall thickness. Taking into account the simplifications made, we assume that in the design model the magnetic circuit (Fig. 1, pos. 1) is made of a ferromagnetic material in the form of a torus with a Mobius surface and a local arrangement of the magnetization coil (Fig. 1, pos. 2).

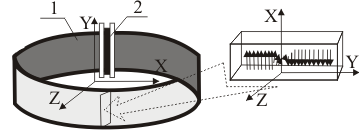
Fig. 1 - Model of the magnetic circuit

 

It is known that ferrimagnetic solids consist of regions of spontaneous magnetization, which magnetization vectors direct in different directions. Moreover, the system will have a minimum of energy if the regions will magnetically antiparallel. However, if the ferromagnetic solid is placed in an external magnetic field during the power connection to the magnetization coil, than the magnetization vectors become parallel under the action of this field [5]. So as a working hypothesis, we assume that when the magnetic field propagates in a magnetic circuit, the magnetization vectors direct in one direction and "mechanically" change their direction as the "Mobius spin zone" passes.

Let us carry out an experimental test of the hypothesis of the influence of the Möbius topology on the propagation of a magnetic field in a magnetic guide. We do this on the simulation samples. We estimate the effect of the topology of the magnetic circuit in the frequency range 50-15000 Hz, relying on the well-known method [6-9]. Determination of the comparative characteristics of electromagnetic properties is carried out according to the substitution scheme (fig. 2).

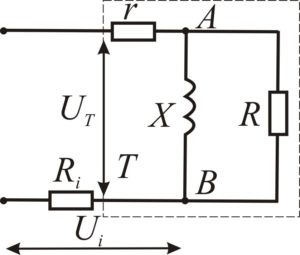
Fig. 2 - Design electric scheme of the experiment

  In the approximation of the design scheme we have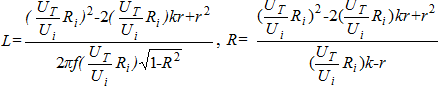   (1)

where L, R are inductive and active components of the magnetization coil with a core of various topological form (fig. 2); U_i is a voltage on the instrument resistor , which is numerically equal to the current through a magnetizing coil; U_T is an effective value of voltage on the coil; r is an active resistance of the magnetizing winding of the coin;  is a power factor of the coil, that depends on the frequency f and the phase shift τ.

  (2)

where ΔL , ΔR are the change in the inductive and active components of the magnetization coil with a core of various topological shapes; R_K, R_M is an active component of resistance in coil loss, L_K, L_M is an inductive component of resistance in coil loss, index K means the control sample of standard execution, as at usual cores; index М means an experimental sample with a Mobius topology. (see. fig. 2).

The magnitude of the relative change in the induction of saturation of the toroidal core with the Mobius topology in comparison with the induction of saturation of the control core is conveniently estimated as:

  (3)

where  is a saturation induction of the Mobius core,  is a saturation induction of the control core.

The magnitude of the relative change in residual induction depends on the amplitude of the magnetizing current and in the range of the initial section of the main magnetization curve can be determined from expression:

  (4)

where   is a residual magnetic induction of the Mobius core.

Similarly, the magnitude of the relative change in coercive force and magnetic permeability can be determined as:

  (5)

   (6)

where  is a coercive force of the Mobius core,  is a coercive force of the control core,  is a relative permeability of the Mobius core, is a relative permeability of the control core.

Results

The results of the research of the influence of the topology of the magnetic circuit on the change in the active and inductive component of the loss level are shown in Fig. 3.

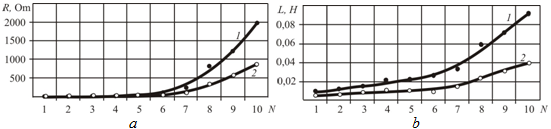
Fig. 3 - Dependence of the change in the active (a) and inductive (b) components of the resistance of the reference magnet coil at I = 0.005 A: 1 – a sample series A; 2 – a sample series В; N – the frequency equal to: 1 – 50 Hz, 2 – 100 Hz, 3 – 250 Hz, 4 – 500 Hz, 5 – 1 kHz, 6 – 2,5 kHz, 7 – 5 kHz, 8 – 10 kHz, 9 – 12 kHz, 10 – 15 kHz

It can be seen that for equal parameters of the coils of samples A and B, the ohmic loss resistance increases approximately two times more over the entire frequency range, which is not related to the change in the volume of the magnetic circuit. The magnitude of the magnetic circuit in the samples of series A and B differs by not more than 1.25% and amounts to 24.8 × 103 mm3 and 25.1 × 103 mm3, respectively. The magnitude of the magnetic circuit in the samples of series A and B differs by no more than 1.25% and is 24.8 × 103 mm³ and 25.1 × 103 mm³, respectively. Thus, it can be assumed that a change in the loss level shows the test-sensitivity to propagate the magnetic field in the magnetic circuit. It is also clear that as the frequency increases, the levels of ohmic and reactive losses in the magnetic circuit increase.

Let us consider the influence of the topology of the magnetic circuit on the change in the active and inductive component of the loss level (Fig. 4). In samples of the A series in the Mobius design, the difference in the relative loss level compared to the base version of the same series reduces to 2 times. In particular, for a frequency of 500 Hz in a series A sample, the active series resistance differs from the base version by 4%, and for the same frequency in the B series sample the relative difference reaches 8%. Similar changes are observed for the reactive resistance. Thus, the measurement results showed the sensitivity of the change in the series resistance to the change in topology in samples of series A and B. Note that a significant difference in the change in the level of losses is achieved only at the initial stage of magnetization (current strength is 0-0.01 A) and with a further increase in the magnetomotive force, the difference caused by the change in the topology of the magnetic circuit is leveled. The results of measurements also show that, when the magnetomotive force is changed, the spin of the magnetic circuit has an ambiguous effect on the magnitude of the relative change in the level of ohmic and reactive losses.

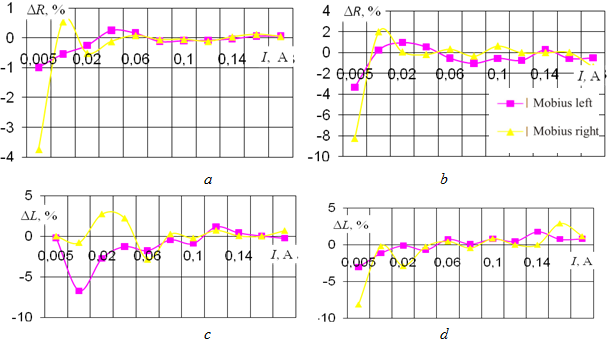
Fig. 4 - Dependence of the change in the active (a, b) and inductive (c, d) components of the resistance of the magnetizing coil at  f=500 Hz: а, b – a sample series A; c, d – a sample series В

For example, for series B (see Figure 4, d), the relative difference in the ohmic losses in the base and Mobius magnetic cores for the right spin varies from -8% to + 2% (see Fig. 4d). Similarly, for samples of the A series, the relative difference in the ohmic losses in the base and mebium magnetic cores for the left spin varies from -4% to + 0.5% at a frequency of 500 Hz. It shows the relationship with the processes of magnetic flux propagation in the magnetic circuit.

In the Fig. 5 the results of plotting the magnetization curve are given in coordinates U_X(H_max) и U_Y(B_max). It can be seen that measurements of the magnetizing coil current in the range of 50-200 mA ensure that measurements are made in all ranges of operation of the ferromagnetic magnetic core from the initial magnetization section to the saturation mode.This confirms the adequacy of the performed calculations of the parameters of the magnetization coil.

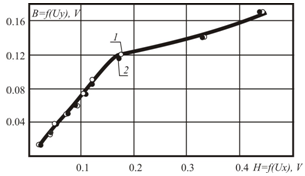
Fig. 5 - Magnetization curve: 1 – are samples of series A; 2 – are samples of the B series

 

The results of comparative studies of the influence of the Mobius topology on the magnetic properties of magnetically soft ferromagnets in a closed magnetic circuit with different topologies, which were calculated from formulas 3-6, are shown in Fig. 6-8. It can be seen that with other equal parameters of samples A and B, the change in the topology of the magnetic circuit is accompanied by the largest changes in the residual induction (see Figure 6) when working in the region of initial magnetization. In this case, an increase in the axial moment of inertia of the section of the magnetic circuit while maintaining the volume of the magnetic circuit, that is, an increase in the base of the rectangular section (see Figure 2) and a decrease in its height while maintaining the cross-section area of the yoke of the magnetic circuit, leads to a decrease in the absolute values of the "spin effect" а or a B-series sample up to 3.5% for a series A.

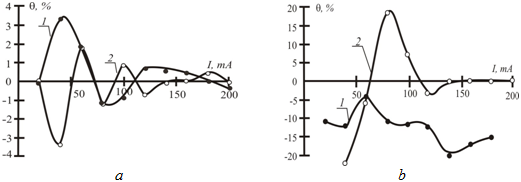
Fig. 6 - The dependence of the change in residual induction between the control and Mobius samples: a - is a sample of the A series; b - is a sample of the B series; 1 - the left spin; 2 - the right spin

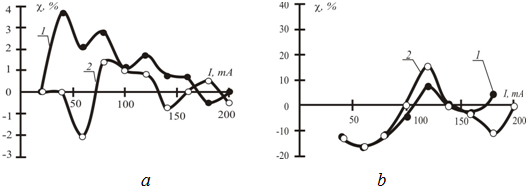
Fig. 7 - The dependence of the variation of the coercive force between the control and the Mobius samples: a - is a sample of the A series; b - is a sample of the B series; 1 - the left spin; 2 - the right spin

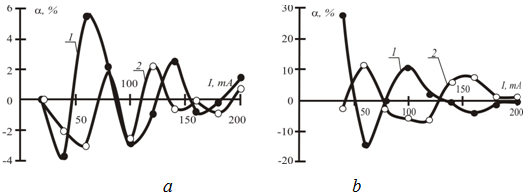
Fig. 8 - The dependence of the variation of the magnetic conductivity between the control and the Mobius samples: a - is a sample of the A series; b - is a sample of the B series; 1 - the left spin; 2 - the right spin

 

Thus, we can assume that the implementation of a magnetic circuit by a set of sheets of ferromagnetic material also does not lead to a significant increase in the coercive force of ferromagnetic toroids, as claimed by several authors [10-12]. It was confirmed by the results of the experiment (see Figure 7), which showed changes in the coercive force to 3.6% when working in the area of initial magnetization for samples of the A series, and an increase of up to 20% for the B series samples.

The results of the change in the magnetic permeability are shown in the Fig. 8. It can be seen that the dependences corresponding to the Mobius magnetic cores with right and left spins show symmetrical "mirror" deviations from the values of the magnetic permeability from the corresponding values of the control core for both sample sizes A and B. The magnetic permeability varies depending on the direction of twisting of the magnetic circuit, that is, the spin, and reaches 6% for the left and -4% for the right spins for the A-series samples and increases to 26% and 12% for the B-series samples, respectively. It is important to note that with a change in the current through the winding, the local maxima are displaced both in the magnetic cores with the left and right spins. And in all cases, a decrease in the level of losses associated with a change in the cross section of the magnetic circuit in series A leads to a decrease in the absolute values of the "spin effect".

Discussion

It is known that the active resistance should not vary significantly with the frequency change [13]. However, the obtained dependences (Fig. 4) qualitatively correspond to known experimental data [8, 9]. This shows that in the used equivalent circuit (see Fig. 2) the calculation formula (2) does not take into account the interturn capacitance of the winding. The purpose of the experiment is a relative comparison of the properties of magnetic circuits with different topologies. Therefore, the revealed problem of verification of the design scheme does not reduce the value of the experimental data shown on the graphs, and the qualitative correspondence of the behavior of the curves (see Fig. 3) of all the series of samples studied shows the reliability of the results.

The results of the investigations showed that an increase in the magnetomotive force, as well as the axial moment of inertia of the cross section of the magnetic circuit (i.e. an increase in the base of a rectangular section and a decrease in its height while maintaining the yoke cross-sectional area and the volume of the magnetic circuit) is accompanied by a decrease in the influence of the Mobius topology. The obtained results of complex studies of the physical and technical foundations of the influence of changes in the topology of the toroidal magnetic core confirm the hypothesis put forward by us: it says that the magnetization and magnetization reversal processes are determined by the properties of the domain structure as a set of regions in the magnetic subsystem of magnetic materials that connect the microscopic magnetic characteristics with their macroscopic properties and depend on the "mechanical" change in the orientation of the domains in the investigated area. Indirectly it confirmes the fact that the values of the coercive force (see Fig. 7), which are an analog of the level of losses due to hysteresis and residual induction during the changing the topology of the "mirror" deviations, do not show what the vector character of the magnetic permeability can mean, that is, do not show the dependence Its magnitude from the direction of spatial twist of the vector of magnetic induction in the core [14, 15]. Thus, an analysis of the magnetic properties of the magnetic circuit shows that the observed effects depend on the magnitude of the magnetic induction. It allows us to assume the admissibility of the hypothesis of the possibility of a "mechanical" measurement of the orientation of the domain structure of the magnetic circuit with a change in its topology when operating in the initial section of the main magnetization curve.

Conclusion

An experimental study on simulator samples was carried out in the work, and also a comparative analysis of the influence of the Möbius topology on the propagation of a magnetic field in a magnetic circuit was made. The revealed effects show that the Mobius transformation of the magnetic circuit as a composition of a finite number of inversions allows us to consider a variety of applications. Based on the current belief that the myocardium of the heart has the Mobius topology, we can assume that for each time point of the cardiocycle the result of recording the magnetic fields reflects the functional status of the myocardium from the point of view of the correspondence of the topology of the examined myocardium and the Mobius topology. Our studies confirmed the hypothesis of the influence of the Mobius topology on the propagation of a magnetic field in a magnetic circuit. It allows us to do a conclusion about the high informativeness of recording the magnetic field strength and the possibility of using it for the purposes of diagnosis and prediction of the development of pathologies in the cardiovascular system.

Список литературы / References

1. Арутюнов Ю.А. Влияние топологии Мебиуса на распространение в магнитопроводе магнитного поля [Электронный ресурс] / Ю.А. Арутюнов, И.Н. Возовиков, Е.А.Чащин, Л.И. Шеманаева // Современные проблемы науки и образования. – 2015. – № 5; URL: http://www.science-education.ru/128-22137 (дата обращения: 13.10.2015).
2. Арутюнов Ю.А. Влияние топологии магнитопровода на приведенные характеристики магнитомягких ферромагнетиков [Электронный ресурс] / Ю.А. Арутюнов, И.Н.Возовиков, Ю.В. Молокин, Е.А. Чащин, Л.И.Шеманаева // Современные проблемы науки и образования. – 2015. – № 2; URL: www.science-education.ru/129-23144(дата обращения: 26.11.2015).
3. Альфорс Л. Преобразования Мебиуса в многомерном пространстве: Пер. с англ.-М.: Мир, 1986.-112 с.
4. Тикадзуми С. Физика ферромагнетизма. Магнитные характеристики и их применения. - М.: Мир, 1987. - 420 с.
5. Бессонов Л.А. Теоретические основы электротехники. - М.: Высшая школа, 1964. - 750 с.
6. Арутюнов Ю.А. Влияние топологии магнитопровода на отклик при внешнем электромагнитном воздействии / Ю.А. Арутюнов, А.А. Дробязко, А.И. Крылов, Е.А. Чащин, П.А. Шашок, И.В. Шилов // Современные наукоемкие технологии.- 2016.- №10. -С. 29-32.
7. Арутюнов Ю.А. Сравнительный анализ влияния топологии магнитопровода на отклик при внешнем электромагнитном воздействии для магнитопровода с различными геометрическими параметрами [Электронный ресурс] / Ю.А. Арутюнов, А.А. Дробязко, А.И. Крылов, Е.А. Чащин, П.А. Шашок, А.А. Митрофанов // Интернет-журнал «НАУКОВЕДЕНИЕ».- 2017.- Том 9.- №1 http: // naukovedenie.ru/PDF/23TVN117.pdf (доступ свободный). Загл. с экрана. Яз. рус., англ.
8. Арутюнов Ю.А. Влияние топологии Мебиуса на магнитные свойства магнито-мягких ферромагнетиков в замкнутой магнитной цепи [Электронный ресурс] / Ю.А. Арутюнов, Н.П. Бадалян, А.А. Дробязко, Е.А. Чащин, П.А. Шашок // Интернет-журнал «НАУКОВЕДЕНИЕ».-2017.- Том 9.- №1 (2017) http: // naukovedenie.ru/PDF/53TVN117.pdf (доступ свободный). Загл. с экрана. Яз. рус., англ.
9. Арутюнов Ю.А. Влияние топологии листа Мебиуса на магнитные характеристики поля вне магнитопровода / Ю.А. Арутюнов, И.Н. Возовиков, А.А. Митрофанов, Е.А. Чащин, Л.И. Шеманаева, С.Н. Живаев // Современные наукоемкие технологии.- 2016.- №7.- С. 9-14.
10. Евстигнеев Н.М. Некоторые соотношения на проводнике в виде листа Мебиуса /Н.М. Евстигнеев, О.И. Рябков, И.М. Шахпаронов, С.И. Лавров // Естественные и технические науки. – 2011.- №6.- С. 50-58.
11. Меньших О.Ф. Способ косокругового намагничивания ферромагнитного тороида, Патент РФ №2391730, опубл. в бюлл. №16 от 10.06.2010.
12. Меньших О.Ф. Способ получения энергии и устройство для его реализации, Патент РФ №2332778, опубл. в бюлл. №24 от 17.08.2008.
13. Налимов В.В. Теория эксперимента.- М.: наука, 1971. – 208 с.
14. Вонсовский С.В. Магнетизм. Магнитные свойства диа-, пара-, ферро-, антиферро-, и ферримагнетиков. - М.: Наука, 1971. - 805 с.
15. Harrison R. G. Variable-domain-size theory of spin ferromagnetism // IEEE Trans. Magn. 2004. Vol. 40. № 3. P. 1506-1515.

Список литературы на английском языке / References in English

1. Arutyunov Yu.A. Vliyanie topologii Mebiusa na rasprostranenie v magnitoprovode magnitnogo polya [Influence möbius topology for distribution in magnetic circuit of a magnetic field] [Electronic resource] / Yu.A. Arutyunov, I.N.Vozovikov, Ye. A. Chaschin, L.I. Shemanaeva // Sovremennye problemy nauki i obrazovaniya [Modern problems of science and education]. – 2015. – № 5; URL: http://www.science-education.ru/128-22137 (data obrashcheniya: 13.10.2015). [in Russian]
2. Arutyunov Yu.A. Vliyanie topologii magnitoprovoda na privedennye kharakteristiki magnitomyagkikh ferromagnetikov [The influence of the topology of the magnetic circuit on the characteristics of the soft magnetic ferromagnets] [Electronic resource] / Yu.A. Arutyunov, I.N. Vozovikov, Yu.V. Molokin, Ye. A Chaschin, L.I. Shemanaeva // Sovremennye problemy nauki i obrazovaniya [Modern problems of science and education]. – 2015. – № 2; URL: www.science-education.ru/129-23144 (data obrashcheniya: 26.11.2015). [in Russian]
3. Ahlfors L. Preobrazovaniya Mebiusa v mnogomernom prostranstve: Per. s angl [Mobius transformations in several dimensions]. -M.: Mir, 1986.-112 p. [in Russian]
4. Tikadzumi S. Fizika ferromagnetizma. Magnitnye kharakteristiki i ikh primeneniya [Physics of ferromagnetism. Magnetic characteristics and their applications]. - M.: Mir, 1987. - 420 p. [in Russian]
5. Bessonov L.A. Teoreticheskie osnovy elektrotekhniki [Theoretical foundations of electrical engineering]. - M.: Vysshaya shkola, 1964. - 750 p. [in Russian]
6. Arutyunov Yu.A. Vliyanie topologii magnitoprovoda na otklik pri vneshnem elektromagnitnom vozdeystvii / Yu.A. Arutyunov, A.A. Drobyazko, A.I. Krylov, Ye. A. Chaschin, P.A. Shashok, I.V. Shilov // Sovremennye naukoemkie tekhnologii [Modern high technologies].- 2016.- №10.- P. 29-32. [in Russian]
7. Arutyunov Yu.A. Sravnitel'nyy analiz vliyaniya topologii magnitoprovoda na otklik pri vneshnem elektromagnitnom vozdeystvii dlya magnitoprovoda s razlichnymi geometricheskimi parametrami [Сomparative analysis of the impact of topology on magnetic response when an external electromagnetic action to the magnetic circuit with different geometric parameters] [Electronic resource] / Yu.A. Arutyunov, A.A. Drobyazko, A.I. Krylov, Ye. A. Chaschin, P.A. Shashok, A.A. Mitrofanov // Internet-zhurnal «NAUKOVEDENIE» [Internet journal "Scientometrics"]. – 2017.- Vol. 9.- №1 http: // naukovedenie.ru/PDF/23TVN117.pdf (dostup svobodnyy). Zagl. s ekrana. Yaz. rus., angl. [in Russian]
8. Arutyunov Yu.A. Vliyanie topologii Mebiusa na magnitnye svoystva magnito-myagkikh ferromagnetikov v zamknutoy magnitnoy tsepi [The influence of the mobius topology on the magnetic properties of magnetically soft ferromagnetic materials in a closed magnetic circuit] [Electronic resource] / Yu.A. Arutyunov, N.P. Badalyan, A.A. Drobyazko, Ye. A. Chaschin, P.A. Shashok // Internet-zhurnal «NAUKOVEDENIE» [Internet journal "Scientometrics"]. – 2017.- Vol. 9.- №1 http: // naukovedenie.ru/PDF/53TVN117.pdf (dostup svobodnyy). Zagl. s ekrana. Yaz. rus., angl. [in Russian]
9. Arutyunov Yu.A. Vliyanie topologii lista Mebiusa na magnitnye kharakteristiki polya vne magnitoprovoda [The effect of topology of the mobius strip on the magnetic characteristics of the field outside the magnetic circuit] / Yu.A. Arutyunov, I.N. Vozovikov, A.A. Mitrofanov, Ye. A. Chaschin, L.I.Shemanaeva, S.N. Zhivaev // Sovremennye naukoemkie tekhnologii [Modern high technologies].- 2016.- №7, P. 9-14. [in Russian]
10. Evstigneev N.M. Nekotorye sootnosheniya na provodnike v vide lista Mebiusa [Some of the ratio on the conductor in the form of a Mobius strip] / N.M. Evstigneev, O.I. Ryabkov, I.M. Shakhparonov, S.I. Lavrov // Estestvennye i tekhnicheskie nauki [Natural and technical Sciences].- 2011.- №9.- P. 50-58. [in Russian]
11. Men'shikh O.F. Sposob kosokrugovogo namagnichivaniya ferromagnitnogo toroida [Method kosorukova of magnetization of the ferromagnetic toroid], Patent RF №2391730, opubl. v byull. №16 ot 10.06.2010. [in Russian]
12. Men'shikh O.F. Sposob polucheniya energii i ustroystvo dlya ego realizatsii [The method of obtaining energy and device for its implementation] , Patent RF №2332778, opubl. v byull. №24 ot 17.08.2008. [in Russian]
13. Nalimov V.V. Teoriya eksperimenta [The theory of the experiment].- M.: Nauka, 1971. – 208 p. [in Russian]
14. Vonsovskiy S.V. Magnetizm. Magnitnye svoystva dia-, para-, ferro-, antiferro-, i ferrimagnetikov [Magnetism. Magnetic properties of dia-, para-, ferro-, antiferro-, and ferrimagnetic materials]. - M.: Nauka, 1971. - 805 p. [in Russian]
15. Harrison R. G. Variable-domain-size theory of spin ferromagnetism // IEEE Trans. Magn. 2004. Vol. 40. № 3. P. 1506-1515.