ОБ УДВОЕНИИ ЧАСТОТЫ ЗВУКОВЫХ КОЛЕБАНИЙ В ВИХРЕВОМ ЭЖЕКТОРЕ

Сергеев М.Н.

ORCID: 0000-0002-3428-0288, Кандидат технических наук, Рыбинский государственный авиационный технический университет имени П.А. Соловьева

ОБ УДВОЕНИИ ЧАСТОТЫ ЗВУКОВЫХ КОЛЕБАНИЙ В ВИХРЕВОМ ЭЖЕКТОРЕ

Аннотация

В работе рассмотрена проблема  удвоения частоты звукового излучения, возникающего при работе прямоточного вихревого эжектора. Предлагается объяснение данного явления, согласно которому при распаде вихревого ядра  возникают два спиральных вихря, расположенных диаметрально противоположно друг другу.  Вихри совершают регулярное прецессионное вращательное движение и тем самым вызывают звукоизлучение удвоенной частоты. Приводятся также уточненные выражения для расчета частоты звука в зависимости от геометрических и режимных параметров работы эжектора.

Ключевые слова: звук, вихревой эжектор, прецессия, вихревое ядро, частота.

Sergeev M.N.

ORCID: 0000-0002-3428-0288, PhD in Engineering, Rybinsk State Aviation Technical University named after P.A. Solovyov

ON SOUND VIBRATION FREQUENCY DOUBLING IN SWIRLING EJECTOR

Abstract

The problem of doubling the frequency of sound radiation arising during the operation of a direct-flow swirling ejector pump is considered in the paper. The explanation of this phenomenon is proposed. According to it, the decomposition of the swirling core cause the rise of a swirling ejector pump, located diametrically opposite to each other. Swirling ejector pumps perform a regular precessional rotational motion and thereby cause a doubled frequency sound. Accurate expressions for the calculation of the sound frequency are given, depending on the geometric and operating parameters of the ejector.

Keywords: sound, swirling ejector pump, precession, swirling core, frequency.

Работа вихревых устройств, получивших широкое распространение в различных отраслях промышленности, сопровождается интенсивной генерацией звука [1, с. 1]. Особенно сильно это явление проявляется в вихревых эжекторах прямоточного типа (рис. 2). Это связано с тем, что конструкция такого устройства очень похожа на конструкцию вихревого генератора звука (рис. 2) [2, с. 777]. Действительно, и в той и в другой конструкциях присутствуют вихревая камера и следующее за ней расширение в окружающую среду. В случае эжектора оно обычно ограничивается диффузором.

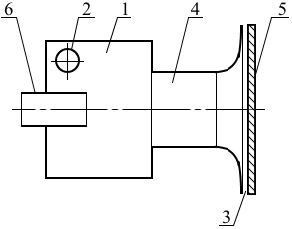
Рис. 1 – Схема конструкции прямоточного вихревого эжектора: 1 – вихревая камера; 2 – тангенциальный ввод; 3 –область расширения; 4 – камера смешения; 5 – диффузор, 6 – патрубок пассивного потока

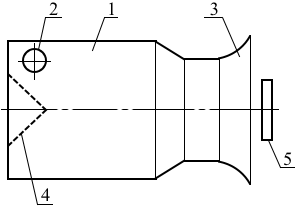
Рис. 2 – Схема конструкции вихревого генератора звука: 1 – вихревая камера; 2 – тангенциальный ввод; 3 –область расширения; 4 – конусная вставка; 5 – турболизатор

 

На рис. 2 показана простейшая конструкция вихревого генератора звука. Более сложные варианты, и в тоже время более эффективные по звукоизлучению, содержат дополнительные элементы. Так на торцевой стенке со стороны завихрителя устанавливают конусную вставку 4, которая способствует формированию приосевого вихря. Со стороны выхода из устройства может быть установлен турбулизатор 5 поступающего из атмосферы воздуха, что приводит к более активному взаимодействию потоков в области зоны рециркуляции.

Причиной возникновения акустических колебаний в вихревых генераторах звука считается прецессионное движение вихревого ядра закрученного потока [3, с. 9]. Схема такого движения показана на рис. 3 [4, с.159].

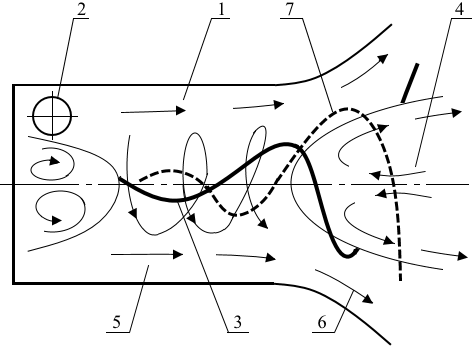
Рис. 3 – Схема течения газа в вихревом генераторе звука: 1 – вихревая камера; 2 – тангенциальный ввод; 3 – вихревое ядро; 4 – зона рециркуляции; 5 – периферийный вихрь; 6 – область расширения; 7 –дополнительная вихревая структура

 

Механизм звукообразования можно описать следующим образом. Газ поступает в вихревую камеру 1 через тангенциальный ввод 2, с помощью которого получает закрутку. В приосевой области при этом формируется вихревое ядро 3. Вследствие закрутки давление на оси вихревого устройства падает и в эту область устремляются массы газа из окружающей среды. Возникает обратный ток или зона рециркуляции 4. Вихревое ядро 3, двигаясь навстречу к зоне рециркуляции, взаимодействует с ней, испытывает торможение и в результате смещается относительно оси, совершая вокруг нее вращательное движение [4, с.158].

При этом создаются периодические пульсации давления, которые и распространяются далее в виде звуковых волн. Возникающее таким образом движение называют прецессионным, потому что его физическая природа связана с гироскопическим эффектом, аналогичным прецессионному движению волчка. Вынуждающий такое движение момент сил связывают при этом с аэродинамической силой, возникающей при обтекании вращающимся потоком смещенного вихревого ядра (эффект Магнуса).

В работе [5, с. 201–203] изучались подобные колебания, возникающие непосредственно в вихревом эжекторе. Особенностью полученных результатов является то, что при переходе через определенное значение давления воздуха на входе в эжектор главная мода акустических колебаний испытывает скачек по частоте ровно в два раза (рис. 4).

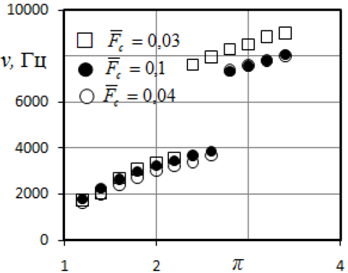
Рис. 4 – Результаты исследования акустических характеристик работы вихревого эжектора

Объяснить данное явление можно следующим образом. При взаимодействии с возвратным течением приосевой вихрь или ядро теряет устойчивость, но при этом оно может и не отклоняется от оси вращения, а пойти по пути развала на два спиральных вихря, расположенных диаметрально противоположно друг другу (рис. 3).

Далее эти вихри совершают регулярное прецессионное вращательное движение, периодически деформируя периферийный закрученный поток и тем самым вызывая звукоизлучение удвоенной частоты. Двойной распад приосевого вихря наблюдался экспериментально [6, с. 117]. На рис.5 представлено схематическое изображение результата опытов по визуализации потока вращающейся жидкости с такого рода распадом.

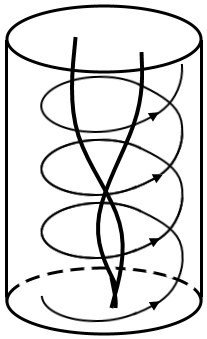
Рис. 5 – Распад вихревого ядра на две вихревые нити

 

Анализ экспериментальных данных, проведенный в работе [5, с. 202] позволил получить эмпирическое соотношение для частоты возникающих в вихревом эжекторе колебаний, в виде критериального уравнения:

  (1)

где   – число Струхаля, рассчитанное по скорости потока u в сопловом вводе, диаметру вихревой камеры D и частоте звука ν; М = u/c – число Маха на входе в сопловой ввод, с – скорость звука,  π = P/P_a – перепад давления на входе в эжектор по отношению к давлению атмосферы.

По всей видимости, формула вида (1) является обоснованной для прямоструйных излучателей, где частота звука напрямую зависит от скорости истечения струи и, как следствие, пропорциональна значению величины .

В вихревых же устройствах существенную роль играет величина зона рециркуляции и поток газа, определяемый степенью разряжения на оси вихря, что в формуле (1) ни как не учитывается. Главным недостатком формулы (1) является также и то, что она не отражает влияния геометрических параметров конструкции эжектора на частоту звука.

Основным геометрическим параметром вихревого эжектора является площадь сечения соплового ввода F_c. Другие геометрические характеристики эжектора, к которым относится  диаметр вихревой камеры D, диаметр камеры смешения d, а также длины этих камер L и s соответственно, практически всегда выбираются из условия D/d = 2, L/D = s/d = 1. Стоит отметить, что с точки зрения теории подобия и размерностей также не вполне корректно выражать один определяемый параметр – число Струхаля Sh – через другой  определяемый параметр – число Маха М.

Таким образом, система безразмерных величин определяющих процесс прецессионных колебаний должна включать в себя безразмерную частоту , перепад давления π, и площадь безразмерную соплового ввода, отнесенную к площади сечения вихревой камеры, f_c = F_c/(πD²/4).

В результате искомое критериальное уравнение примет вид:

  (2)

Используя метод наименьших квадратов и данные, приведенные в работе [5, c. 202], получаем следующие значения искомых коэффициентов: a = 0,35; b = 0,034; c =0,4 для диапазона давлений до скачка частоты и, соответственно, a = 0,62; b = 0,077; c =0,32 после скачка частоты.

Полученное уравнение (2) согласуется с экспериментальными данными с погрешностью не превышающей 2%. Пределы применимости критериального уравнения (2) соответствуют 0,03 < f_c < 0,1; 1,2 < π <3,5, переход на удвоенную частоту происходит при π = 2,4 – 2,6.

Как видно из полученных данных влияние f_c на частоту звука после скачка частоты существенно возрастает, в то время как при малых перепадах давления этим влиянием вообще можно пренебречь.

В заключение следует отметить, что для того, чтобы однозначно установить причину удвоения частоты колебаний в вихревом прямоточном эжекторе и доказать её связь с прецессионными колебаниями вихревого ядра, необходимо провести детальное экспериментальное исследование структуры закрученного потока. Так, например, при установке акустических датчиков в диаметрально противоположных точках вихревой камеры при распаде вихревого ядра на две вихревые нити следует ожидать поступление от датчиков сигнала в фазе, а при одиночном вихре будет иметь место корреляция сигналов в противофазе. Изучение данного явления помимо научного интереса важно также и с практической точки зрения, так как оно напрямую связано с разработкой и производством работающих на этом принципе счетчиков расхода и вихревых сирен.

Список литературы / References

1. Кныш Ю.А. Автоколебания в закрученных струях. – Самара: Изд-во Самарского научного центра РАН, 2006. – 248 с.
2. Кныш Ю.А. Лукачев С.В. Экспериментальное исследование вихревого генератора звука // Акустический журнал. – 1977. – Т.23, №5. – С. 776–782.
3. Киясбейли А.Ш., Перельштейн М.Е. Вихревые измерительные приборы. – М.: «Машиностроение», 1978. – 152 с.
4. Вихревой эффект и его применение в технике. // Материалы 5 Всесоюзной научно-технической конференции. – Куйбышев: КуАИ, 1988. – 248 с.
5. Иванов Р. И., Пиралишвили Ш. А., Сергеев М. Н. Экспериментальное исследование акустических колебаний в вихревом эжекторе // Вестник РГАТУ имени П.А. Соловьева. – 2011. – №2(20). – С. 201–204.
6. Алексеенко С.В., Окулов В.Л. Закрученные потоки в технических приложениях // ТИА. – 1996.– Т.3, №2. – С. 101–137.

Список литературы на английском языке / References in English

1. Knysh Yu.A. Avtokolebaniya v zakruchennyh struyah [Self-oscillations in the twirled streams]. – Samara: Izd-vo Samarskogo nauchnogo centra RAN [Samara scientific center of RAS], 2006. – 248 P. [in Russian]
2. Knysh Yu.A. Lukachev S.V. Eхsperimental'noe issledovanie vihrevogo generatora zvuka [The experimental study of the vortex generator of a sound]// Akusticheskij zhurnal. – 1977. – T.23, №5. – Р. 776–782. [in Russian]
3. Kiyasbejli A.SH., Perel'shtejn M.E. Vihrevye izmeritel'nye pribory. [Vortex measuring apparatuses] – M.: «Mashinostroenie», 1978. – 152 Р. [in Russian]
4. Vihrevoj ehffekt i ego primenenie v tekhnike [Vortex effect and its application in technique] // Materialy 5 Vsesoyuznoj nauchno-tekhnicheskoj konferencii.[Proceedings of the fifth All-Union scientific and technical conference] – Kujbyshev: KuAI, 1988. – 248 Р. [in Russian]
5. Ivanov R. I., Piralishvili SH. A., Sergeev M. N. Eхsperimental'noe issledovanie akusticheskih kolebanij v vihrevom ehzhektore [Рilot study of acoustic oscillations in a vortical ejector] // Vestnik RGATU imeni P.A. Solov'eva [The P. A. Solovyov RGATU bulletin]. – 2011. – №2(20). – Р. 201–204. [in Russian]
6. Alekseenko S.V., Okulov V.L. Zakruchennye potoki v tekhnicheskih prilozheniyah [The twirled streams in technical appendices]// TIA. – 1996.– V.3, №2. – Р. 101–137. [in Russian]