ИССЛЕДОВАНИЕ НАПРЯЖЁННО-ДЕФОРМИРОВАННОГО СОСТОЯНИЯ УПЛОТНИТЕЛЯ ПОРШНЯ И СИСТЕМЫ «УПЛОТНИТЕЛЬ-ЦИЛИНДР»

Душко О.В.¹, Воронкова Г.В.², Рекунов С.С.³

¹Кандидат технических наук, доцент, Волгоградский государственный технический университет,

²ORCID: 0000-0001-5837-3895, Кандидат технических наук, доцент, Волгоградский государственный технический университет,

³ORCID: 0000-0002-9360-8239, Кандидат технических наук, доцент, Волгоградский государственный технический университет,

ИССЛЕДОВАНИЕ НАПРЯЖЁННО-ДЕФОРМИРОВАННОГО СОСТОЯНИЯ УПЛОТНИТЕЛЯ ПОРШНЯ И СИСТЕМЫ «УПЛОТНИТЕЛЬ-ЦИЛИНДР»

Аннотация

Рассмотрена задача по оптимизации геометрических размеров уплотнителя поршня с применением метода генетического алгоритма, позволяющая равномерно распределить по внешней поверхности уплотнителя силы трения, возникающие при работе механизма. Предложена методика исследования напряжённо-деформированного состояния уплотнителей поршней с введением функции напряжений в геометрические и физические уравнения классической линейной теории упругости. Сравнение результатов показало, что аппроксимация изменения модуля упругости от толщины модифицированного слоя совпадает с экспериментальными значениями.

Ключевые слова: уплотнитель, напряжение, оптимизация, генетический алгоритм.

Dushko O.V.¹, Voronkova G.V.², Rekunov S.S.³

¹PhD in Engineering, Associate Professor, Volgograd State Technical University,

²ORCID: 0000-0001-5837-3895, PhD in Engineering, Associate Professor, Volgograd State Technical University,

³ORCID: 0000-0002-9360-8239, PhD in Engineering, Associate Professor, Volgograd State Technical University

INVESTIGATION OF THE STRESS-STRAIN DEFORMATION OF THE PISTON SEAL AND SEALER-CYLINDER SYSTEM

Abstract

The geometric dimensions optimization problem of the piston sealant with the genetic algorithm method is considered in the paper. The method makes it possible to distribute frictional forces along the outer surface of the sealant, which arise during the operation of the mechanism. The authors proposed a technique for studying the stress-strain deformation of piston sealers with the introduction of the stress function into the geometric and physical equations of the classical linear theory of elasticity. The comparison of the results showed that the approximation of the change in the modulus of elasticity from the thickness of the modified layer coincides with the experimental values.

Keywords: sealer, strain, optimization, genetic algorithm.

Надёжность и безопасность производственных объектов в машиностроении и нефтехимии зависит от совершенства и долговечности объёмных гидроагрегатов возвратно-поступательного действия, в которых уплотнители являются наиболее уязвимым местом, особенно в их опорной части. В данной работе исследуется напряжённо-деформированное состояния уплотнителя и системы «уплотнитель-цилиндр» для заданных произвольной начальной геометрии уплотнителя и рабочего давления жидкости, а также предложена методика определения оптимальных геометрических параметров уплотнителя.

Уплотнитель находится в осесимметричном относительно оси z напряжённом состоянии. При этом напряжения и деформации изменяются только вдоль двух координатных осей z и r (уплотнитель рассматривается в разрезе) (рис. 1). Деформации уплотнителя малы (ε < 10 %), вследствие этого связь между напряжениями и деформациями может быть описана линейной зависимостью (закон Гука).

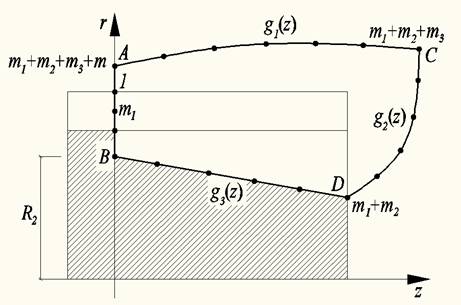
Рис. 1 -  Начальная геометрия манжеты  в свободном состоянии

Для определения напряжённо-деформированного состояния уплотнителя используются уравнения теории упругости, связывающие между собой линейные и угловые перемещения с модулем упругости. При определённой интерпретации применительно к уплотнителю поршня, для осесимметричной задачи согласно [1] имеем:

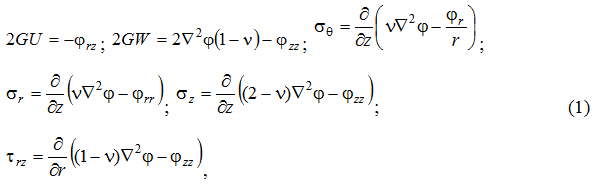
где φ  – неизвестная функция перемещений; υ – коэффициент Пуассона;  – модуль сдвига; Е – модуль упругости; U, W – линейные перемещения в направлении соответственно осей r и z;  – нормальные напряжения соответственно кольцевые, радиальные и направленные вдоль оси z (все напряжения сжатия); τ – касательное напряжение.

Функции перемещений и оператор Лапласа

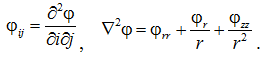                                                  (2)

Для повышения устойчивости вычислительного процесса и точности вычислений вводятся безразмерные параметры:

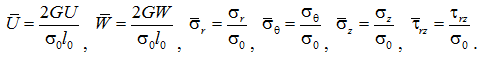                  (3)

где σ₀ – напряжение, численно равное модулю упругости материала; l₀ – линейный размер, имеющий порядок размера исследуемой области.

Функция напряжений по [1] является решением уравнения

                                                                                     (4)

и при этом должны выполняться граничные условия.

Для решения поставленной задачи и введённых безразмерных параметров (3) принята следующая функция напряжений:

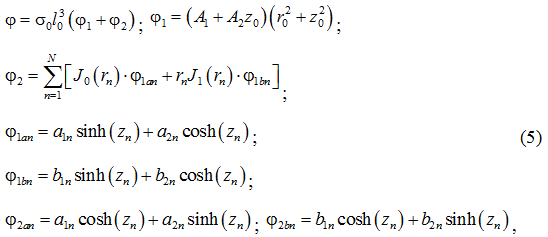
где А₁, А₂, а_i, b_i – постоянные коэффициенты, определяемые из граничных условий;

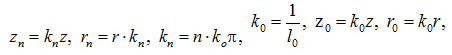                (6)

где r, z – текущие координаты; J_n – функция Бесселя 1-го рода n-го порядка.

Принятая функция напряжений (5) является решением уравнения (4). Для решения поставленной задачи необходимо определение постоянных коэффициентов для удовлетворения граничных условий.

Функция (5) позволяет полностью описать напряжённо-деформированное состояние уплотнителя. Использование в уравнениях (5) функции Бесселя 1-го рода объясняется особенностями решения данной осесимметричной задачи (применительно к резиноёмкому уплотнителю поршня). Как известно, функция Бесселя 1-го рода является убывающей (в данном случае по координате r), что обеспечивает получение устойчивого вычислительного процесса.

Подстановка функции (5) в исходные уравнения (1), с учётом введённых безразмерных параметров (3), приводит к следующим выражениям для напряжений и перемещений:

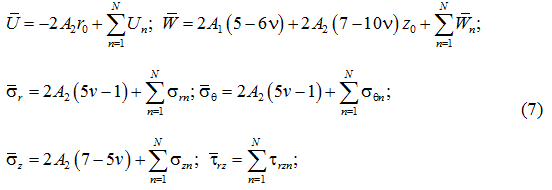
где

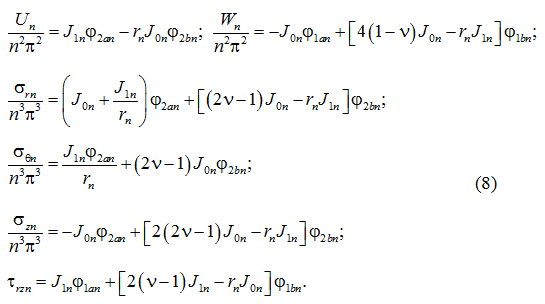
Решение (7) и (8) должно удовлетворять граничным условиям на контуре. Для геометрии исследуемой области и нагрузок эти граничные условия будут следующими [2]:

Участок АВ (свободный контур):                          (9)

Участок ВС (нет перемещений):                               (10)

Участок СD (давление р жидкости):

                                                  (11)

где l, m – направляющие косинусы (рис. 2.7, а)   – уравнение контура СD.

Участок DА (контакт с цилиндром):                                      (12)

где  f – коэффициент трения;

Вторым граничным условием являются деформации вдоль оси r – от  до , а с учётом безразмерных параметров:

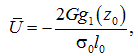                                                                              (13)

где  – уравнение контура в недеформированном состоянии.

Неизвестные коэффициенты функции напряжений (5) определяются из решения системы линейных алгебраических уравнений. Граничные условия (9) - (13) удовлетворяются на каждом контуре приближённо. Их точное соответствие выполняется лишь в отдельных точках контура, число которых может быть произвольным. Увеличение числа этих точек приводит к повышению точности решения задачи; расстановка точек показана на рис.1.

Количество неизвестных коэффициентов в (5) и порядок системы уравнений равен удвоенному числу точек контура. Полученное решение достаточно точно удовлетворяет всем уравнениям теории упругости при приближённом выполнении граничных условий.

В области контакта на границе DA, в случае модифицирования уплотнителя, модуль упругости материала изменяется вдоль координаты r – на толщине t – от значения Е₁ на поверхности до значения Е упругого тела [3]. Это изменение аппроксимируется следующей зависимостью:

                                                                                     (14)

где 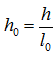 – расстояние от поверхности тела.

Выражение (14) хорошо описывает изменение модуля упругости от толщины модифицированного слоя, определённое экспериментально [4]. При этом коэффициент α в (14) определяется по значению толщины t слоя:

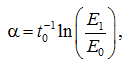                                                                               (15)

где 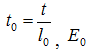  – модуль упругости основного объёма (в сердцевине уплотнителя).

Влияние модифицированного слоя на поведение исследуемой области учитывается приближённо – введением дополнительной пограничной области D^*A^* с приведённым модулем упругости Е^*. Эта область соприкасается со стороной DA. Касательные напряжения по контакту границ DA и D^*A^* вызывают изменение перемещений точек границы DA, что влияет на напряжения и деформации всей исследуемой области. Контактные касательные напряжения τ^* представлены степенным рядом через неизвестные коэффициенты :

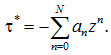                                                                                  (16)

При этом из уравнения равновесия для слоя D^*A^*

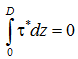
определяется коэффициент  ряда (16)

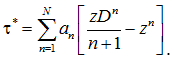                                                                     (17)

Нормальные напряжения в области D^*A^* принимаются равномерно распределёнными по её толщине t и определяется из условия равновесия:

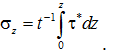                                                                                  (18)

Перемещения W^* слоя D^*A^* определяется по закону Гука:

                                                                   (19)

где  – приведённый модуль упругости; С – постоянный коэффициент.

При этом

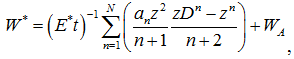                                              (20)

где  – перемещение точки А границы.

Введение модифицированного слоя изменяет граничное условие (12) для касательных напряжений. На границе DA

                                                                                    (21)

где  – определяется из (17).

Коэффициенты ряда (17) находят из условия совместимости перемещений соответственно границы DA и модифицированного слоя D^*A^* в N точках контакта:

                                                                                          (22)

Модуль упругости дополнительной пограничной области D^*A^* изменяется в соответствии с (14) от  до  на глубину :

                                                                              (23)

Приведённый модуль упругости Е^* определяется из условия равенства продольных сил в дополнительном слое с переменным модулем упругости (23) и постоянным Е^*:

                                                                     (24)

где А – площадь сечения дополнительного слоя.

Подстановка (23) в (24) определяет приведённый модуль упругости:

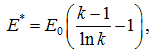                                                                          (25)

где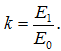 

С целью определения оптимальной геометрии уплотнителя будем использовать метод генетических (эволюционных) алгоритмов [5]. Этот метод используется для решения задач моделирования и оптимизации решений путем случайного подбора, вариации и комбинирования большого количества исходных параметров или когда невозможно предсказать область нахождения оптимального решения.

Применительно к уплотнителям резинометаллических поршней метод генетических алгоритмов использовался для поиска оптимальной конфигурации зоны контакта уплотнителя (область DA). При этом функция , выражающая форму поверхности контакта, имеет следующий вид:

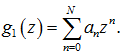                                                                               (26)

Коэффициенты  ряда (26) определяются в процессе эволюции, при этом N – число членов ряда аппроксимирующей функции; z – текущая координата на поверхности уплотнителя.

Функция цели определяет соответствие решения оптимальному и принята в виде взвешенной комбинации решений:

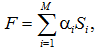                                                                                    (27)

где α_i – весовые коэффициенты (вклад, учитываемый в стадии стирания на  значение функции цели); S_i – сумма квадратов отклонений контактного напряжения σ_z от среднего; М – количество слоёв стирания (износа) материала уплотнителя.

Функция цели (27) даёт возможность определить оптимальную конфигурацию уплотнителя для максимально равномерного распределения контактных напряжений в процессе работы и стирания материала.

Список литературы / References

1. Ильин В. П. Численные методы решения задач строительной механики / В. П. Ильин, В. В. Карпов, A. M. Масленников. – Минск: Вышэйшая школа, 1990. –349 с.
2. Самарский А. А. Методы решения сеточных уравнений / А. А. Самарский, Е. С. Николаев. – Москва: Наука, 1978. – 592 с.
3. Тимошенко С. П. Пластинки и оболочки / С. П. Тимошенко, С. Войновский-Кригер. – Москва: Физматгиз, 1963. – 636 с.
4. Трушин С.И. Расчет пластин и пологих оболочек методами нелинейного программирования / С. И. Трушин // Вестник Российского университета дружбы народов. Серия: Инженерные исследования. – 2003. – № 2. – С. 40-45.
5. Родин С. И. Эволюционные методы для создания оптимальных пространственных стержневых систем / Г. И. Беликов, С. И. Родин // Сборник научных статей. Российская академия архитектуры и строительных наук, Южное региональное отделение РААСН, Администрация Волгоградской области, Волгоградский государственный архитектурно-строительный университет. Волгоград. – 2010. – С. 79-82.

Список литературы на английском языке / References in English

1. Il’in V. P. Chislennye metody resheniya zadach stroitelnoy mehaniki [Numerical methods for solving problems of structural mechanics] / V. P. Il’in, V. V. Karpov, A. M. Maslennikov. Minsk, 1990. – 349 p. [in Russian]
2. Samarskiy A. A. Metody resheniya setochnyh uravneniy [Methods of solving the mesh equations] / A. A. Samarskiy, E. S. Nikolaev. Moscow, 1978. – 592 p. [in Russian]
3. Timoshenko S. P. Plastinki i obolochki [Plates and shells] / S. P. Timoshenko, S. Voynovskiy-Kriger, Moscow, 1963. – 636 p. [in Russian]
4. Trushin S. I. Raschyot plastin i pologih obolochek metodami nelineynogo programmirovaniya [Calculation of plates and shallow shells by methods of nonlinear programming] / S. I. Trushin // Vestnik Rossiyskogo universiteta druzhby narodov. Seriya: Inzhenernye issledovaniya [Bulletin of the RUDN University. Series 3. Physics. Astronomy]. – 2003. – № 2. – P. 40-45. [in Russian]
5. Rodin S. I. Jevoljucionnye metody dlja sozdanija optimal'nyh prostranstvennyh sterzhnevyh sistem [Evolutionary methods for creating optimal spatial rod systems] / G. I. Belikov, S. I. Rodin // Sbornik nauchnyh statej. Rossijskaja akademija arhitektury i stroitel'nyh nauk, Juzhnoe regional'noe otdelenie RAASN, Administracija Volgogradskoj oblasti, Volgogradskij gosudarstvennyj arhitekturno-stroitel'nyj universitet. Volgograd [Collection of scientific articles. Russian Academy of architecture and construction Sciences, southern regional office RAASN, the Volgograd region Administration, Volgograd State University of Architecture and Civil Engineering. Volgograd]. – 2010. P. 79–82. [in Russian]