АПРОБАЦИЯ МЕТОДИКИ ДОЛГОСРОЧНОГО ПРОГНОЗИРОВАНИЯ СТАТИСТИЧЕСКИХ ХАРАКТЕРИСТИК НА РЕЧНЫХ БАССЕЙНАХ ИРАНА

Гайдукова Е.В.¹, Джалалванд А.², Синкпеун Л.³

¹ORCID: 0000-0002-3547-5538, кандидат технических наук, доцент, ²ORCID: 0000-0003-2311-5065, аспирант, ³ORCID: 0000-0001-9297-2904, аспирант, Российский государственный гидрометеорологический университет (РГГМУ)

АПРОБАЦИЯ МЕТОДИКИ ДОЛГОСРОЧНОГО ПРОГНОЗИРОВАНИЯ СТАТИСТИЧЕСКИХ ХАРАКТЕРИСТИК НА РЕЧНЫХ БАССЕЙНАХ ИРАНА 

Аннотация

В статье рассматривается возможность применения методики оценки последствий изменения климата к речным бассейнам Ирана. В качестве исследуемых взяты бассейны рек Сефидруд и Карун. Апробация методики произведена на ретроспективном материале с выделением маловодных и многоводных фаз водности с целью имитации условий изменения климата. В основе прогнозной методики лежит уравнение Фоккера–Планка–Колмогорова. Получено, что для надежных оценок статистических характеристик речного стока рек Ирана необходимо использовать региональные зависимости для параметров прогнозного уравнения.

Ключевые слова: гидрология, прогнозирование, разностно-интегральные кривые, ретроспективные данные, изменение климата.

Gaidukova E. V.¹, Jalalvand A.², Sinkpehoun L.³

¹ORCID: 0000-0002-3547-5538, PhD in Engineering, Associate professor, ²ORCID: 0000-0003-2311-5065, Postgraduate student, ³ORCID: 0000-0001-9297-2904, Postgraduate student, Russian State Hydrometeorological University (RSHU), Saint-Petersburg

APPROBATION OF METHODS OF LONG-TERM FORECASTING OF STATISTICAL CHARACTERISTICS ON RIVER BASINS OF IRAN

Abstract

The article considers the possibility of applying the methodology for assessing consequences of the climate change to the river basins of Iran. The paper investigates Sefīd-Rūd and Kārun river basins. Approbation of the technique was performed with the help of retrospective material with the identification of low-water and high-water content phases with the aim of simulating climate change conditions. The forecast method is based on the Fokker-Planck-Kolmogorov equation. According to the results, reliable estimates of statistical characteristics of the river flow in Iran, it is necessary to use regional dependencies for the parameters of the forecast equation.

Keywords: hydrology, forecasting, difference integral curves, retrospective data, climate change.

Введение

В настоящее время факт изменения климата подтверждается инструментальными данными [1]. Возникает задача оценки последствий изменения климата на различные отрасли экономики. Существует несколько подходов в этом направлении (см. например, [2, 3, 4, 5]), в том числе методика, разработанная в Российском государственном гидрометеорологическом университете (РГГМУ) [6].

Целью данного исследования является апробация методики РГГМУ на речных бассейнах Ирана на ретроспективном материале, т. е. составление поверочных прогнозов статистических характеристик речного стока.

Исходные данные

В качестве исследуемых речных бассейнов были взяты водосборы рек Сефидруд и Карун, которые располагаются на севере и юго-западе Ирана. Расположение гидрологических постов в бассейнах Сефидруд и Карун представлено на рис. 1. Были отобраны посты с незарегулированным стоком и замыкающие зональные площади водосборов. Всего получилось 28 постов из 56 имеющихся. Продолжительность рядов составляет в среднем 39 лет, большинство рядов начинаются с 1968 года и заканчиваются 2006 годом.

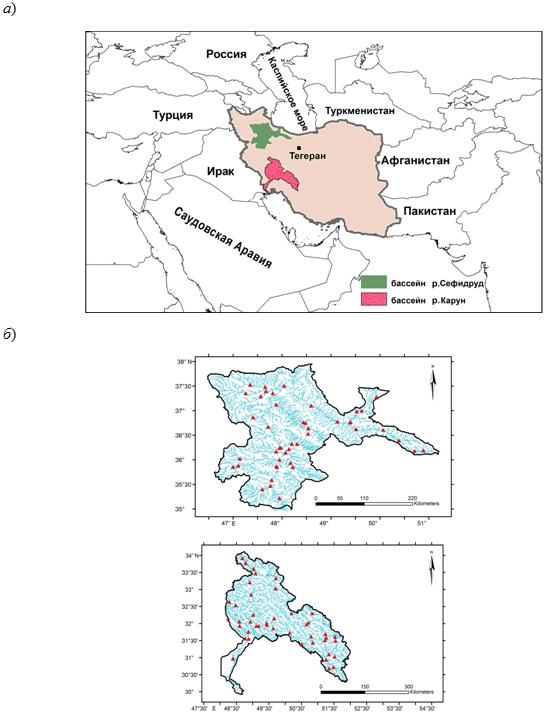
Рис. 1 – Местоположение речных бассейнов Сефидруд и Карун (а) и гидрологических постов (б)

 

Методика ретроспективных прогнозов

В основе методики РГГМУ лежит уравнение Фоккера–Планка–Колмогорова (ФПК), которым описывают эволюцию плотности вероятности марковских случайных процессов. Частным случаем уравнения ФПК для стационарных случайных процессов является уравнение Пирсона:

  (1)

где p – плотность вероятности; Q – характеристика речного стока; a, b₀, b₁, b₂ – постоянные коэффициенты.

Решением уравнения (1) является семейство кривых плотности вероятности Пирсона, используемые в инженерной гидрологии. Так как к уравнению Пирсона переходим от ФПК, то коэффициенты приобретают физический смысл, связываясь со свойствами подстилающей поверхности и внешними климатическими факторами. Следовательно, наличие сценарных оценок климатических элементов позволяет оценить возможное сценарное распределение стока.

С учетом того, что климатические сценарии имеют квазистационарный характер (т. е. без изменений за данный интервал времени, за который заданы сценарные оценки метеоэлементов) для практического применения уравнение ФПК можно аппроксимировать системой уравнений для начальных статистических моментов :

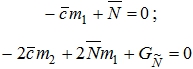  (2)

где  – коэффициент стока; τ – время релаксации речного бассейна (для многолетнего стока τ = 1 год);  – интенсивность климатического шума;  – интенсивность осадков; m₁, m₂ – первый и второй момент соответственно.

Данная система упрощена от первоначального варианта по следующим соображениям [6]: 1) не учитывается коэффициент эксцесса из-за небольшой продолжительности рядов, приводящей к большим погрешностям при построении вероятностного распределения стоковых характеристик; 2) для коэффициента асимметрии Cs используется его районное соотношение с коэффициентом вариации Cv; 3) ликвидируются внутренние и взаимные шумы системы для получения устойчивых решений в текущем и в ожидаемом климате; 4) интенсивность климатического шума  принимается постоянной при изменении климата.

Перед использованием системы уравнений (2) для сценарной оценки вероятностных распределений многолетнего годового стока Ирана, необходимо проверить выполнения допустимых условий ее применимости и обосновать справедливость расчетов будущих состояний исследуемого процесса по рассматриваемой методике. Эти анализы можно сделать на основе имеющихся ретроспективных рядах наблюдений.

Алгоритм ретроспективных прогнозов характеристик стока содержит следующие этапы.

1) Разделение ряда расходов воды на части максимально неоднородные друг к другу. Для этого были построены разностно-интегральные кривые, которые показали, что все ряды имеют маловодный и многоводный периоды. На рис. 2 представлен алгоритм выбора года максимального расхождения однородности по среднему. Необходимо было найти год, делящий ряд наблюдений на два периода, разница по среднему между которыми максимальная. По описанному алгоритму были определены года максимального расхождения однородности по среднему для 5 % у. з.

2) Параметризация и прогноз. По данным о средних значениях стока и осадков одной части рассчитываются начальные моменты m₁, m₂ и коэффициенты вариации и стока. Зная коэффициент стока, определяется параметр . Далее обратным решением системы (2) находится величина интенсивности климатического шума . На этом заканчивается этап параметризации модели.

Далее, зная , параметр  и норму осадков за вторую часть ряда, определяются прогнозные значения моментов m_i путем решения системы (2). От моментов переходим к прогнозным значениям статистических характеристик (норма, Cv и Cs). Коэффициент асимметрии определяется по соотношению Cs/Cv,  коэффициент вариации по формуле .

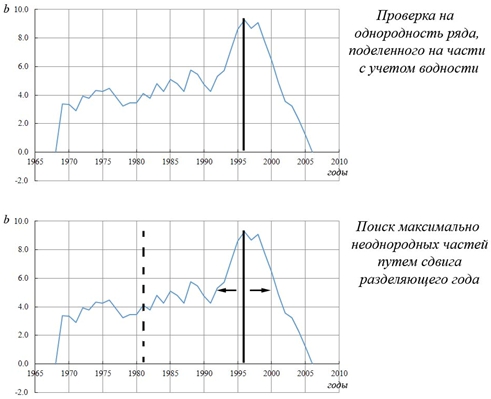
Рис. 2 – Алгоритм разделения рядов стока на две части (b =∑(K_i –1)/Cv, где K_i – модульный коэффициент)

 

Осуществлялись прямые (параметризация производилась по первой части ряда, а прогноз давался на вторую часть) и обратные (параметризация производилась по второй части ряда, и прогноз давался на первую часть) прогнозы. При прогнозах коэффициент стока оставлялся постоянным, т. е. рассчитанным по параметризируемой части ряда.

Результаты, полученные по ретроспективным прогнозам (норма, коэффициенты вариации и асимметрии стока), позволяют построить прогнозные кривые обеспеченностей, которые сравнивались с фактическими. Пример таких кривых показан на рис. 3. Большинство прогнозных кривых имеют значимые отклонения от фактических в зоне малых и больших обеспеченностей.

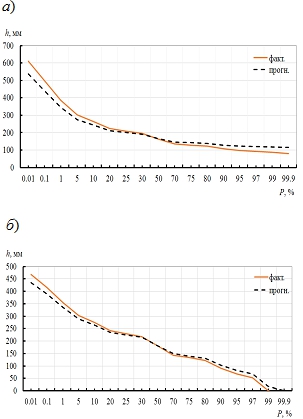
Рис. 3 – Пример фактических и прогнозных кривых обеспеченностей: а – прямой прогноз, б – обратный прогноз (пост Pole Kereh Bast бассейна р. Карун)

Оценка эффективности ретроспективных прогнозов (т. е. проверка соответствия прогнозной кривой фактической) производилась по критерию согласия Пирсона (χ²); результаты показаны в табл. 1 для двух уровней значимости (у.з.).

 

Таблица 1 – Результаты поверочных прогнозов при оценке критерием χ²

Гидрологический пост	Прямой прогноз		Обратный прогноз
	5 % у.з.	10 % у.з.	5 % у.з.	10 % у.з.
Бассейн реки Карун
Patave	+	+	+	+
Kata	–	–	+	+
Pole Kereh Bast	–	–	+	+
Solegan	–	–	+	+
Kohe Sokhte	–	–	+	+
Behesht Abad	–	–	+	+
Barez	+	+	+	+
Arman	+	+	+	+
Rahim Abad	+	+	–	–
Dorud (Tire)	+	+	–	–
Sepid Dashte Sezar	+	+	+	+
Tange Panj-e Sezar	+	+	+	+
Tange Panj	+	+	+	+
Dashte Bozorg	–	–	+	+
Бассейн реки Сефидруд
Bianlod	+	+	–	–
Salalmat Abad	+	+	–	–
Gamishgan	+	+	–	–
Gara goni	+	+	–	–
Yenki Kand	+	+	+	+
Sarcham	+	+	+	+
Pole Dokhtar	+	+	–	–
Igdomosh	–	–	+	+
Octor	+	+	+	+
Nesare Olia	+	+	–	–
Shadi Abad	+	+	–	–
Mah Neshan	+	+	–	–
Myane Sharichai	–	–	+	+
Myane Gharngho	–	–	+	+
Gilavan	+	+	+	+

 

Анализ табл. 1 показал, что при прямом прогнозе оправдалось 20 прогнозов из 28 (для уровней значимости 5 и 10 %), что составляет 71 %. При обратном прогнозе оправдалось 19 прогнозов, что составляет 67 %. В общем получено, что оправдалось 39 прогнозов из 56 – это составляет 69 %. Методика, по которой получены подобные результаты, относится по эффективности прогнозов к категории удовлетворительных. Улучшение результатов прогноза можно получить при использовании локальных зависимостей, например, коэффициента стока с климатическими характеристиками или факторами подстилающей поверхности. Составление подобных зависимостей позволит прогнозировать коэффициент стока в зависимости от климатических и антропогенных сценариев.

Выводы

При прогнозировании статистических характеристик речного стока рек Ирана на ретроспективном материале получены удовлетворительные результаты, которые можно улучшить использованием региональных зависимостей параметров прогнозного уравнения от климатических характеристик.

Список литературы / References

1. Intergovernmental Panel on Climate Change (IPCC) [Электронный ресурс] // IPCC, 2017. – Режим доступа: http://www.ipcc.ch (дата обращения 09.11.2016).
2. Гельфан А. Н. Динамико-стохастическое моделирование формирования стока / А. Н. Гельфан. – М.: Наука, 2007. – 279 с.
3. Георгиевский В. Ю. Гидрологический режим и водные ресурсы / В.Ю. Георгиевский, А. Л. Шалыгин // В кн. Методы оценки последствий изменения климата для физических и биологических систем. – М.: Росгидромет, 2012. – С. 53–86.
4. Добровольский С. Г. Глобальные изменения речного стока / С. Г. Добровольский. – М.: Геос. – 2011. – 659 с.
5. Vinogradov Y. B. An approach to the scaling problem in hydrological modelling: the deterministic modelling hydrological system / Y. B. Vinogradov, O. M. Semenova, T. A. Vinogradova // Hydrological Processes, № 25. – 2011. – P. 1055–1073.
6. Методические рекомендации по оценке обеспеченных расходов проектируемых гидротехнических сооружений при неустановившемся климате / В. В. Коваленко, Н. В. Викторова, Е. В. Гайдукова и др.. – СПб.: изд. РГГМУ. – 2010. – 51 с.

Список литературы на английском языке / References in English

1. Intergovernmental Panel on Climate Change (IPCC) [Electronic resource] // IPCC, 2017. – URL: http://www.ipcc.ch (accessed: 09.11.2016).
2. Gelfan A. N. Dinamiko-stokhasticheskoye modelirovaniye formirovaniya stoka [Dynamic stochastic modeling of flow formation] / A. N. Gelfan. – M., Nauka. 2007. 279 p. [in Russian]
3. Georgiyevskiy V. YU. Gidrologicheskiy rezhim i vodnyye resursy [Hydrological regime and water resources] / V. YU. Georgiyevskiy, A. L. Shalygin // In book Metody otsenki posledstviy izmeneniya klimata dlya fizicheskikh i biologicheskikh sistem [Methods for assessing the effects of climate change on physical and biological systems]. – M., Roshydromet. 2012. – P. 53–86. [in Russian]
4. Dobrovolskiy S. G. Global'nyye izmeneniya rechnogo stoka [Global changes in river flow] / S. G. Dobrovolskiy. – M., Geos. 2011. 659 p. [in Russian]
5. Vinogradov Y. B. An approach to the scaling problem in hydrological modelling: the deterministic modelling hydrological system / Y. B. Vinogradov, O. M. Semenova, T. A. Vinogradova // Hydrological Processes, № 25. – 2011. – P. 1055–1073.
6. Metodicheskiye rekomendatsii po otsenke obespechennykh raskhodov proyektiruyemykh gidrotekhnicheskikh sooruzheniy pri neustanovivshemsya klimate [Methodical recommendations for the assessment of the secured costs of the projected hydraulic structures under unsteady climate] / V. V. Kovalenko, N. V. Viktorova, E. V. Gaidukova et al. – SPb., izd. RSHU, 2010. – 51 p. [in Russian]