ВЛИЯНИЕ МЕТОДОВ ИНТЕРПОЛЯЦИИ ПРОЧНОСТНЫХ СВОЙСТВ ГРУНТОВ НА РЕЗУЛЬТАТЫ РАСЧЕТА УСТОЙЧИВОСТИ СКЛОНОВ

Буфеев Ф.К.¹, Фоменко И.К.², Сироткина О.Н.³

¹Аспирант, Российский Государственный Геологоразведочный Университет им. Серго Орджоникидзе; ²ORCID:0000-0003-23186015, Доктор геолого-минералогических наук, ООО "Научно-производственный центр по инженерным изысканиям"; ³Кандидат геолого-минералогических наук, Московский Государственный Университет им. М.В. Ломоносова

Работа выполнена при поддержке гранта РФФИ №15-05-00577

ВЛИЯНИЕ МЕТОДОВ ИНТЕРПОЛЯЦИИ ПРОЧНОСТНЫХ СВОЙСТВ ГРУНТОВ НА РЕЗУЛЬТАТЫ РАСЧЕТА УСТОЙЧИВОСТИ СКЛОНОВ

Аннотация

В статье выполнено сравнение результатов расчётов устойчивости склонов при использовании различных методов интерполяции свойств грунтов. Рассматриваются четыре метода интерполяции – метод обратно-взвешенных расстояний, метод Чага, метод Делоне и метод сплайна. Анализ оценки устойчивости склона с учетом использования различных моделей интерполяции свойств грунтов показал, что они оказывают влияние на положение расчетной поверхности скольжения и на величину коэффициента устойчивости. Из этого следует, что корректное решение задачи по оценке устойчивости при задании дискретных значений прочностных свойств грунтов должно выполняться с обоснованием используемого метода интерполяции.

Ключевые слова: модели интерполяции свойств грунтов; расчет устойчивости склонов.

Bufeev F.K.¹, Fomenko I.K.², Sirotkina О.N.³

¹Postgraduate student, Russian State Geological Prospecting University n. a. Sergo Ordzhonikidzе; ²ORCID:0000-0003-23186015, PhD in Geology and Mineralogy, Scientific Production Center for Civil Engineering; ³ PhD in Geology and Mineralogy, Moscow State University n. a. M. V. Lomonosov

INFLUENCE OF INTERPOLATION METODS FOR STRENGTH PROPERTIES OF THE SOIL ON THE RESULTS OF CALCULATION OF SLOPE STABILITY

Abstract

In this article a comparison of the results of calculations of slope stability using different interpolation methods of soil properties. We consider four interpolation method - the method of back-weighted distances, Chaga method, Delaunay method and spline method. Analysis of slope stability assessment, taking into account the use of different models of interpolation properties of soils showed that they have an impact on the estimated position of the sliding surface and the value of the stability factor. It follows that the correct solution of the problem to assess the stability of discrete values ​​of strength properties of soils must be carried out with the rationale used by the interpolation method.

Keywords: model interpolation properties of soils; calculation of slope stability.

Введение

Одним из главных этапов выполнения работ по количественной оценке устойчивости склонов является схематизация реального объекта моделирования до геомеханической схемы, используемой при построении математической модели [1]. При этом, наибольшая неопределенность и субъективность связана с  интерпретацией геологического строения и распределением свойств грунтов в склоновом массиве. Следует отметить, что данной проблеме, в отечественном оползневедении уделялось неоправданно мало внимания.

В настоящее время описаны три принципиально отличающиеся схемы возможного распределения свойств грунтов в склоновом массиве [2]:

• Принятый в российской практике подход – в пределах выделенных расчётных геологических элементов (РГЭ) задаются расчётные характеристики свойств грунтов.
• Принятый за рубежом подход – в пределах выделенных РГЭ задаются нормативные характеристики свойств грунтов (например Eurocode 7 - Design approach 1, Combination 1).
• В пределах массива дискретно задаются значения свойств грунтов. В его основе лежит следующая идея: по известным, фактически замеренным величинам свойств грунтов строится поле распределения свойств в массиве.

Отличительной особенностью третьей схемы распределения свойств грунтов является уход от статистической обработки лабораторных данных при построении расчетной модели. Даже самые мелкие геологические тела неоднородны. В отечественной практике неоднородность учитывается за счёт понижения среднего значения характеристики. В зарубежной - используется среднее значение (или математическое ожидание), при этом неоднородность может быть учтена с помощью вероятностных функций распределения физико-механических характеристик грунтов [3, 4, 5, 6]. Минусом традиционных схем является то, что выделяемому в пределах геологического разреза слою назначаются статистически обработанные характеристики, выборка которых включает в себя значения, определённые для этого слоя в других местах. То есть, если выделенный ИГЭ вскрыт в другой скважине, на некотором расстоянии от профиля, который в данный момент обрабатывается, показатели физико-механических свойств будут зависеть от данных, полученных в другой скважине. А при определённом уровне схематизации это вносит погрешность в отражение реальной картины. Особенно это характерно для техногенных грунтов.

Для расчётов устойчивости склонов на основе схемы дискретного распределения свойств грунтов задание значений реализуется следующим образом. На геотехническую модель наносятся координаты отобранных из каждой скважины проб. Они определяются в пространстве по абсолютным координатам устья скважины и глубине отбора пробы. На разрез наносятся значения прочностных свойств грунтов в определённой точке. Далее необходимо построить поле распределения параметров, используемых при расчете устойчивости склона. При этом, особую значимость приобретает вопрос выбора и обоснования применяемого метода интерполяции [7].

В данной статье рассмотрено влияние на устойчивость моделируемого склона следующих методов интерполяции прочностных свойств грунтов:

• Метод Чага

Метод предложен Ашоком Чагом (Ashok K. Chugh) – сотрудником службы водных и энергетических ресурсов штата Колорадо, США. Он был впервые опубликован в статье «Pore Water Pressure in Natural Slopes» (поровое давление воды в природных склонах) [8].

• Метод триангуляция Делоне

Метод триангуляции Делоне (TIN triangulation, triangulation irregular network – триангуляция неравномерных сетей) предложен советским математиком Борисом Николаевичем Делоне в 1934 году [9, 10].

• Метод обратных взвешенных расстояний

Метод обратных взвешенных расстояний (Inverse distance) был предложен профессором Гарвардского университета Дональдом Шепардом (Shepard, Donald). Впервые он был опубликован в статье «A two dimensional interpolation function for irregularly spaced data» (двумерная интерполяционная функция для неравномерно распределённых данных) в 1968 году [11].

• Метод тонкого сплайна

Метод тонкого сплайна разработан Ричардом Франком (Franke, Richard) и впервые описан в статье «Thin plate splines with tension» (тонкие сплайны под напряжением), вышедшей в 1985 году [12]. Название «сплайн тонкой пластины» или «тонкий сплайн» (thin-plate spline) отсылает к физической аналогии изгибания тонкого листа металла.

Исходные данные

Оценка зависимости результатов численного анализа опасности развития оползневого процесса от выбранного метода интерполяции прочностных свойств грунтов проводилась на примере расчета устойчивости склона в пределах сферы взаимодействия юго-восточного участка стен и башен XVIII в. Свято-Боголюбского монастыря. В сферу взаимодействия также попадали объекты культурного наследия ЮНЕСКО: Богородице-Рождественский собор, Лестничная башня и переходы палат Андрея Боголюбского. Работы проводились для разработки проекта противоаварийных мероприятий по сохранению объекта культурного наследия - Боголюбского монастыря. В административном отношении участок работ расположен по адресу: Владимирская обл., Суздальский р-н, пос. Боголюбово, Свято-Боголюбский женский монастырь.

В структурном отношении территория проведения изысканий относится к центральной части Московской синеклизы, где с размывом четвертичные отложения залегают на пермских отложениях. В геологическом строении рассматриваемого склона сверху вниз принимают участие современные техногенные накопления (tQ_IV), современные озерно-болотные отложения (lhQ_IV), современные аллювиальные (пойменные) отложения (aQ_IV), нерасчлененные средне-верхнечетвертичные аллювиально-флювиогляциальные отложения первой надпойменной террасы р. Клязьмы (a,fQ_II-III), нерасчлененные средне-верхнечетвертичные флювиогляциальные и озерно-ледниковые отложения (f,lgQ_II-III) и отложения северодвинского горизонта татарского яруса пермской системы (P₂sd).

Известно, что 20 мая 1851 года во время крестного хода в результате оползня обрушился мост. Тогда погибло около 160 человек. В настоящее время активно развивается суффозионный процесс, который наиболее активно проявился 7 лет назад в образовании провала, увеличивающегося размерах на протяжении этого времени. Также периодически происходит сильное замутнение воды в каптированном роднике и, как следствие, заиливание дна купели под этим родником. На поверхности склона присутствуют трещины, поверхность неровная, бугристая (фото.1). В основании склона разгружаются подземные воды.

На этапе изысканий изучение свойств грунтов проводилось стандартными методами на образцах, отобранных в скважинах, пробуренных на склоне и за его пределами [13].

Фото.1 Общий вид оползневого склона – объекта моделирования.

Результаты количественной оценки устойчивости модельного склона

Для оценки зависимости результатов расчётов устойчивости склонов от применяемого метода интерполяции значений прочностных свойств грунтов была выполнена серия расчётов с использованием метода Моргенштерна-Прайса. Данный метод был выбран так как удовлетворяет условиям равновесия моментов и сил [14, 6]. Расчёты производились с применением описанных выше трех схем возможного распределения свойств грунтов в оползневом массиве по круглоцилиндрической поверхности скольжения.

Поля распределения прочностных свойств грунтов в массиве приведены на следующих рисунках:

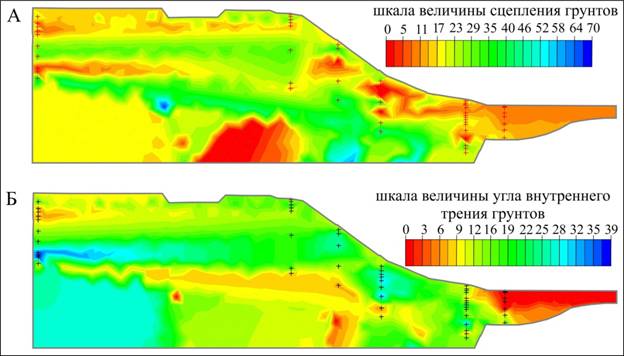
• с использованием метода обратных взвешенных расстояний - рис. 1А и рис.1Б.
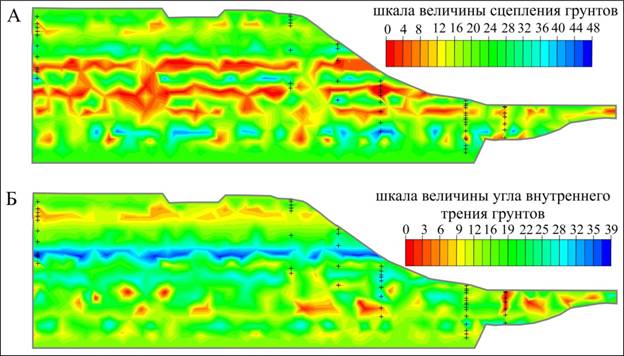
• с использованием метода Делоне – рис. 2А и рис.2Б..
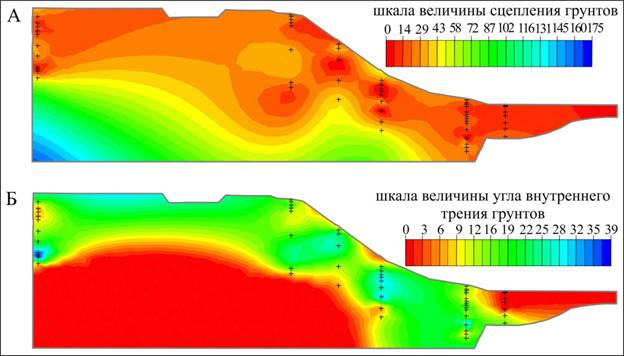
• использованием метода Чага - рис. 3А и рис.3Б.
• с использованием метода тонкого сплайна - рис. 4А и рис.4Б.

 

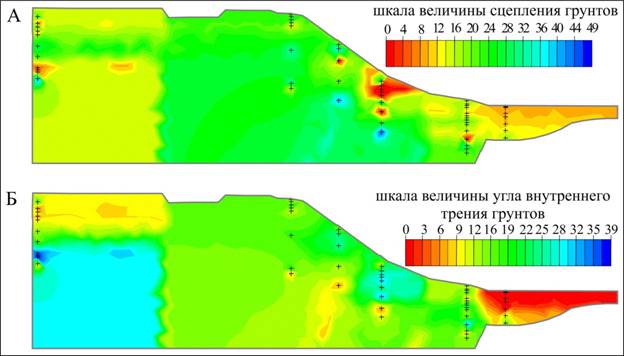
Рис. 1. Поле распределения сцепления (А) и угла внутреннего трения (Б) в массиве по интерполяционному методу обратных взвешенных расстояний.

Рис. 2. Поле распределения сцепления (А) и угла внутреннего трения (Б) в массиве по интерполяционному методу Делоне.

Рис. 3. Поле распределения сцепления (А) и угла внутреннего трения (Б) в массиве по интерполяционному методу Чага.

Рис. 4. Поле распределения сцепления (А) и угла внутреннего трения (Б) в массиве по интерполяционному методу тонкого сплайна.

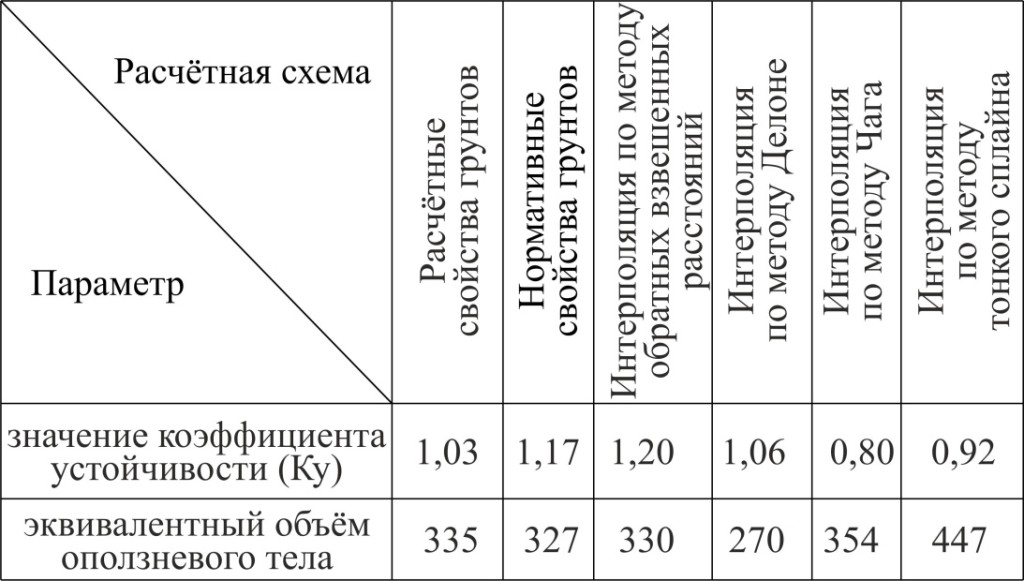
Из полученных результатов видно, что при интерполяции свойств грунтов по методу обратных взвешенных расстояний значение коэффициента устойчивости составило 1,20, эквивалентный объём – 330 м³. Это максимальное значение коэффициента устойчивости при расчётах по данному подходу (таб. 1). При использовании интерполяции по методу Делоне значение коэффициента устойчивости составило 1,06, эквивалентный объём – 270 м³. Это минимальное значение эквивалентного объёма при расчётах по данному подходу. При использовании интерполяции по методу Чага значение коэффициента устойчивости составило 0,80, эквивалентный объём – 354 м³. Это минимальное значение коэффициента устойчивости при расчётах по данному подходу. При использовании интерполяции по методу тонкого сплайна значение коэффициента устойчивости составило 0,92, эквивалентный объём – 447 м³. Это максимальное значение эквивалентного объёма при расчётах по данному подходу.

Таблица 1 – Результаты расчетов устойчивости склона

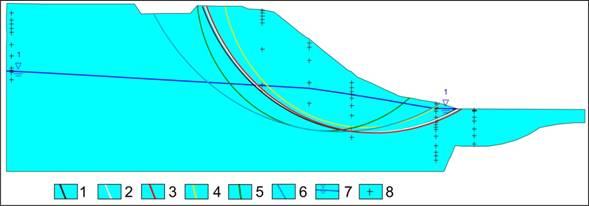
Итоговая сводная геомеханическая схема с результатами расчётов приведена на рисунке 10.

Рис. 10. Итоговая геомеханическая схема.

Результаты расчетов поверхности скольжения: 1-по расчетным характеристикам, 2-по нормативным характеристикам, 3-с использованием интерполяционного метода обратных взвешенных расстояний, 4-с использованием метода Делоне, 5-с использованием метода Чага; 6- с использованием метода тонкого сплайна; 7-уровень грунтовых вод; 8- места отбора проб грунтов.

Обсуждение результатов.

Анализируя расчетные данные можно сделать следующие выводы. Наиболее точные результаты были получены при использовании интерполяционного метода обратных взвешенных расстояний. Это следует из того, что значения эквивалентных объёмов, отличаются от значений, полученных при расчётах по нормативным свойствам грунтов менее чем на 2,5%. То есть, положение потенциальной критической поверхности скольжения совпало практически идеально. Значение коэффициента устойчивости отличается от рассчитанного по нормативным значениям менее чем на 2%. Это говорит о допустимости подобных расчётов.

Расчёты с использованием интерполяционного метода Делоне показали большее расхождение с результатами стандартных расчётов, по сравнению с методом обратных взвешенных расстояний. Это говорит об ограничении возможности его применения на неоднородных склонах. Это связано со сложностью интерполяции значений прочностных свойств грунтов между скважинами, находящимися на большом расстоянии друг от друга. При этом, структура распределения свойств грунтов в массиве сохраняется, как это видно на рисунках 4 и 5.

Расчёты с использованием методов интерполяции Чага и Тонкого сплайна показали нереалистичные результаты, так как коэффициенты устойчивости склона оказались меньше 1. Это говорит о невозможности их применения для расчётов неоднородных склонов, на которых расстояние между скважинами достаточно велико, так как интерполяция значений прочностных свойств грунтов на больших расстояниях между точками опробования приводит к созданию зон с сильно заниженными или завышенными значениями показателей. Экстраполяция свойств грунтов с использованием метода тонкого сплайна приводит к полиноминальному росту значений вне области интерполяции.

Предлагаемые подходы можно применять для расчёта устойчивости склонов, сложенных в верхней части техногенными грунтами. Определение средних значений характеристик для техногена представляет большую сложность в силу неоднородности состава. Задание поля распределения прочностных свойств грунтов в пределах стратиграфо-генетического комплекса техногенных накоплений позволит производить более качественную оценку устойчивости подобных склонов.

Литература

1. Зеркаль О.В., Фоменко И.К. Оценка влияния анизотропии свойств грунтов на устойчивость склонов // Инженерные изыскания.-2013.-№ 9.-С.44-52.
2. Буфеев Ф.К., Кувшинников В.М., Фоменко И.К. Зависимость результатов количественной оценки устойчивости склонов от выбора модели распределения свойств грунтов // Геориск.-2015.-№ 4.-С. 37-42.
3. Krahn. J. Stability modeling with SLOPE/W. An Engineering Methodology.- First Edition, Revision 1.- Calgary, Alberta: GEO-SLOPE International Ltd., 2004.-396 p.
4. Зеркаль О.В., Фоменко И.К. Вероятностная оценка устойчивости склонов и ее использование для анализа оползневой опасности // Анализ, прогноз и управление природными рисками в современном мире: материалы 9-й Международной научно-практической конференции «ГЕОРИСК–2015» (Москва, 13-14 октября 2015 г.).-Москва, 2015.-Т.1-С. 225-231
5. Зеркаль О.В., Фоменко И.К. Влияние различных факторов на результаты вероятностного анализа активизации оползневых процессов // Инженерная геология.-2016.-№1.-C. 16-22.
6. Пендин В.В., Фоменко И.К. Методология оценки и прогноза оползневой опасности. М.: Изд-во РФЛенанд, 2015. 320с.
7. Буфеев Ф.К., Кувшинников В.М., Фоменко И.К. Оценка зависимости результатов расчётов устойчивости склонов на исторических территориях от применяемой модели распределения свойств грунтов в массиве (на примере южного склона Свято-Боголюбского монастыря в Боголюбово) // Одиннадцатая научно-практическая конференция «Перспективы развития инженерных изысканий в строительстве в Российской Федерации» (Санкт-Петербург, 9-11 декабря 2015 г.). - Санкт-Петербург, 2015.
8. Chugh, A.K. Pore Water Pressure in Natural Slopes // International Journal forNumerical and Analytical Methods in Geomechanics/-1981. Vol. 5.-P. 449-454/
9. Делоне Б.Н. О пустоте сферы // Изв. АН СССР.- 1934.- № 4. – С. 793–800.
10. Скворцов А.В. Триангуляция Делоне и её применение.- Томск: Изд-во Том. ун-та, 2002.- 128с.
11. Shepard, D. A two dimensional interpolation function for irregularly spaced data. Proc. 23rd Nat. Conf. 1968, pp. 517-524.
12. Franke, Richard. Thin plate splines with tension // Computer Aided Geometric Design.-1985, Vol. 2, pp. 87 – 95.
13. Бондарев М.В., Буфеев Ф.К., Кувшинников В.М., Фоменко И.К. Комплексирование методов инженерно-геологических исследований при изучении склоновых процессов // Сборник тезисов 6-го Международного научно-практического Симпозиума «Природные условия строительства и сохранения храмов Православной Руси» (Сергиев-Посад, 14-16 сентября 2015 г.).- Сергиев-Посад, 2015.- С.36-38.
14. Slope stability computer program for Morgenstern-Price method of analysis. User's Mantial No. 14 / Krahn. J., Price, V.E., and Morgenstern, N. R. University of Alberta, Edmonton, Alta, 1971.

References

1. Zerkal' O.V., Fomenko I.K. Ocenka vlijanija anizotropii svojstv gruntov na ustojchivost' sklonov // Inzhenernye izyskanija.-2013.-№ 9.-S.44-52.
2. Bufeev F.K., Kuvshinnikov V.M., Fomenko I.K. Zavisimost' rezul'tatov kolichestvennoj ocenki ustojchivosti sklonov ot vybora modeli raspredelenija svojstv gruntov // Georisk.-2015.-№ 4.-S. 37-42.
3. Krahn. J. Stability modeling with SLOPE/W. An Engineering Methodology.- First Edition, Revision 1.- Calgary, Alberta: GEO-SLOPE International Ltd., 2004.-396 p.
4. Zerkal' O.V., Fomenko I.K. Verojatnostnaja ocenka ustojchivosti sklonov i ee ispol'zovanie dlja analiza opolznevoj opasnosti // Analiz, prognoz i upravlenie prirodnymi riskami v sovremennom mire: materialy 9-j Mezhdunarodnoj nauchno-prakticheskoj konferencii «GEORISK–2015» (Moskva, 13-14 oktjabrja 2015 g.).-Moskva, 2015.-T.1-S. 225-231
5. Zerkal' O.V., Fomenko I.K. Vlijanie razlichnyh faktorov na rezul'taty verojatnostnogo analiza aktivizacii opolznevyh processov // Inzhenernaja geologija.-2016.-№1.-C. 16-22.
6. Pendin V.V., Fomenko I.K. Metodologija ocenki i prognoza opolznevoj opasnosti. M.: Izd-vo RFLenand, 2015. 320s.
7. Bufeev F.K., Kuvshinnikov V.M., Fomenko I.K. Ocenka zavisimosti rezul'tatov raschjotov ustojchivosti sklonov na istoricheskih territorijah ot primenjaemoj modeli raspredelenija svojstv gruntov v massive (na primere juzhnogo sklona Svjato-Bogoljubskogo monastyrja v Bogoljubovo) // Odinnadcataja nauchno-prakticheskaja konferencija «Perspektivy razvitija inzhenernyh izyskanij v stroitel'stve v Rossijskoj Federacii» (Sankt-Peterburg, 9-11 dekabrja 2015 g.). - Sankt-Peterburg, 2015.
8. Chugh, A.K. Pore Water Pressure in Natural Slopes // International Journal for Numerical and Analytical Methods in Geomechanics/-1981. Vol. 5.-P. 449-454/
9. Delone B.N. O pustote sfery // Izv. AN SSSR.- 1934.- № 4. – S. 793–800.
10. Skvorcov A.V. Trianguljacija Delone i ejo primenenie.- Tomsk: Izd-vo Tom. un-ta, 2002.- 128s.
11. Shepard, D. A two dimensional interpolation function for irregularly spaced data. Proc. 23rd Nat. Conf. 1968, pp. 517-524.
12. Franke, Richard. Thin plate splines with tension // Computer Aided Geometric Design.-1985, Vol. 2, pp. 87 – 95.
13. Bondarev M.V., Bufeev F.K., Kuvshinnikov V.M., Fomenko I.K. Kompleksirovanie metodov inzhenerno-geologicheskih issledovanij pri izuchenii sklonovyh processov // Sbornik tezisov 6-go Mezhdunarodnogo nauchno-prakticheskogo Simpoziuma «Prirodnye uslovija stroitel'stva i sohranenija hramov Pravoslavnoj Rusi» (Sergiev-Posad, 14-16 sentjabrja 2015 g.).- Sergiev-Posad, 2015.- S.36-38.
14. Slope stability computer program for Morgenstern-Price method of analysis. User's Mantial No. 14 / Krahn. J., Price, V.E., and Morgenstern, N. R. University of Alberta, Edmonton, Alta, 1971.