СРЕДНЯЯ ОБЪЕМНАЯ ПЛОТНОСТЬ АЭРОЗОЛЬНОЙ СУБСТАНЦИИ В ЗАДАЧЕ КОНВЕКТИВНОГО ПЕРЕНОСА

Черёмухина Е.Е.¹, Мосин В.Г.²

¹ Магистрант, ² кандидат физико-математических наук, Самарский государственный архитектурно-строительный университет

СРЕДНЯЯ ОБЪЕМНАЯ ПЛОТНОСТЬ АЭРОЗОЛЬНОЙ СУБСТАНЦИИ В ЗАДАЧЕ КОНВЕКТИВНОГО ПЕРЕНОСА

Аннотация

В статье дается метод расчета объемной плотности загрязняющей аэрозольной субстанции в воздушном потоке. Для этого рассматривается линейная интерполяция двумерного векторного поля на единичном симплексе, после чего строится трехмерное расширение векторного поля, удовлетворяющее условию соленоидальности. В предположении, что выше высоты h загрязнение отсутствует, рассчитывается средняя объемная плотность загрязняющей субстанции в прямой призме высоты h, построенной на симплексе.

Ключевые слова: математическое моделирование, векторное поле, линейная интерполяция, соленоидальность, поток векторного поля, средняя объемная плотность.

 

Cheremukhina E.E.¹, Mosin V.G.²

¹ Undergraduate, ² Assistant professor of Department of Mathematics, PhD in Physics and Mathematics, Samara State University of Architecture and Civil Engineering

THE AVERAGE VOLUME DENSITY OF THE AEROSOL SUBSTANCE IN THE PROBLEM OF CONVECTIVE TRANSPORT

Abstract

The two-dimensional unit simplex is considered. The vector field on the simplex is obtained by linear interpolation. Then the two-dimensional vector field is expanded to three-dimensional vector field on a prism. The solenoidality of expansion is proved.  The volumes of the vector field flux are calculated on the prism. The formula of the average volume density is obtained.

Keywords: math modeling, vector field, linear interpolation, solenoidality, vector field flux, average volume density.

В атмосферном воздухе в большом количестве присутствуют загрязняющие вещества естественного и антропогенного происхождения, к которым, в первую очередь, относятся газообразные вещества и аэрозоли: оксид углерода, двуокись углерода, оксид и диоксид азота, соединения свинца и прочее. Концентрация этих веществ зависит от уровня развития промышленного производства, а перенос происходит вместе с переносом воздушных масс и определяется физико-географическими условиями конкретной местности. Вместе с ростом антропогенной составляющей загрязнений особую актуальность приобретает моделирование переноса загрязняющих атмосферу веществ, которое играет ключевую роль в мониторинге экологической ситуации, а также в ее прогнозировании на основании имеющихся метеорологических данных.

В большинстве работ, посвященных атмосферному переносу аэрозольных субстанций, воздушный поток считается постоянным в любой точке изучаемой области (см., например, [1], [2] или [3]), поэтому интересен вопрос обобщения известных методов на случай, когда поток является функцией координат. Пусть известны значения U(M_i) скалярного поля в вершинах двумерного единичного симплекса S, и пусть они изменяются линейно внутри симплекса. Нетрудно понять, что тогда найдется единственная скалярная функция u(x,y), значения которой в вершинах симплекса совпадут сданными значениями скаляров U(M_i), и кроме того между любыми двумя точками (x₁,y₁) и (x₂,y₂) симплекса S значение функции u(x,y) будет изменяться линейно. Действительно, пусть M_i, — это вершины симплекса S, занумерованные от (0,0) против часовой стрелке: M₁(0,0), M₂(1,0), M₃(0,1). Обозначим U(M_i) = a_i. Тогда скалярные величины U(M_i) задают точки M′₁ (0, 0, a₁), M′₂ (1, 0, a₂), M′₃ (0, 1, a₃) в трехмерном пространстве. Так как точки M_i не лежат на одной прямой, то через точки M′_i проходит единственная плоскость, уравнение которой нетрудно выписать:

.

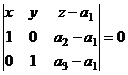(1)

Выражая z, получим следующее:

.

(2)

Это означает, что функция

.

(3)

является той скалярной функцией, которая удовлетворяет заданным нами выше условиям. Векторное поле V(x,y) — это совокупность двух скалярных полей, следовательно полученный выше результат легко можно перенести на двумерный случай. А именно: если известны значения векторов V(x,y), вычисленных  в вершинах единичного симплекса S,, то существует единственная векторнозначная функция υ(x,y)=(υ₁(x,y), υ₂(x,y)), такая что ее значения в вершинах симплекса равны векторам V(М_i), и, кроме того, между любыми двумя внутренними или граничными точками (x₁,y₁) и (x₂,y₂)  симплекса S значения функций υ₁(x,y) и υ₂(x,y) изменяются по линейному закону.

Пусть P — прямая призма высоты h, построенная на симплексе S. Нетрудно убедиться в справедливости следующей теоремы

Теорема 1 Допустим, в вершинах симплекса S зафиксированы следующие значения векторов:

,  ,  .

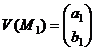(4)

и пусть двумерное векторное поле υ(x,y) на S является линейной интерполяцией этих значений, полученной по формуле (3):

,

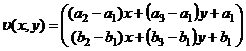(5)

Тогда векторное поле

,

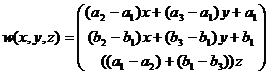(6)

является трехмерным расширением поля υ(x,y) на P и является соленоидальным:

(7)

где σ — это полная поверхность призмы P.

Доказательство. Вычисляя дивергенцию поля, получаем div, но это и означает (7). Теорема доказана.

­Обозначим l_i стороны двумерного единичного симплекса. Занумеруем их от начала координат против часовой стрелки:

, , ,

(8)

обозначим, кроме того, σ_i — боковые грани призмы P на сторонах l_i, пусть σ₀ — нижняя грань, а σ₄ — верхняя грань призмы P, и пусть Ω_i означает плотность загрязняющей аэрозольной субстанции на грани σ_i. Заметим, что объем потока атмосферного воздуха, проходящий через данную поверхность за единицу времени вычисляется как поверхностный интеграл потока по этой поверхности. Поэтому

(9)

Покажем, что справедлива следующее утверждение.

Теорема 2 Пусть выполняются условия теоремы 1. Тогда объемы Ω_i воздушных потоков, проходящих через боковые грани σ_i призмы P за единицу времени, вычисляются по следующим формулам:

,	(10)
,	(11)
,	(12)
,	(13)

кроме того, Ω₀ = 0, положительное значение Ω_i отвечает объему входящего воздушного потока, а отрицательное значение — объему исходящего воздушного потока.

Доказательство. Интерполируем векторное поле V(x,y) по формуле (5):

(14)

Обозначим υ^*(x,y,z) тривиальное трехмерное расширение двумерного поля υ(x,y) с нулевой вертикальной координатой:

(15)

Тогда

(16)

Вычислим сначала объем воздушного потока через грань σ₁.

(17)

где D₁ — это проекция грани σ₁ на плоскость xOz, и последний интеграл в выкладке берется в смысле двойного интеграла по этой проекции. Заметим, что область D₁ является прямоугольником {0 ≤ x ≤ 1; 0 ≤ z ≤ h}, и, кроме того, поверхность σ_i описывается тривиальным уравнением y=0. Поэтому:

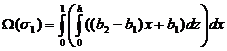(18)

Следовательно,

(19)

Очевидно, что единичный вектор n₁ внутренней нормали к стороне l₁ имеет координаты (0,1). Значит, если b₁+b₂≥ 0, то равнодействующая векторов V(M₁) и V(M₂) образует с ним острый угол, и в этом случае воздушный поток является входящим по отношению к симплексу. Если же b₁+ b₂≤0, то, рассуждая точно так же, устанавливаем, что поток является исходящим.

Далее вычислим следующий объем Ω(σ₂). Для этого воспользуемся формулой (6). Получим:

(20)

здесь D₁ — это проекция грани σ₂ на плоскость xOz, D₂ — проекция грани σ₂ на плоскость yOz, и интегралы в последнем звене выкладки берутся в смысле двойных интегралов. По этим проекциям Снова отметим, что области D_i являются прямоугольниками {0 ≤ x ≤ 1; 0 ≤ z ≤ h}, {0 ≤ y ≤ 1; 0 ≤ z ≤ h}, но поверхность σ₂ описывается на этот раз нетривиальным уравнением x+y=1. Поэтому:

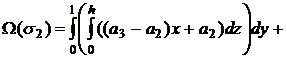
(21)

Проводя необходимые вычисления, получаем:

(22)

Теперь нужно учесть направление воздушного потока в формуле (22), так как эта формула дает лишь абсолютное значение объема, но не его знак. Заметим, что единичный вектор n₂ внутренней нормали к стороне l₂ симплекса S имеет следующие координаты (‑1/, ‑1/). Поэтому, если (a₂+a₃)+(b₂+b₃) ≥0, то равнодействующая векторов V(M₂) и V(M₃) образует с вектором n₂ тупой угол, и поток является исходящим, то есть, объем должен быть отрицательным Поэтому, для учета направления воздушного потока в формуле (22) следует изменить знак на противоположный:

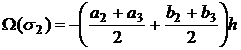(23)

Нетрудно понять, что вычисление объема Ω(σ₃) ничем не отличается от вычислений, уже проведенных нами выше для объема Ω(σ₁), и мы его опускаем. Вычислим  объем . Согласно закону сохранения массы,

(24)

Используем уже вычисленные значения  и, тем самым, получаем требуемое. Теорема доказана.

Стороны симплекса никак не согласованы с направлениями векторов воздушного потока в его вершинах. Для вычисления средней объемной плотности загрязняющей аэрозольной субстанции на симплексе, нам понадобится понятие противоречия между сторонами симплекса и направлениями воздушного потока. Чтобы ввести понятие противоречия, рассмотрим параметрические уравнения сторон симплекса:

.

(25)

Очевидно, что векторное поле υ(x,y), зависящее на симплексе S от двух переменных x и y, на его границах будет зависеть от одной переменной τ. Обозначим υ_i(τ) сужение векторного поля υ(x,y) на i-ю сторону симплекса.

Определение 1 Пусть n_i — внутренний вектор единичной нормали к стороне l_i, симплекса. Функцией противоречия стороны l_i будем называть следующее скалярное произведение:

(26)

Определение 2 Сторону l_i будем называть непротиворечивой, если ее функция противоречия не меняет свой знак:

.

(27)

Если смена знака происходит, будем называть сторону противоречивой.

Несложно доказать следующее утверждение.

Теорема 3 Пусть векторное поле υ(x,y) является линейной интерполяцией векторов V(M_i). Тогда для того, чтобы i-я сторона симплекса S была непротиворечива, необходимо и достаточно, чтобы выполнялось следующее неравенство:

(28)

Доказательство. В силу формул (5) векторное поле v имеет вид:

,

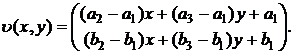(29)

здесь a_i — первые координаты, а b_i — вторые координаты векторов V(M_i). Подставим (25) в (29), выполним необходимые преобразования и получим:

,	(30)
,	(31)
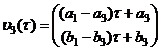.	(32)

С учетом того, что n₁ = (0,1), n₂ = (−1/, −1/), n₃ = (1, 0), вычислим функции противоречия:

,	(33)
,	(34)
,	(35)

Все эти функции монотонны и непрерывны. Поэтому из условия (17) следует условие (16). Обратное следствие очевидно. Теорема доказана.

Определение 3 Симплекс S будем называть непротиворечивым, если все его стороны непротиворечивы. Если хотя бы одна из сторон симплекса противоречива, будем говорить, что симплекс противоречив.

Теорема 4 Пусть симплекс S непротиворечив, пусть на нем линейно интерполировано векторное поле υ(x,y), которое расширено до поля w(x,y,z) на призме P, и пусть объемная плотность загрязняющей атмосферной субстанции постоянна на каждой грани призмы: ρ = ρ_i для грани σ_i.

Обозначим:

(36)

где δ_i(τ) — функции противоречия сторон симплекса. Тогда средняя объемная плотность субстанции в призме P вычисляется по формуле:

,

(37)

где Ω_i — объемы, вычисляемые по формулам теоремы 2.

Доказательство. Симплекс S непротиворечив, поэтому для любой из сторон l_i выполняются условия непротиворечивости, данные в теореме 3. Это означает, что коэффициенты δ_i однозначно определены для любой из сторон l_i, причем значение δ_i = 1 соответствует той грани σ_i призмы P, через которую проходит входящий поток, объем которого положителен. Векторное поле воздушного потока w(x,y,z) в условиях теоремы не зависит от времени. Поэтому объем воздушного потока, который получает призма P за единицу времени постоянен и равен

.

(38)

Объемная плотность загрязняющей атмосферной субстанции также не зависит от времени. Поэтому масса загрязняющей субстанции, которую получает призма P за единицу времени постоянна и равна

.

(39)

Однако на верхней грани σ₄ загрязняющая субстанция отсутствует, и, значит, ρ₄ = 0. Следовательно, выражение (39) не содержит последнего слагаемого:

.

(40)

Итак, каждую единицу времени на входящий объем (38) приходится масса загрязняющей субстанции (40). Поэтому средняя объемная плотность субстанции на призме P вычисляется как отношение:

,

(41)

Теорема доказана.

Литература

1. Мартисон Л. К., Малов Ю. И., Дифференциальные уравнения математической физики: учебник для вузов / Л. К. Мартинсон, Ю. И. Малов. – 2-е изд. – Москва: издательство МГТУ им. Н. Э. Баумана, 2002. – 368 с.
2. Марчук Г. И., Математическое моделирование в проблеме окружающей среды, — М.: Наука, 1982. — 320 с.
3. Ольшанский М. А., Анализ многосеточного метода для уравнений конвекции-диффузии с краевыми условиями Дирихле / М. А. Ольшанский // Ж. вычисл. матем. и матем. физ.— 2004. — т. 44, № 8. — С. 1450–1479.
4. Черёмухина Е. Е., Мосин В. Г. Линии тока линейно интерполированного векторного поля / Е. Е. Черёмухина, В. Г. Мосин // Научное обозрение.— 2015. — № 20. — С. 16–164.
5. Черёмухина Е. Е., Мосин В. Г. Линейно интерполированное векторное поле и выполнение условия соленоидальности / Е. Е. Черёмухина, В. Г. Мосин //Международный научно-исследовательский журнал.— 2015. — Часть 3, № 11. — С. 38–43.

References

1. Martison L. K., Malov Ju. I., [Differential equations of mathematical physics], Differencial'nye uravnenija matematicheskoj fiziki, Moscow: MGTU Baumana Publ., 2002. — 368 p.
2. Marchuk G. I., [Mathematical modeling in environmental problem] Matematicheskoe modelirovanie v probleme okruzhajushhej sredy, — Moscow: Nauka Publ., 1982. — 320 p.
3. Ol'shanskij M. A., [An analysis of the multigrid method for convection-diffusion equations with Dirichlet boundary conditions] Analiz mnogosetochnogo metoda dlja uravnenij konvekcii-diffuzii s kraevymi uslovijami Dirihle, M. A. Ol'shanskij, Computational Mathematics and Mathematical Physics — 2004 — 44:8 — pp. 1374–1403.
4. Cherjomuhina E. E., Mosin V. G. [Current lines of a linearly interpolated vector field] Linii toka linejno interpolirovannogo vektornogo polja, Nauchnoe obozrenie. — 2015. — № 20. — pp. 162–164.
5. Cherjomuhina E. E., Mosin V. G. [Linear interpolation of the vector field and the solenoidality condition] Linejno interpolirovannoe vektornoe pole i vypolnenie uslovija solenoidal'nosti , E. E. Cherjomuhina, V. G. Mosin, Mezhdunarodnyj nauchno-issledovatel'skij zhurnal. — 2015. — № 11. — pp. 38–43.