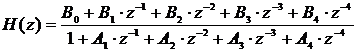РАЗРАБОТКА МОДЕЛИ ДЛЯ РАСЧЕТА КОЭФФИЦИЕНТОВ ЦИФРОВОГО БИХ-ФИЛЬТРА

Мефедова Ю.А.

ORCID: 0000-0001-8917-9200, кандидат технических наук, доцент, Балаковский инженерно-технологический институт Национального исследовательского ядерного университета «МИФИ»

РАЗРАБОТКА МОДЕЛИ ДЛЯ РАСЧЕТА КОЭФФИЦИЕНТОВ ЦИФРОВОГО БИХ-ФИЛЬТРА

Аннотация

В статье рассмотрена разработка Simulink-модели с использованием стандартной библиотеки для расчета коэффициентов цифрового полосового фильтра с бесконечной импульсной характеристикой методом билинейного преобразования, позволяющая автоматизировать данную процедуру без применения дополнительных специализированных библиотек. Результаты работы могут быть использованы при изучении цифровой фильтрации в рамках теории цифровой обработки сигналов студентами технических специальностей высших учебных заведений.

Ключевые слова: моделирование, цифровой фильтр, билинейное преобразование.

 

Mefedova J. A.

ORCID: 0000-0001-8917-9200, PhD in Engineering, Associate professor, Balakovo engineering and technological Institute, National research nuclear University "MEPHI"

DEVELOPMENT OF A MODEL TO CALCULATE THE COEFFICIENTS OF DIGITAL IIR FILTER

Abstract

The article describes the development of Simulink models using the standard library to calculate the coefficients of the digital bandpass filter with an infinite impulse response method, bilinear transform, which allows to automate this procedure without using additional specialized libraries. The results can be used in the study of digital filtering in the framework of the theory of digital signal processing the students of technical specialties of higher educational institutions.

Keywords: modeling, digital filter, bilinear transformation.

Цифровые фильтры широко используются в различных областях как для разделения двух и более распространяющихся совместно сигналов, так и для восстановления сигналов, которые были каким-то образом искажены. При этом цифровые фильтры показывают более высокую точность по сравнению с аналоговыми.

При проектировании фильтров на начальном этапе возникает необходимость расчета его коэффициентов, на основании которых записывается разностное уравнение или передаточная функция, а в дальнейшем рассматриваются вопросы технической реализации. Выбор метода расчета коэффициентов фильтра зависит от его класса. Для фильтров с бесконечной импульсной характеристикой (БИХ), выходные отсчеты которых рассчитываются с учетом как входных (текущих и предшествующих), так и выходных цифровых сигналов, используются следующие методы [1]:

1. Метод размещения нулей и полюсов. Используется для синтеза несложных фильтров. Например, для полосно-заграждающих фильтров, у которых ряд параметров, например, неравномерность в полосе пропускания можно задавать приблизительно.
2. Методы, использующие в своем алгоритме синтез аналоговых фильтров и последующее преобразование в эквивалентные цифровые:

а) метод инвариантного преобразования импульсной характеристики;

б) согласованное z – преобразование;

в) билинейное z – преобразование.

Данная группа методов получила широкое применение. При этом сначала разрабатывается фильтр в аналоговом исполнении с требуемыми желаемыми характеристиками, а затем он преобразуется одним из трех способов в эквивалентный цифровой. Метод (а) после преобразования в цифровой вид повторяет импульсную характеристику спроектированного на начальном этапе аналогового фильтра, но не сохраняет амплитудно-частотную характеристику. Метод (в) сохраняет амплитудно-частотную характеристику, но временные характеристики искажаются. Для частотно-избирательных фильтров самым распространённым является метод, использующий билинейное преобразование, алгоритм которого изложен ниже.

1) На первом этапе проектируется аналоговый фильтр-прототип низких частот. На основании исходных данных строится идеализированная частотная характеристика, которая аппроксимируется с помощью ряда аппроксимирующих функций. В качестве последних могут выступать полиномы и дроби. Полиномиальными функциями являются функции Тейлора (фильтры Баттерворта), Чебышева I типа, а дробными – Кауэра–Золотарева (эллиптические фильтры), Чебышева II типа (инверсная).

Передаточные функции фильтров, построенных на основе полиномов имеют следующие особенности: отсутствуют конечные нули, частотные характеристики не имеют пульсации в полосе задерживания. Передаточные функции фильтров, построенные на основе дробей, в отличии от первых имеют нули на граничных частотах в полосе задерживания, а частотные характеристики – не монотонны в этой полосе. Все фильтры, кроме Баттерворта, в полосе пропускания имеют пульсации. При сравнительном анализе фильтров с различными аппроксимирующими функциями, но с одинаковым порядком, выяснено, что фильтры на основании дают более оптимальные характеристики в полосе затухания.

2) Деформирование граничных или критичных частот. Билинейное преобразование искажает характеристики, поэтому предварительно деформируются все граничные или критичные частоты по формуле:

,

где    Т – период дискретизации.

3) На третьем этапе с помощью частотных преобразований переходят от аналогового фильтра-прототипа низких частот к аналоговому фильтру, с требуемыми частотными свойствами (низкочастотному, высокочастотному, полосовому пропускающему или заграждающему).

4) На последнем этапе к аналоговому фильтру применяется билинейное преобразование с целью получения цифрового. Для этого в передаточной функции аналогового фильтра-прототипа H(s) необходимо сделать подстановку:

Для реализации данного метода могут быть использованы различные математические редакторы. В данной работе предлагается автоматизировать процедуру расчета коэффициентов полосового БИХ-фильтра с аппроксимацией по Чебышеву I типа путем использования разработанной Simulnk-модели. Simulink – это встроенное приложение Matlab, позволяющее в интерактивном режиме осуществлять имитационное моделирование. Модели строятся при помощи готовых блоков из различных библиотек.

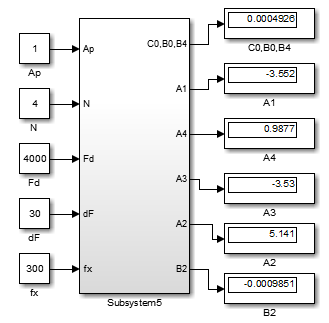
На основании блоков стандартной библиотеки, таких как Sum (Сумматор), Product (Произведение), Divide (Деление), Const (Константа), Trigonometric Function (Тригонометрические функции), Math Function (Математические функции), Display (Дисплей), а также механизма создания подсистем, позволяющего оформить фрагмент Simulnk-модели в виде отдельного блока, разработана модель, общий вид которой представлен на рис.1.

В качестве исходных данных принимаются: Аp - неравномерность в полосе пропускания в дБ, N - порядок фильтра, Fd - частота дискретизации в Гц, dF - ширина полосы пропускания в Гц, fx - центральная частота полосы пропускания в Гц. В выходных блоках после симуляции отображаются коэффициенты передаточной функции фильтра (В1=В3=0):

.

Рис.1 – Общий вид подсистемы

Использование подсистем при разработке модели позволило создать упрощенный интерфейс, в который входят только входные и выходные параметры, необходимые для расчета коэффициентов цифрового фильтра. При этом громоздкие вычисления скрыты от пользователя внутри основной подсистемы, что облегчает восприятие модели.

В разработанной модели внутри основной подсистемы вложены еще четыре подсистемы, каждая из которых отвечает за расчет отдельных параметров, обусловленных алгоритмом метода билинейного преобразования. После расчета коэффициентов строится амплитудно-частотная характеристика, проверяется ее соответствие исходным требованиям и разрабатывается функциональная схема фильтра в прямой, параллельной или каскадной формах. На завершающих этапах проектирования цифровых фильтров выполняется его реализация с помощью программного и/или аппаратного способа.

Реализовать процедуру расчета коэффициентов цифрового фильтра можно также с помощью блока Digital Filter Design, который находится в дополнительной библиотеке DSP Blockset. При проектировании цифровых фильтров с помощью Digital Filter Design открываются более широкие возможности, а именно:

- проектируются фильтры обоих классов (с бесконечной IIR и конечной FIR импульсной характеристикой);

- выбор в каждом классе типа фильтра (Lowpass – ФНЧ, Highpass – ФВЧ, Bandpass – полосовой, Bandstop – режекторный);

- выбор вида аппроксимации (например, для БИХ-фильтров: Butterworth – фильтр Баттерворта, Chebyshev Type I, II – Чебышева I и II рода, Elliptic – фильтр эллиптический (Золотарева-Кауэра);

- кроме коэффициентов фильтра можно визуально наблюдать амплитудно-частотную, фазовую, импульсную и переходную характеристики, картину нулей и полюсов фильтра на комплексной z-плоскости.

Но несмотря на преимущество, имеется существенный недостаток – высокая стоимость данного дополнительного компонента Matlab. Поэтому при его отсутствии разработанная модель может быть достаточно эффективно использована при расчете коэффициентов цифровых полосовых БИХ-фильтров. Также использованный подход может быть применен и для других типов частотно-избирательных фильтров.

Литература

1. Солонина А.И. Цифровая обработка сигналов и Matlab / А.И. Солонина, Д.М. Клионский и др. – СПб.: БХВ-Петербург, 2013.

References

1. 1. Solonina A. I. Digital signal processing and Matlab / I. A. Solonina, D. M. Klionsky and others – SPb.: BHV-Petersburg, 2013.