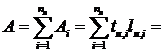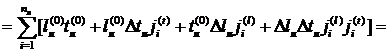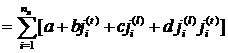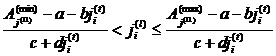ОПТИМИЗАЦИЯ РАЗМЕРОВ ПОПЕРЕЧНОГО СЕЧЕНИЯ ТОНКОСТЕННОГО СТЕРЖНЯ ОТКРЫТОГО ПРОФИЛЯ
Ижендеев А.В.
Доцент, кандидат технических наук, Дальневосточный государственный аграрный университет
ОПТИМИЗАЦИЯ РАЗМЕРОВ ПОПЕРЕЧНОГО СЕЧЕНИЯ ТОНКОСТЕННОГО СТЕРЖНЯ ОТКРЫТОГО ПРОФИЛЯ
Аннотация
Цель исследования – разработка процедуры оптимизации размеров поперечного сечения тонкостенного стержня открытого профиля. Сформулирована задача оптимизации. Параметры оптимизации принимают дискретные значения. Целевая функция – площадь поперечного сечения стержня. Предложена процедура оптимизации, относящаяся к методам сканирования по сетке. Приведен пример оптимизации. Практическое применение исследования – создание систем автоматизированного проектирования оптимальных конструкций.
Ключевые слова: тонкостенный стержень, оптимизация, проектирование.
Izhendeev A.V.
Associate professor, PhD in Engineering, Far Eastern State Agricultural University
OPTIMIZATION OF THE SIZES OF THE CROSS-SECTION OF THE THIN-WALLED ROD WITH AN OPEN PROFILE
Abstract
The purpose of this study is to develop optimization procedures of the sizes of the cross-section of the thin-walled rod with an open profile. In this article, we formulated the optimization problem. The optimization parameters are discrete values. The objective function is the cross-sectional area of the rod. The proposed optimization procedure relates to methods of scanning the grid. The article presents the optimization example. The practical application of the research is the creation of systems of automated design of optimal structures.
Keywords: thin-walled rod, optimization, design.
Постановка задачи. В данной работе объектом исследования является тонкостенный стержень открытого профиля.
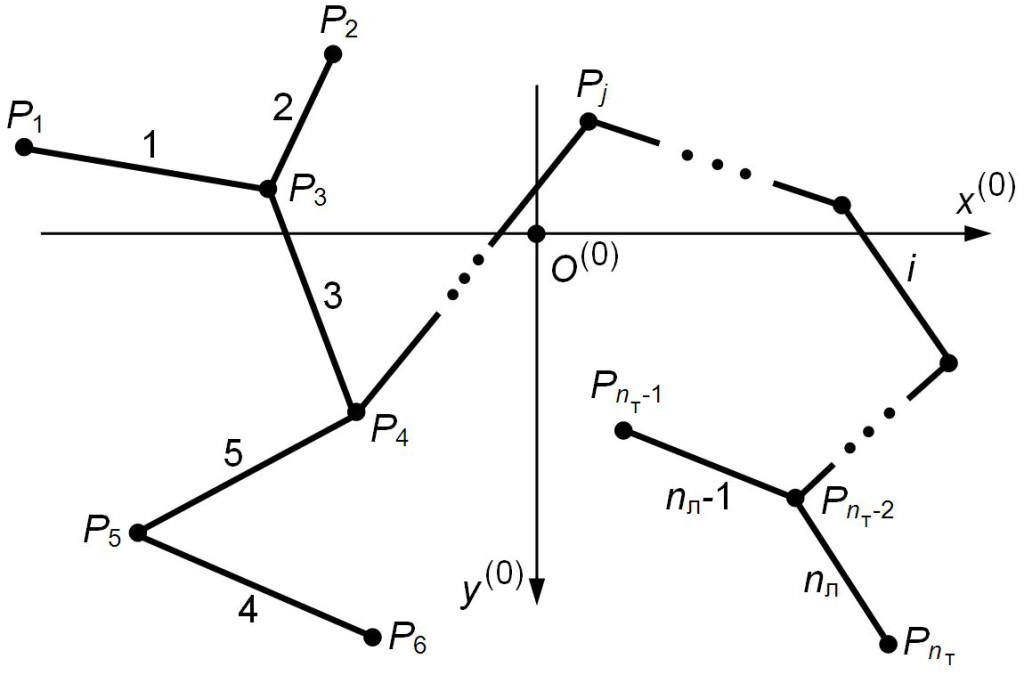
Пусть профильная линия поперечного сечения тонкостенного стержня произвольного по форме открытого профиля состоит из 
отрезков длиной 
, 
, ограниченных 
точками 
, 
(рис. 1).
Рис. 1 – Профильная линия поперечного сечения тонкостенного стержня
Пусть толщина стенки (тонкостенного стержня), расположенной вдоль отрезка 
, равна 
.
Полагаем, что и (параметры проектирования, параметры оптимизации), , принимают дискретные значения.
Возможные сочетания значений и () объединим в множество 
возможных сочетаний параметров проектирования (соответствует множеству возможных или принципиально реализуемых конструкций [1, с. 9, 14]), каждый элемент которого определяет стержень с положительными размерами поперечного сечения стержня и, возможно, с некоторыми дополнительными требованиями к таким размерам. Само это множество может определяться, например, имеющимся в наличии (предполагаемым к использованию) листовым прокатом определенной толщины (из которого будет изготавливаться стержень) или максимально возможными габаритами поперечного сечения стержня (например, исходя из технологических или архитектурных требований).
Требуется найти такие значения и (), при которых площадь 
поперечного сечения стержня является наименьшей и выполняются условия (ограничения) задачи оптимального проектирования (например, условия прочности, общей устойчивости и другие), то есть решение должно принадлежать множеству 
допустимых сочетаний параметров проектирования (соответствует множеству допустимых конструкций [1, с. 9]).
Метод решения. Дискретные значения размеров поперечного сечения стержня зададим формулами:
,
,
где 
и 
– минимально возможные изменения и в процессе оптимизации; 
и 
– целые положительные числа (1, 2, 3 и т. д.); 
и 
– минимально возможные и , уменьшенные соответственно на и .
Площадь поперечного сечения стержня (целевая функция)
,
где
,
, 
, 
, .
Очевидно, что 
– это площадь части сечения, расположенной вдоль отрезка , составляющего профильную линию поперечного сечения стержня.
При постоянных значениях a, b, c и d площадь является функцией двух переменных ( и ):
.
Возможных сочетаний и может быть достаточно много. Предлагается в процессе оптимизации выполнять перебор (сканирование) этих сочетаний упорядоченно.
Для этого зададим такую последовательность множеств 
, 
, 
и т. д. возможных сочетаний и , что значение для каждого элемента любого из этих множеств меньше, чем значение для каждого элемента последующего множества этой последовательности.
Очевидно, что множества 
(
) могут задаваться равенствами и неравенствами, в которые входят и (учтено, что a, b, c и d являются положительными числами):
– с сочетанием 
и 
;
– при 
с такими сочетаниями, что
и 
,
где 
и 
– такие площади, что для каждого элемента из множества справедливо 
(
).
В процессе оптимизации перебор (сканирование) сочетаний и предлагается первоначально вести в множестве , потом – , затем – и т. д. То есть в первую очередь подвергаются сканированию те сочетания, которым соответствует меньшее значение целевой функции, так как по условиям задачи ищется именно ее минимум.
Так как профильная линия поперечного сечения тонкостенного стержня состоит не из одного, а из отрезков, то в процессе оптимизации перебор (сканирование) сочетаний и () предлагается последовательно вести в множествах:
– множество 1 с такими элементами, что 
;
– множество 
(
) с такими элементами, что 
.
Если в некотором из этих множеств впервые находят элементы, соответствующие допустимой конструкции, то среди таких элементов выбирают те, при которых значение целевой функции минимальное. Выбранные элементы соответствуют оптимальной конструкции.
Очевидно, что описанная процедура обеспечивает поиск глобального минимума целевой функции, так как при его поиске анализируются все сочетания и (), при которых площадь поперечного сечения стержня меньше или равна значению целевой функции оптимальной конструкции.
Предложенная процедура перебора сочетаний и () относится к методам сканирования по сетке при решении задач оптимального проектирования. Но такое сканирование не является построчной прогонкой [1, с. 60], которая часто требует немалых затрат времени работы компьютера, а развивает прием, описанный в работе [2, с. 123-125].
В последней из упомянутых работ предлагается предварительно (до процесса перебора и сопутствующего анализа) упорядочивать поперечные сечения стержня (отличающиеся размерами) в порядке возрастания (неубывания) площади этих сечений. Но это потребует (в отличие от предлагаемой в данной работе процедуры), во-первых, дополнительного количества памяти компьютера для хранения результата такого упорядочивания и, во-вторых, дополнительного времени работы компьютера на избыточное упорядочивание сечений, соответствующих хоть и допустимой конструкции, но не оптимальной.
Результаты расчета. В качестве примера рассмотрим оптимизацию центрально сжатого стального стержня, шарнирно опертого в своих концевых поперечных сечениях. Данные для оптимизации взяты из работы [3, с. 15]. Форма поперечного сечения стержня двутавровая с двумя осями симметрии. Параметрами оптимизации являются размеры поперечного сечения стержня: 
– ширина полки (пояса); 
– толщина полки (пояса); 
– высота стенки; 
– толщина стенки. Эти размеры принимают дискретные значения: размеры и кратны 10 мм, а и – 1 мм. Ограничения задачи оптимального проектирования приняты по СП 16.13330.2011 «Стальные конструкции. Актуализированная редакция СНиП II-23-81*». Продольная сжимающая сила 
, расчетные длины элемента 
и 
, расчетное сопротивление стали 
.
В результате оптимизации по предложенной в данной работе процедуре были получены оптимальные размеры: 
, 
, 
и 
. Площадь поперечного сечения стержня при этом составила 
. Такой же результат получен приемом построчной прогонки, что может свидетельствовать о достоверности решения.
В работе [3, с. 15] при тех же исходных предпосылках (за исключением того, что параметры оптимизации принимают дискретные значения) значение целевой функции 
, что отличается от найденного нами решения не более, чем на 1 %. Это согласуется со свойством экстремальной области [1, с. 27]: в окрестности экстремума для конструкций, соответствующих точкам на границе допустимой области, значения целевой функции изменяются весьма незначительно.
Выводы. Предложена процедура оптимизации размеров поперечного сечения тонкостенного стержня открытого профиля в случае, если эти размеры принимают дискретные значения (что естественно для условий реального проектирования).
Предложенная процедура относится к методам сканирования по сетке. Особенностью процедуры по сравнению с приемом построчной прогонки (этот прием также относится к методам сканирования по сетке) является то, что в первую очередь подвергаются сканированию поперечные сечения с меньшей площадью.
Процедура учитывает специфику именно тонкостенных стержней: их поперечные сечения состоят из узких прямоугольников (или могут быть сведены к такой форме).
Процедура позволяет отыскивать глобальный минимум целевой функции.
Литература
- Лазарев, И.Б. Основы оптимального проектирования конструкций. Задачи и методы [Текст] / И.Б. Лазарев. — Новосибирск: Сибирская государственная академия путей сообщения, 1995. — 296 с.
- Лихтарников, Я.М. Вариантное проектирование и оптимизация стальных конструкций [Текст] / Я.М. Лихтарников. — М.: Стройиздат, 1979. — 319 с.
- Путеева, Л.Е. Оптимизация сечений элементов плоских стержневых систем при многопараметрическом нагружении [Текст]: автореф. дис. … канд. техн. наук / Л.Е. Путеева. — Томск: Томский гос. архитектурно-строит. ун-т, 2013. — 24 с.
References
- Lazarev, I.B. Bases of an optimum design of structures. Tasks and methods [Text] / I.B. Lazarev. — Novosibirsk: Siberian State Academy of Means of Communication, 1995. — 296 p.
- Likhtarnikov, Ya.M. Alternative design and optimization of steel structures [Text] / Ya.M. Likhtarnikov. — Mosсow: Stroyizdat, 1979. — 319 p.
- Puteeva, L.E. Optimization of sections of elements of flat rod systems at multiple parameter loading [Text]: authoref. dis. ... cand. techn. science / L.E. Puteeva. — Tomsk: Tomsk State University of Architecture and Building, 2013. — 24 p.