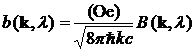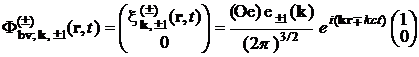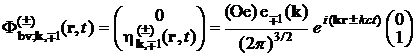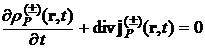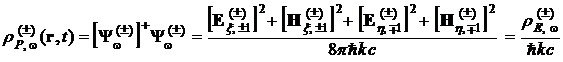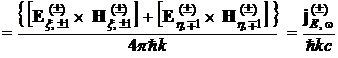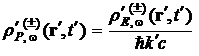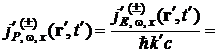Наши журналы
Опубликовать статью Вход и регистрация
Расширенный поиск
Разделы статьи

О РЕЛЯТИВИСТСКОЙ ИНВАРИАНТНОСТИ УРАВНЕНИЯ НЕПРЕРЫВНОСТИ В КВАНТОВОЙ МЕХАНИКЕ ФОТОНА

Научная статья
Давыдов А.П.
Злыднева Т.П.
DOI:
https://doi.org/10.18454/IRJ.2016.46.145
Выпуск: № 4 (46), 2016
Опубликована:
2016/04/18
PDF

Давыдов А.П.1, Злыднева Т.П.2

1 Кандидат физико-математических наук, доцент, 2 Кандидат педагогических наук, доцент, Магнитогорский государственный технический университет им. Г.И. Носова

О РЕЛЯТИВИСТСКОЙ ИНВАРИАНТНОСТИ УРАВНЕНИЯ НЕПРЕРЫВНОСТИ В КВАНТОВОЙ МЕХАНИКЕ ФОТОНА

Аннотация

В статье приводится важное для обоснования квантовой механики фотона доказательство релятивистской инвариантности уравнения непрерывности для плотности вероятности обнаружить фотон в конфигурационном пространстве в случае плоских монохроматических волн. Поскольку такого типа волны инициируют возникновение подавляющей части наблюдаемых интерференционных явлений, в частности в опыте Юнга, подчеркивается, что их теоретическое объяснение с точки зрения квантовой механики фотона имеет релятивистки инвариантных характер.

Ключевые слова: волновой пакет, бивектор, уравнение  Шредингера.

Davydov A.P.1, Zlydneva T.P.2

1 PhD in Physics and Mathematics, Associate professor, 2 PhD in Pedagogy, Associate professor, Nosov Magnitogorsk State Technical University

ON THE RELATIVISTIC INVARIANCE OF THE CONTINUITY EQUATION IN QUANTUM MECHANICS OF THE PHOTON

Abstract

This article provides important for the foundation of photon quantum mechanics the proof of relativistic invariance of the continuity equation for the probability density to detect the photon in configuration space in the case of plane monochromatic waves. Since waves of this kind initiate the occurrence of the majority of the observed interference phenomena, including in the Young’s experiment, it is emphasized that their theoretical explanation from the point of view of photon quantum mechanics has relativistic invariant character.

Keywords: wave packet, bivector, Schrödinger equation.

С момента публикации работы [1] считалось, что для фотона не существует волновой функции в координатном представлении. Однако новые оптические явления требуют рассмотрения одно- и двухфотонных состояний как с методологической точки зрения (квантовая запутанность, нелокальность взаимодействий), так и с практической (квантовые компьютеры, передача информации и др.). В [2–8] предлагалось ввести волновую функцию фотона, нормированную на единичную вероятность, исходя из уравнений Максвелла в форме Майорана для ξ=E+iH и η=E–iH, составленных из напряженностей поля  E и H. Согласно [5–8], она имеет вид

image002,      (1)

где

image004;                                     (2)

(Oe) – единица измерения (эрстед) ξ и η, из которых можно образовать бивектор image006image008 для описания фотона [9]. В [5–8] построен бивектор

image010,   (3)

где верхние знаки индексов соответствуют положительной энергии фотона, нижние – «теоретически возможной» отрицательной; числа image012 отвечают двум возможным значениям спиральности image014;  коэффициенты image016, при первоначальном задании состояния фотона с помощью векторов E и H, однозначно выражаются через эти векторы. Бивекторы image018 описывают состояния с определенными значениями импульса image020, спиральности image014 и энергии image023 фотона и имеют вид

image025,               (4)

image027,               (5)

где image029 – комплексные векторы поляризации.

Функция (1) нормируется на единичную вероятность обнаружить фотон во всем пространстве (в том числе, в детекторе), удовлетворяет уравнению типа Шредингера и уравнению непрерывности [5–8]. Таким образом, осуществляется «первичное квантование» состояний фотона.

В [7–8, 10–11] для иллюстрации функции (1) приводятся результаты однофотонного моделирования лазерного фемтосекундного излучения. При моделировании коэффициенты image031, определяющие импульсное распределение фотона в состоянии (1), задаются в гауссовой форме

image033image035.   (6)

Выясняется, что начальная «шарообразная» форма данного волнового пакета с течением времени трансформируется в некую «конусообразную» форму, напоминая картину излучения Вавилова-Черенкова.

Хотя монохроматические волны, не являются волновыми пакетами, они могут описывать поток фотонов при рассеянии света на веществе. Эти функции можно также применить при объяснении интерференции, нормируя их на один фотон в заданном объеме image037. В пределе image039 выражение (6) устремляет волновой пакет (1) к плоской монохроматической волне, оставляя для нее неизменной нормировку на единичную вероятность. При этом согласно соотношению неопределенностей для энергии и времени [12] будет увеличиваться время image041, в течение которого фотон будет излучен. Время image041, следовательно, играет такую же важную роль, что и время когерентности в классической электродинамике. Однако, о «длине цуга» image044 для одиночного фотона можно говорить теперь с гораздо большей корректностью, чем о длине цуга в классической электродинамике. Действительно, в электродинамике цуг «имеет» материальную основу (в виде «куска» волны, обладающей энергией и импульсом). Попадая, например, на полупрозрачную пластинку, он якобы разделяется на две или больше частей, которые затем интерферируют. Очевидно, что для фотонов такие представления совершенно неприемлемы, поскольку они не могут уменьшить свою частоту, «частично» проходя и отражаясь от пластинки. Фотон может «пойти» по данному пути весь целиком, как показывает опыт, имея первоначальную частоту (и энергию). Для неизмеряемой же напрямую волновой функции вида (1) аналогичное «разделение» ничем не запрещено; измеряется лишь плотность вероятности попадания фотона в данную точку.

Волновая функция (1) удовлетворяет уравнению непрерывности [5–8]

image046,                                    (7)

где

image048,   image050,    (8)

матрица image052, image054 – оператор спина фотона в векторном представлении.

В случае монохроматических волн выражения (8) переходят в выражения

image056,      (9)

image058image060,    (10)

где  image062 и image064 – плотность энергии и плотность потока энергии, задаваемые с помощью (4), (5), например, image066. Составляющие напряженностей в (9), (10) удовлетворяют суперпозиции

image068,  image070            (11)

и приводят к соотношению (аналогичному в классической электродинамике)

image072,                                 (12)

где image074 – единичный вектор вдоль направления распространения волны. При преобразованиях Лоренца для координат и времени

image076 ;    image078 ;  image080 ;  image082 ,                       (13)

где  image084, image086, image088 – скорость системы image090 относительно image092, плотность энергии и плотность потока энергии волны преобразуются как

image094,                           (14)

image096,                       (15)

image098 ,                          (16)

где индекс «image100» соответствует величинам в классической электродинамике. Очевидно, для image062 и image064 имеют место такие же формулы преобразования, за исключением, что в них следует заменить image102 на image104 для отрицательной энергии фотона. Поделив тогда их на image106, используя (9), (10) и формулы преобразования (image108, image110, image112,image114), образующих четырехмерный вектор,

image116,  image118,  image120,  image122,                  (17)

Получим формулы преобразования для плотностей вероятностей:

image124image126,            (18)

image128image130,            (19)

image132,   image134.                (20)

Аналогичные формулы получаются [7] и для «чисто классических» выражений. Формулы (18)–(20) означают, что image136 и image138 образуют 4-вектор в пространстве Минковского, что и доказывает релятивистскую инвариантность уравнения (7).

В заключение отметим, что введение волновой функции фотона позволяет смягчить проблему корпускулярно-волнового дуализма  [6–8, 13].

Литература

  1. Landau L., Peierls R. Quantenelectrodynamik im Konfigurationsraum // Zeit. F. Phys. – 1930. – V. 62. – P. 188-198.
  2. Bialynicki-Birula I. On the Wave Function of the Photon // Acta Phys. Pol. A. – 1994. – V. 86. – P. 97-116.
  3. Sipe J. E. Photon wave functions // Physical Review A. – 1995. – V. 52. – P. 1875-1883.
  4. Давыдов А.П. Квантовая механика фотона // НАУКА И ШКОЛА: тезисы докладов XXXIII научной конференции преподавателей МГПИ / под ред. доц. З.М. Уметбаева. Магнитогорск: Изд-во МГПИ, 1995. – С. 206-207.
  5. Давыдов А.П. Волновая функция фотона в координатном представлении // Вестник МаГУ: Периодический научный журнал. Вып. 5, Естественные науки. Магнитогорск: Изд-во Магнитогорск. гос. ун-та, 2004. – С. 235-243.
  6. Давыдов А.П. Квантовая механика фотона: волновая функция в координатном представлении // Электромагнитные волны и электронные системы. 2015. – Т. 20. - № 5. – С. 43-61.
  7. Давыдов А.П. Волновая функция фотона в координатном представлении: монография. Магнитогорск: Изд-во Магнитогорск. гос. техн. ун-та им. Г.И. Носова, 2015. – 180 с.
  8. Давыдов А.П., Злыднева Т.П. Однофотонный подход к моделированию короткоимпульсного лазерного излучения // Вестник науки и образования Северо-Запада России: электронный журнал, 2015. – Т. 1. - № 4. – URL: http://vestnik-nauki.ru/.
  9. Ахиезер А. И., Берестецкий В. Б. Квантовая электродинамика. – М.: Наука, 1981. – 432 с.
  10. Давыдов А.П. Эволюция в пространстве и во времени волнового пакета фотона фемтосекундного излучения с точки зрения квантовой механики // Современные проблемы науки и образования: тез. докл. XLIII внутривуз. науч. конф. МаГУ. – Магнитогорск: Изд-во МаГУ, 2005. – С. 269-270.
  11. Давыдов А.П. Моделирование распространения в трехмерном пространстве волнового пакета фотона // Актуальные проблемы современной науки, техники и образования: материалы 73-й межд. научно-техн. конф. – Магнитогорск: Изд-во МГТУ им. Г.И. Носова, 2015. – Т. 3. – С. 133-137.
  12. Давыдов А.П. Дисперсионная интерпретация соотношения неопределенностей для энергии и времени и короткоимпульсное лазерное излучение в квазиклассическом подходе // Инновации в науке / Сб. ст. по материалам XXXII междунар. науч.-практ. конф. № 4 (29). – Новосибирск: Изд. «СибАК», 2014. – С. 6-14.
  13. Давыдов А.П. Курс лекций по квантовой механике. Математический аппарат квантовой механики: учеб. пособие / А.П. Давыдов. Магнитогорск: Изд-во Магнитогорск. гос. техн. ун-та им. Г.И. Носова, 2014. – 188 с.

References

  1. Landau L., Peierls R. Quantenelectrodynamik im Konfigurationsraum // Zeit. F. Phys. – 1930. – V. 62. – P. 188-198.
  2. Bialynicki-Birula I. On the Wave Function of the Photon // Acta Phys. Pol. A. – 1994. – V. 86. – P. 97-116.
  3. Sipe J. E. Photon wave functions // Physical Review A. – 1995. – V. 52. – P. 1875-1883.
  4. Davydov A.P. Kvantovaja mehanika fotona // NAUKA I ShKOLA: tezisy dokladov XXXIII nauchnoj konferencii prepodavatelej MGPI / pod red. doc. Z.M. Umetbaeva. Magnitogorsk: Izd-vo MGPI, 1995. – S. 206-207.
  5. Davydov A.P. Volnovaja funkcija fotona v koordinatnom predstavlenii // Vestnik MaGU: Periodicheskij nauchnyj zhurnal. Vyp. 5, Estestvennye nauki. Magnitogorsk: Izd-vo Magnitogorsk. gos. un-ta, 2004. – S. 235-243.
  6. Davydov A.P. Kvantovaja mehanika fotona: volnovaja funkcija v koordinatnom predstavlenii // Jelektromagnitnye volny i jelektronnye sistemy. 2015. – T. 20. - № 5. – S. 43-61.
  7. Davydov A.P. Volnovaja funkcija fotona v koordinatnom predstavlenii: monografija. Magnitogorsk: Izd-vo Magnitogorsk. gos. tehn. un-ta im. G.I. Nosova, 2015. – 180 s.
  8. Davydov A.P., Zlydneva T.P. Odnofotonnyj podhod k modelirovaniju korotkoimpul'snogo lazernogo izluchenija // Vestnik nauki i obrazovanija Severo-Zapada Rossii: jelektronnyj zhurnal, 2015. – T. 1. - № 4. – URL: http://vestnik-nauki.ru/.
  9. Ahiezer A. I., Beresteckij V. B. Kvantovaja jelektrodinamika. – M.: Nauka, 1981. – 432 s.
  10. Davydov A.P. Jevoljucija v prostranstve i vo vremeni volnovogo paketa fotona femtosekundnogo izluchenija s tochki zrenija kvantovoj mehaniki // Sovremennye problemy nauki i obrazovanija: tez. dokl. XLIII vnutrivuz. nauch. konf. MaGU. – Magnitogorsk: Izd-vo MaGU, 2005. – S. 269-270.
  11. Davydov A.P. Modelirovanie rasprostranenija v trehmernom prostranstve volnovogo paketa fotona // Aktual'nye problemy sovremennoj nauki, tehniki i obrazovanija: materialy 73-j mezhd. nauchno-tehn. konf. – Magnitogorsk: Izd-vo MGTU im. G.I. Nosova, 2015. – T. 3. – S. 133-137.
  12. Davydov A.P. Dispersionnaja interpretacija sootnoshenija neopredelennostej dlja jenergii i vremeni i korotkoimpul'snoe lazernoe izluchenie v kvaziklassicheskom podhode // Innovacii v nauke / Sb. st. po materialam XXXII mezhd. nauch.-prakt. konf. № 4 (29). – Novosibirsk: Izd. SibAK, 2014. – S. 6-14.
  13. Davydov A.P. Kurs lekcij po kvantovoj mehanike. Matematicheskij apparat kvantovoj mehaniki: ucheb. posobie / A.P. Davydov. Magnitogorsk: Izd-vo Magnitogorsk. gos. tehn. un-ta im. G.I. Nosova, 2014. – 188 s.