КОМПЛЕКСИРОВАННАЯ ГЕОФИЗИКА МОБИЛИЗАЦИИ НЕФТЕНАСЫЩЕННЫХ КОЛЛЕКТОРОВ МОДЕЛИ ОБОБЩЕННОЙ ВЯЗКОУПРУГОСТИ ПОРОВОЙ ДЕФОРМАЦИИ

Попков В.И.¹, Митина Е.В.²

¹ORCID: 0000-0002-9786-730X, Кандидат физико-математических наук, Самарский государственный технический университет, ²ORCID: 0000-0002-4166-0887, Инженер, СамараНИПИнефть

Работа выполнена при поддержке гранта РНФ № 15-17-00019

КОМПЛЕКСИРОВАННАЯ ГЕОФИЗИКА МОБИЛИЗАЦИИ НЕФТЕНАСЫЩЕННЫХ КОЛЛЕКТОРОВ МОДЕЛИ ОБОБЩЕННОЙ ВЯЗКОУПРУГОСТИ ПОРОВОЙ ДЕФОРМАЦИИ

Аннотация

Миграция в совокупности с динамическими моментами  насыщения оказывает существенное влияние на проницаемость и трещиноватость матрицы, энергетику порового насыщения. Трещиноватость определяет собственные формы накопления диссипативно-резонансной энергии поровой деформации петронасыщения от глубин океанов до гор.  Представлен второй закон Дарси-Фика учета моментов деформации импульсов давления. Показана возможность фокусировки аккумуляции ритмов насыщения на основе пластичного уплотнения вертикально-одноосной трещиноватости.

Ключевые слова: дислокация, сложнопостроенный коллектор, микроструктура, сейсмическая эмиссия, комплексирование

Popkov V.I.¹, Mitina E.V.²

¹ORCID: 0000-0002-9786-730X, PhD in Physics and Mathematics, Samara State Technical University, ²ORCID: 0000-0002-4166-0887, Engineer, SamaraNIPIneft

INTEGRATED GEO-PHYSICS IN OIL-SATURATED RESERVOIR MOBILIZATION MODEL OF GENERALIZED VISCOUS-ELATIC POROUS DEFORMATION

Abstract

Migration in combination with saturation dynamic moments provides significant impact upon the matrix permeability and fracturing, energy of porous saturation. Fracturing defines the characteristic forms of accumulation of dissipative-resonant energy with petro-saturation of porous deformation from the ocean depths to the mountains.   The authors present the second Darcy-Fick’s Law to calculate the deformation moments in pressure pulses. The authors illustrate the possibility to focus saturation rhythms accumulation at the basis of plastic compaction with vertical-single axis fracturing.

Key words: dislocation, complexly structured reservoir, micro-structure, seismic emission, integration.

Для поддержания уровня добычи углеводородов необходимо повышать эффективность разведки и информационных технологий. Необходимо системное научное сопровождение геомоделирования и получения  информации на основе не отдельных законов Дарси, Гука, Ома и т.д., а всей совокупности физико-химических законов развития коллекторов [1, 2].

Системные и научные законы. Геологическая наука характеризуется  множеством закономерностей и геологических законов. Развитие геологии связано с установлением природных законов и 1) системного подхода, 2) принципа иерархичности, 3) структуры геологических систем. Познания в геологии можно ускорить, если применять системную методологию не для усредненных понятий и компиляций различных научных школ и направлений, а для обобщающих теорий, способных увязать в единую цепь ранговые процессы геологических событий [1].

Рис. 1. Многомасштабное сопря-жение синергии геофизических ритмов сверхнизкопроницаемой матрицы осаждения пласта Д3фм  с вертикальной трещиновато-одноос-ной трубкой глубинной миграции,  уходящей в фундамент

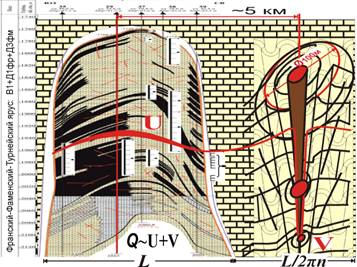
Комплексирование геофизических ритмов является задачей адаптации маршрутов петромиграции океанов и мантии в МАК-волнах Земли. Геодинамические режимы развития циклов сводятся к зарождению в условиях низких значений напряжений горизонтального сжатия и высоких температур, усилению бокового давления и падению температур, разрядке предельно допустимых напряжений надвига и перемещений с ростом температуры, т.е. геодинамическому боковому наращиванию осаждений и напряжений. Таким образом, топологические поверхности геофизических русловых впадин определяются энергетической мобилизацией и разгрузкой сейсмической эмиссии, напряженно-деформируемого состояния континентальной коллизии субдукции, геологических блоков кристаллического фундамента. Они образуются в процессе фокусировки поверхностных сейсмических волн синергии глубинной энергии моментов мантийной деформации. Установлено, что схождение поверхностных волн сопровождается увеличением амплитуд и возрастанием плотности энергии в ней, рис. 2. При фокусировке волн происходит вертикальный разрыв земной коры и образуется расширяющийся к поверхности канал разрушения. Отсутствие идеальной цилиндрической симметрии, обусловленное неоднородностью на пути распространения волн, приводит к их дефокусировке, формированию нескольких центров схождения и образованию поля трубок [3].

Трубки миграции представляют собой вертикальные каналы в земной коре, заполненные породами глубинного происхождения и концентрациями микроэлементов. Поперечные сечения бывают округлой и неправильной формы площадью от 10² до 10⁶ м². С увеличением глубины площадь сечения умень-шается и на глубинах они переходят в дайки и напластования насыщения. Поперечное сечение нижней, корневой части имеет не столь регулярное строение, оно уменьшается, трубка сплющивается и переходит в подводящие дайки. В прилегающей к трубке контактной зоне породы расчленены системами вертикальных, концентрических и радиальных трещин.

Важной особенностью рассматриваемых геологических комплексов является отсутствие признаков термического воздействия на вмещающие породы и наличие их на контактных границах даек и силлов тектонического растяжения. Это означает, что углеводороды внедрились в трубки в холодном состоянии. Рассматривается механизм флюидного брекчирования. Одним из определяющих факторов является водонасыщенная трещиноватость окружающих пород до заполнения, конвективное охлаждение трубки и глубинный выброс.

1 - шельф, 2 - плита материка, 3 - Предуралье, 4 - электро­магнитизм, 5 - петромиграция, 6 - проницаемость, 7 -  осадки, 8 - пласт, 9 - доманик, 10 - миграция, 11 - трещинова­тость, 12 - керн: I - сверхнизкопроницае­мый, II - с каналом, III - прони­цаемый, 13- вертикальная миграция, 14 -  су-перпроводящий пласт Д3фм,Vж  / Vпор - объем прокачки жидкости ~ время Т ~ коэффициент трещиноватости kтр   Рис.  2.   Синергия блочной проводи-мости и проницаемости керна

Подобная синергия обеспечивает супервысокую продуктивность скважин пласта Д3фм Ю.Орловского месторождения. Сверхнизкопроницаемая матрица синергией высокоскоростных ритмов продольной и поперечной волн разуплотнения трещиноватости обеспечивает суммарный дебит скважин, расположенных на прямой линии с трубкой, ~1000 м3/сут несколько лет без снижения давления. Горизонтальная трубка, непрерывно утончаясь, пересекает пласты нижнего девона и переходит в вертикальную трубку фокусировки аккумуляции глубинной энергии. Амплитуды продольных ритмов деформации, взаимоусиливаясь поперечными, поддерживают высокий дебит скважин, расположенных в контуре трубки и на противоположной стороне.

 

Теоретическое обоснование

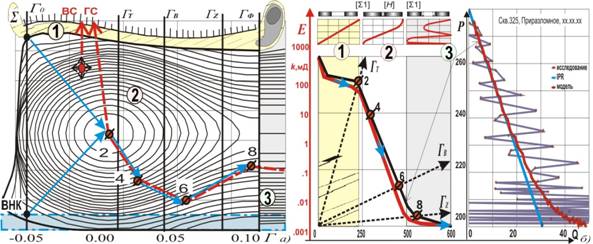
Задачи фильтрации затрагивают фундаментальные вопросы физики природы трения микромира атомарно-молекулярного уровня фазовых и поверхностных слоев  до макромира появления необратимости в изначально обратимых во времени законах и отображения операторов рассеяния. На рис. 3, а) представлен гидродинамический процесс разгрузки потенциалов свободной энергии поверхностей ∑ разупрочнения эллиптических Г_т, параболических Г_в, гиперболических Г_z, туннельных Г_ф структур  и контактов: водо-нефтяного (ВНК) Г₀ , газо-нефтяного (ГНК) - Г_Ф. Разработка горизонтальной (ГС) и вертикальной (ВС) скважинами отображается соответствующей траекторией разгрузки давлений Г_о и Г_ф разуплотненных структур пластично-трещиноватого и упруго-уплотненного двойного порового пространства  стратифицированной залежи. На рис. 3, б) представлена проницаемость туннельной 1, баллистической 2, резонансной 3 микроструктур согласно индикаторной кривой (ИК ø2-8).

Рис. 3 (а) Разгрузка потенциалов свободной энергии порового пространства; (б) проницаемой микроструктуры согласно индикаторной кривой ø2-8

Поверхности разрывов и трещиноватости. На поверхностях разрыва областей непрерывных процессов между характеристиками движения и состояния на различных сторонах должны выполняться некоторые универсальные энергетические соотношения. В непосредственной близости от капиллярной поверхности вязкий слой можно достоверно описать и смоделировать пульсационными и осредненными характеристиками нестационарных уравнений Навье-Стокса. Поровая податливость в малом определяется амплитудными характеристиками поверхности, которые должны быть значительно меньше толщины вязкого подслоя фильтрации. В геологическом времени эволюционной аддитивности напластования решение выйдет далеко за пределы вязкого слоя. При этом за фронтом прохождения волнового решения будет формироваться полностью раздробленное поровое пространство той или иной формации.

 

4D сопряжение вязкого стока и диссипативного осаждения

Представим скорость фильтрации двухслойной области (жидкость+скелет) проницаемого слоя и пульсационной скорости сдвиговой зоны с минимальной скоростью капиллярной пропитки u_* микромасштаба l_*=ν/u_*. Движение несжимаемой жидкости описывается системой уравнений Навье - Стокса для осредненной и пульсационных скоростей и неразрывности [4]

∂u_i /∂t+u_ju_i,_j-‹u_ju_i,_j›+u_jU_i,_j+U_ju_i,_j=-1/ρ∂p/∂x_i+ν∆u_i, u_i,_i=0, νU'=u_*²+‹u_iu_j›.

Здесь ‹u_ju_i,_j›=(u_iu^*_i,_j+u_i^*u_i,_j)/4, ^*- комплексное сопряжение, i, j=x,y,z. Начальные условия U(x,0)=U_o(x). Равновесие  порового скелета описывается уравнениями вязкоупругого движения дифференциального типа и обобщенного закона Гука

σ_ij=µ(ξ_i,j+ξ_j,i)+λδ_ij ξ_i,i ,   σ_ij,j=ρ∂²ξ_i /∂t²,

где λ, µ - обобщенные параметры вязкоупругости. На границах слоев q

σ_ij^q-1n_j|_y=hq=σ_ij^qn_j|_y=hq, ξ_i^q-1|_y=hq=ξ_i^q|_y=hq,

где n - нормаль.  Внешний слой  неподвижный ξ_i|_y=0=0 или свободный σ_ijn_j|_y=0=0. Сопряжение макро- и микромира определяется дополнительными граничными условиями контакта при η=(y-Y₀)/l^*=0: 

u_x=∂ξ_x/∂t, u_y=∂ξ_y/∂t-ξ_y∂U/∂η, -p+∂u_y/∂η =σ_yy/ρu^*2,   ∂u_x/∂η+∂u_y/∂x =σ_xy/ρu^*2.

Здесь переменные безразмерные. Гармоническая модель вязкоупругости определяется модулями сдвига µ и упругости λ

µ(ω)=μ_o+Σⁿ_j=1μ_j(ωτ_j)²/(1+(ωτ_j)²) - iΣⁿ_j=1μ_jωτ_j /(1+(ωτ_j)²),  λ(ω)=λ_o-2/3(µ(ω)+μ_o),

статическими модулями µ_o, λ_о, функцией релаксации µ(t)=µ_o+Σⁿ_j=1μ_j·e^-t/τj со спектром τ_j . Система уравнений при пренебрежении квадратичными членами пульсаций скорости допускает решение в виде волн F_j=F_j(y)exp i(k_xx+k_zz-ωt),  где F_j=u_j,p. Решение для скоростей и давления записывается

u_j(η)=1/k∫G_j(t)sh[k(η-t)]dt+C_je^-kη,  p(η)=1/ik∫G(t)sh[ik(η-t)]dt+C₄e^-ikη.

Здесь G_x=Θ_x+u_yU_x'+ik_xp, G_y=Θ_y+p', G_z=Θ_z+ik_xp, Θ_i=-i(kU_i-ω)u_i, G=-ik_xU_x'u_y. Из условия сопряжения скоростей пульсаций и Дарси U=1/æ ln η+C_æ находим æ=1/R₀U'(R_o), C_æ=U(R₀)-ln R_o/æ.

Поровая деформация генерирует касательные напряжения, которые при τ_ω ≥ ρu_*² создают тягу. Усиления деформации проявляются на границах торможения формаций и упругого уплотнения скелета, где вторые моменты микроуровня и резонансных частотах становятся очень большими. Сыпучие слои при фазовых скоростях С/a_μ > 1 при ω > ω_s способны  индуцировать только отрицательные, снижающие сопротивление трения, напряжения Рейнольдса во всем вязком слое. Амплитуды поверхностей подобных типов значительно больше вязкого слоя, а в районе собственной частоты ω_k ~1 - в несколько десятков раз. Смена знака напряжений указывает на изменение поляризации петромагнитизма или гидрофобности и гидрофильности, на пластичный разрыв и развитие трещиноватости.

Предельные значения сложной реологии уплотнения структур порового пространства учитываются представленным вторым законом Дарси-Фика зависимости средней скорости фильтрации от градиента давления и скоростей пульсации поровой деформации     U=λ·grad(p-p_cow-ρgh) - D∆u, где p_cow – капил-лярное давление, λ - проводимость, D - коэффициент диффузии.

 

Выводы

Осредненный вязкий сток переходит в геофизическую синергию диффузионно-диссипативной пропитки при скоростях U=35u_min~35·10^-7 м/сек независимо от вида геологической границы.

При частотах ω ≥ ω_s единица длины колеблющейся поверхности обеспечивает компенсацию вязкого сопротивления трения. Формируются резонансно-сверхпроводящие импульсные выбросы туннелирования формаций, эволюционных переходов энергетических уровней.

Структурно-феноменологические формы капиллярно-молекулярного движения деформируемой поровой микроструктуры соответствуют всем открытым на данный момент феноменам физико-химических форм взаимодействия вещества. Для частного случая напряженно-деформируемого состояния гидродинамики поровой фильтрации в сплошной среде это соответствует мультифазовым траекториям вязких, пластичных и упругих фазовых движений.

Литература

1. Казанцева Т.Т. Научные законы геологического развития. - Уфа. - Гилем. - 2006. - 74 c.
2. Попков В.И., Шакшин В.П. Интегрированное геолого-гидродинамическое моделирование в системном управлении разработкой нефтегазовых месторождений // Вест. СамГТУ.- № 1(18).- 2009 - c. 239-250.
3. Белов С.В., Фролов А.А. Посланцы мантийных магм // Природа. - № - 1998 - с. 44-56.
4. Popkov V.I., Astafiev V.I., Shterenberg A.M., Khamitov I.G., Kolesnikov V.A, Popkova A.V. Global Hydrocarbon Energy Potential of Euro-Asia or Solution of Navier-Stokes Equation for Deformed Micro-Structure of the Earth’s Porous Space // Modern Applied Science. - № 9(9). - 2015 - pp. 307-321.

References

1. Kazantseva Т.Т. Scientific Laws of Geological Development. - Ufa. - Gilem. - 2006. - 74 p.
2. Popkov V.I., Shakshin V.P. Integrated Geological and Hydro-dynamic Modeling and System-like Monitoring over Oil and Gas Field development // Bulletin of Sam STU.- issue 1(18). - 2009, - pp. 239 - 250.
3. Belov S.V., Frolov А.А. The Agents of Mantle Magma // Nature. -11. -1998, - pp. 44 - 56.
4. Popkov V.I., Astafiev V.I., Shterenberg A.M., Khamitov I.G., Kolesnikov V.A, Popkova A.V. Global Hydrocarbon Energy Potential of Euro-Asia or Solution of Navier-Stokes Equation for Deformed Micro-Structure of the Earth’s Porous Space // Modern Applied Science. - № 9(9). - 2015 - pp. 307-321.