ИССЛЕДОВАНИЕ ПРОЦЕССА ПРОХОЖДЕНИЯ ПОПЕРЕЧНОЙ СЕЙСМИЧЕСКОЙ ВОЛНЫ ЧЕРЕЗ ГРУНТОВОЕ СЛОИСТОЕ ОСНОВАНИЕ

Чукин Р.Б.

Аспирант, Институт геомеханики и освоения недр Национальной академии наук Кыргызской Республики

ИССЛЕДОВАНИЕ ПРОЦЕССА ПРОХОЖДЕНИЯ ПОПЕРЕЧНОЙ СЕЙСМИЧЕСКОЙ ВОЛНЫ ЧЕРЕЗ ГРУНТОВОЕ СЛОИСТОЕ ОСНОВАНИЕ

Аннотация

В статье приводятся результаты исследования прохождения поперечной сейсмической волны, через слоистое грунтовое основание, представленное численной моделью грунтовой колонны. Теоретическая значимость данных исследований заключается в возможности наглядно изучить эффекты, возникающие в результате отражения сейсмических волн от границ раздела различных грунтов и влияние этого процесса на характеристики колебаний поверхности. Приводятся результаты многофакторного анализа на примере трехслойного грунтового основания. Практическая значимость данного анализа заключается в том, что он позволяет исследовать факторы, влияющие на колебания поверхности при землетрясении, что может помочь в обеспечении сейсмической устойчивости возводимых сооружений.

Ключевые слова: скорость, частота, импульс, колебание.

Chukin R.B.

Postgraduate student, Institute of geomechanics and mineral resources development of Kyrgyz Republic National academy of science

RESEARCH OF SEISMIC SHEAR WAVE PROPAGATION PROCESS THROUGH SOIL LAYERED FOUNDATION

Abstract

The paper gives the results of seismic shear wave propagation research through layered soil foundation represented by numerical model of soil column. Theoretical importance of these researches is in possibility visually exploring the effects resulting from reflection of seismic waves from soil boundaries and influence of this process on the surface motions characteristics. The results of multifactor analysis are given on example of soil foundation which consists of three layers. Practical importance of this analysis is that it allows research the factors affecting on surface motion during earthquake that can help to provide seismic stability of constructed facilities.

Keywords: velocity, frequency, impulse, motion.

Для оценки сейсмической устойчивости сооружений, например грунтовых дамб, возведенных на слоистом основании необходимо исследовать влияние местных грунтовых условий на колебания поверхности при землетрясении. Влияние местных грунтовых условий на изменение характеристик колебаний поверхности площадки строительства сооружения при землетрясении является результатом сложного процесса прохождения сейсмических волн. На результирующий сейсмический эффект площадки строительства влияют параметры исходной сейсмической нагрузки и характеристики слоев грунта залегающих в основании. При определенных грунтовых условиях может возникать динамическое усиление или ослабление в виде изменения величины пикового ускорения или продолжительности колебаний. Слои залегающего грунта способны изменять частотные характеристики колебаний приходящей к ним сейсмической волны. Результатом таких изменений может быть усиление колебаний на определенных частотных диапазонах, которые могут совпадать с собственными частотами возведенного сооружения. Подобное совпадение приводит к эффектам резонанса. Во время землетрясения Лома Приета в Сан-Франциско 17 октября 1987 года было отмечено 6-10 кратное увеличение амплитуд колебаний на поверхности глинистых грунтов по сравнению со скальным основанием на частоте 1 Гц и 2-3 кратное для частотного диапазона 3-5 Гц. Собственные частоты большинства разрушенных сооружений составляли 2-3 Гц. При землетрясении в Мехико 1985 года в отдельных частях города резонансное усиление сейсмических колебаний с частотой около 0,5 Гц достигало 75 раз, что привело к избирательному разрушению высотных зданий с близкими резонансными частотами и гибели 10000 человек [1].

Оценка влияния грунтовых условий площадки строительства сводится к изучению трех основных параметров сейсмических колебаний: уровень амплитуд, доминантная частота и продолжительность. Последний фактор может иметь решающее значение для устойчивости некоторых сооружений. Существуют примеры, когда кратковременная сейсмическая нагрузки с высоким значением ускорений оказывалась неопасной для многих сооружений. При Калифорнийском землетрясении 27 июня 1966 года максимальные горизонтальные ускорения на поверхности достигали 4,9 м/сек² (0,5 g), но из-за кратковременной продолжительности существенных повреждений сооружений не наблюдалось [2]. И наоборот, колебания с невысокой амплитудой, но с продолжительностью до нескольких десятков секунд могут привести к значительным разрушениям. Землетрясение в Мехико 28 июля 1957 года имело невысокие максимальные горизонтальные ускорения 0,49-0,98 м/сек² (0,05-0,1 g), на за счет продолжительности более 90 секунд практически полностью разрушило центр Мехико [3].

Основная цель данной статьи – исследование процесса распространения сейсмических волн в слоистом грунтовом основании, приводящего к изменениям основных параметров сейсмических колебаний. Для достижения данной цели были поставлены и решены следующие задачи: выполнено численное моделирование прохождения сейсмической волны, через слоистое грунтовое основание, представленное колонной, анализ и изучение процесса прохождения сейсмической волны и возникающих особенностей; исследование факторов влияющих на динамическое усиление колебаний поверхности и выявление закономерностей.

Наиболее важными для оценки сейсмической устойчивости сооружений являются поперечные упругие сейсмические волны, так же известные в зарубежной литературе как упругие волны сдвига или вторичные S-волны. Исследования их влияния на колебания поверхности в натурных условиях является дорогостоящим и сложным в реализации мероприятием. Моделирование с проведением численных экспериментов позволяет обойтись меньшими затратами, а так же наглядно выявить особенности, связанные с прохождением S-волн через слоистое грунтовое основание. Для выполнения численных экспериментов была создана модель основания в кодах программы FLAC 7, представляющая из себя колонну высотой 50 метров и шириной 1 метр. Данная модель используется как численная экспериментальная установка, для изучения изменения горизонтальных скоростей в грунтовых основаниях от приложения к ее основанию касательного напряжения в официальных инструкциях к программе FLAC 7 [4].

Выявление особенностей влияния геологического строения основания на прохождение S-волны проводилось на трех видах моделей:

1. однородное скальное основание мощностью 50 метров;
2. двухслойное основание, состоящее из 35 метрового слоя скальной породы и 15 метрового слоя глинистого грунта;
3. трехслойное основание, состоящее из 35 метрового слоя скальной породы, глинистого прослоя мощностью 10 метров и 5 метрового поверхностного слоя песчаного грунта.

Согласно методологии описанной в инструкциях к программе FLAC 7 воздействие S-волны задавалось путем приложения касательного напряжения к нижней границе колонны. Величина касательного напряжения рассчитывается по формуле:

                                                                              (1)

где:  - плотность скальной породы;  – скорость распространения S-волн в скальной породе;  – тангенциальная скорость на границе основания.

По условию экспериментов основанию колонны передается импульс напряжения, вызывающий амплитуду скорости горизонтального смещения (СГС) основания с максимальным значением 1 м/сек. Значения  изменяются от 0 до 1 и определяются функцией синусоиды со сдвигом  от начала координат  времени   по зависимости:

                                                        (2)

где:  - частота импульса в Гц.

Частота  принимается равной 100 Гц. Такое высокое значение было выбрано для того, чтобы можно было наглядно проследить за тем как S-волна проходит через тело колонны. При более реальных значениях частоты прикладываемого импульса, например 4 Гц, S-волна мгновенно проходит тело колонны, не позволяя исследовать процесс распространения S-волны.

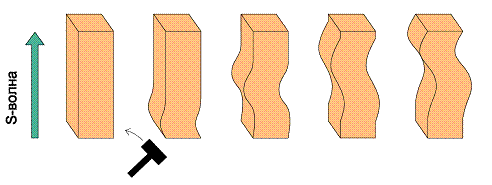
Особенностью моделирования является приложение однопикового воздействия S-волны и то, что касательные напряжения имеют однонаправленное приложение имитирующее удар. Схема приложения импульса напряжения и поведение колонны представлены на рисунке 1. В численных экспериментах колонна моделируется без дополнительного динамического затухания, что позволяет более наглядно проследить за изменением СГС вдоль тела колонны при прохождении S-волны.

В качестве скальной породы был принят гранит. Расчетные свойства гранита были приняты следующими: плотность 2700 кг/м³; скорость распространения продольных упругих волн 4500 м/сек; скорость распространения упругих поперечных волн 2250 м/сек [5].

Динамические модули упругости сдвига и объемных деформаций были получены из зависимостей:

                                                            (3)

где:   – скорость распространения упругих продольных волн;  - скорость распространения упругих поперечных волн;  – динамический модуль упругости объемных деформаций;  – динамический модуль упругости деформаций сдвига.

Рис. 1 - Схема приложения импульса напряжения и смещения колонны

Граничные условия численной модели заданы так, что основание жестко зафиксировано, а вершина может свободно колебаться. Основанию модели так же была задана вязкая поверхность затухания, которая полностью поглощает приходящие к ней отраженные волны. Значения СГС наблюдались в трех контрольных точках численной модели колонны: 1 – в основании колонны; 2 – в середине колонны; 3 – на вершине колонны. Положение контрольных точек во всех численных экспериментах не менялось.

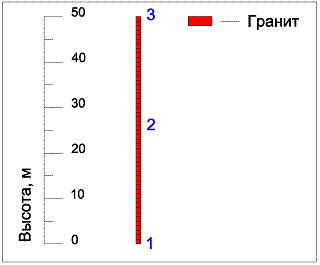
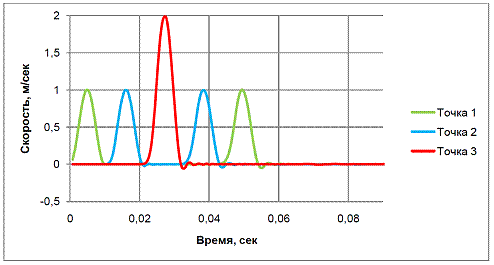
Численная модель первого эксперимента с контрольными точками наблюдения СГС показана на рисунке 2. На рисунке 3 показаны графики изменения СГС при прохождении S-волны во времени. Из рисунка видно, что амплитуда СГС основания колонны равна 1 м/сек. S-волна прошла от границы основания до вершины за 0,0275 секунды и вернулась обратно с той же скоростью к границе основания. В контрольной точке 2 СГС начала возрастать в то время, когда в контрольной точке 1 снизилась до 0.

Рис. 2 - Численная модель первого эксперимента

Амплитуды скоростей в этих двух контрольных точках одинаковы по значениям. СГС вершины колонны увеличилась в два раза, и составила, 2 м/сек. Две последующие линии характеризуют СГС в контрольных точках 2 и 1, вызванные отраженной S-волной от свободной поверхности колонны. После того, как S-волна вернулась в основание колонны, вязкая поверхность затухания поглощает ее. Подобное поглощение можно ассоциировать с бесконечной средой. Амплитуды СГС в контрольных точках 2 и 1 от отраженной волны идентичны и равны половине амплитуды СГС вершины колонны.

Рис. 3 - Графики изменения СГС в теле колонны, первый эксперимент

Гранитная колонна от прохождения однонаправленной S-волны практически не совершает колебательных движений. На это указывают графики СГС, которые не имеют существенных отрицательных значений.

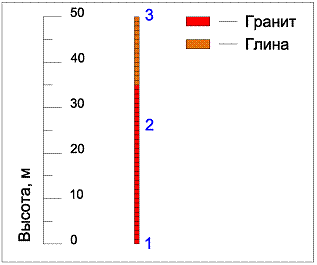
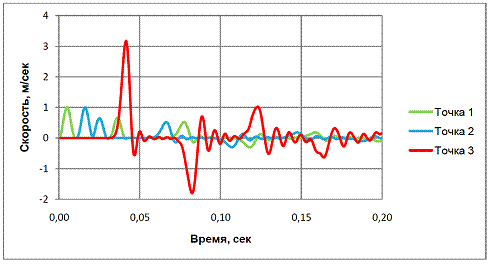
Во втором численном эксперименте свойства 35-ти метрового гранитного слоя и величина прикладываемой нагрузки остается такой же, как для первого эксперимента. Глинистый прослой мощностью 15 метров над гранитным основанием имел следующие свойства: плотность 1800 кг/м³; скорость распространения продольных упругих волн 1500 м/сек; скорость распространения упругих поперечных волн 750 м/сек. Динамические модули упругости для глины были определены из зависимостей (3). Численная модель второго эксперимента показана на рисунке 4. На рисунке 5 показаны записи СГС от приложенного воздействия. Для анализа были рассмотрены записи СГС в теле колонны за 0,2 секунды прохождения S-волны. Характер СГС в колонне, состоящей из двух материалов, поменялся по сравнению с характером СГС в однородной колонне. Время прохождения S-волны от границы основания до вершины колонны увеличилось до 0,042 секунды. Наблюдается колебание вершины колонны. Амплитуды СГС в контрольных точках 1 и 2, которые расположены в граните, идентичны первому эксперименту и равны 1 м/сек. S-волна, подходя к глинистому слою, отражается от него и делится на две составляющие, первая из которых движется обратно к основанию, а вторая продолжает движение к вершине. Последующие две кривые на графике СГС в контрольных точках 1 и 2 это скорости отраженной волны, которая, доходя до основания колонны, полностью затухает. На вершине колонны происходит увеличение СГС, до 3,17 м/сек. Отраженная S-волна от свободной поверхности возвращается вниз к основанию. Доходя до основания глинистого слоя, S-волна вновь делится на две составляющие. Первая, из которых, продолжает двигаться к основанию, а вторая отраженная возвращается к вершине колонны. Вершина колонны свободно колеблется в обоих направлениях. График записанной СГС в точке 3 на вершине колоны указывает на то, что S-волна «гуляет» в глинистом слое вверх и вниз, отражаясь то от свободной поверхности, то от

Рис. 4 - Численная модель второго эксперимента

Рис. 5 - Графики изменения СГС в теле колонны, второй эксперимент

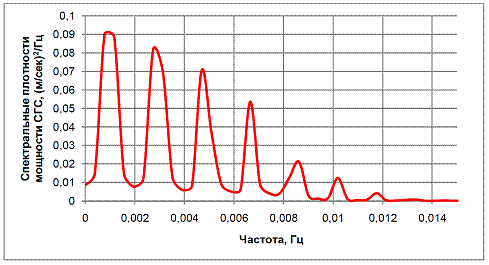
границы раздела грунтов. При отражении от границы грунтов каждый раз часть S-волны уходит к основанию, о чем говорят последующие затухающие графики СГС в точках 1 и 2. Колебания вершины по истечении времени затухают. Из графиков СГС на вершине колонны видно, что образуются колебания различной частоты. Был построен график спектральной плотности мощности СГС в точке 3. Данный график изображен на рисунке 6. Он наглядно показывает наличие семи частот колебаний от приложения нагрузки одной частоты. Общая продолжительность колебания вершины колонны увеличилась и составила примерно 0,5 секунды.

Рис. 6 - Спектральные плотности мощности СГС вершины колонны, второй эксперимент

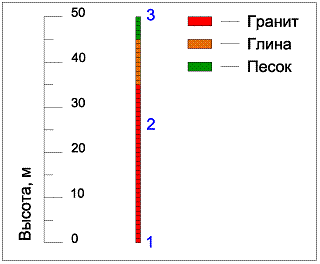
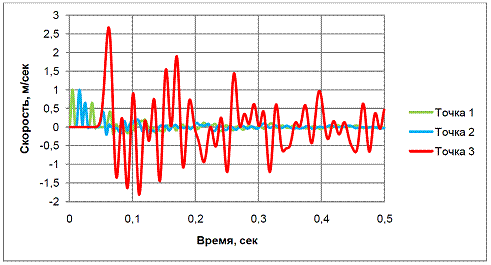
В третьем численном эксперименте колонна представлена 35 метровым гранитным слоем, глинистым слоем мощностью 10 метров и 5 метровым слоем рыхлого песка над глинистым слоем. Свойства песка, при которых выполнялись расчеты, имели следующие значения: плотность 1500 кг/м³; скорость распространения продольных упругих волн 400 м/сек; скорость распространения упругих поперечных волн 200 м/сек. Численная модель третьего эксперимента показана на рисунке 7. Динамические модули упругости для песка были определены из зависимостей (3). Свойства гранита и глины не изменялись. СГС наблюдались в контрольных точках колонны, как и при двух предыдущих экспериментах. На рисунке 8 показаны записи СГС в контрольных точках 1, 2 и 3 за 0,5 секунды расчета. Из рисунка видно, что наличие третьего песчаного слоя значительно изменило характер колебаний вершины колонны. Пиковое значение амплитуды СГС вершины меньше, чем во втором эксперименте и составляет 2,67 м/сек, но амплитуда СГС последующих колебаний от отраженных S-волн гораздо выше. Основной отличительной особенностью от второго эксперимента является то, что отраженная S-волна от поверхности, доходя до кровли глинистого грунта, отражается и возвращается вновь к вершине колонны. Тем самым, проявился эффект «ловушки» песчаного слоя. Об этом говорит очень небольшая амплитуда колебаний СГС возвращающихся к основанию модели, в то время как на поверхности амплитуда остается достаточно высокой, а так же вершина колонны колеблется намного дольше.

Рис. 7 - Численная модель третьего эксперимента

Рис. 8 - Графики изменения СГС в теле колонны, третий эксперимент

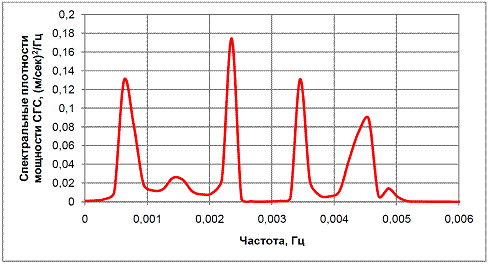
Общая продолжительность колебания вершины увеличилась и даже после 5 секунд расчета не стабилизируется. График спектральной плотности мощности СГС в точке 3 показан на рисунке 9. График спектральной плотности мощности СГС указывает на изменение частоты колебаний.

Рис. 9 - Спектральные плотности мощности СГС вершины колонны, третий эксперимент

Был выполнен многофакторный анализ трехслойной грунтовой модели используемой в третьем эксперименте для оценки влияния мощности грунтовых слоев и скорости прохождения упругих поперечных волн в них, на смещения, скорости смещения и пиковое ускорение на вершине колонны. Для многофакторного анализа была использована математическая теория планирования эксперимента (МТПЭ). МТПЭ посвящено значительное количество научной литературы [6, 7]. В выполненных исследованиях была использована версия МТПЭ реализованная в программе Statistica. Методика выполнения численных экспериментов для многофакторного анализа аналогична предыдущим исследованиям распространения S-волны в слоистой грунтовой колонне, за исключением частоты прикладываемого импульса. В исследовании процесса прохождения S-волны значение частоты импульса было выбрано 100 Гц, для получения более достоверных результатов многофакторного анализа частота импульса была понижена до реалистичных 4 Гц.

В качестве варьируемых факторов были выбраны мощность песчаного слоя, обозначенная как h_песок; мощность глинистого слоя, обозначенная как h_глина; и скорости распространения упругих поперечных волн в этих грунтах, обозначенные как V_s_песок и V_s_глина соответственно. Мощность песчаного слоя h_песок варьировалась от 2 до 6 метров. Мощность глинистого слоя h_глина от 4 до 10 метров. Скорость распространения упругих поперечных волн в песчаном слое V_s_песок варьировалась от 250 до 450 м/сек, а в глинистом слое V_s_глина от 150 до 450 м/сек. Диапазоны варьирования V_s_песок и V_s_глина были выбраны из литературы [8]. В качестве отклика были выбраны: СГС вершины колонны, горизонтальные смещение вершины колонны (ГС), пиковые горизонтальные ускорения вершины колонны (ПГУ). Матрица планирования эксперимента приведена в таблице 1.

Достоинством МТПЭ реализованной в программе Statictica является вычисление и графическое представление силы влияния варьируемых факторов и их взаимодействия на отклик. Сила влияния представляется в виде карты Парето. На рисунке 10 приведена карта Парето для отклика СГС вершины колонны.

Вертикальная красная линия разделяет варьируемые факторы и их взаимодействие на значимые и не значимые. Если фактор пересекает вертикальную кранную линию, это означает, что фактор значим. Чем сила влияния фактора больше, тем длинней его составляющая. На СГС вершины колонны наибольшее влияние оказывает скорость распространения упругих поперечных волн V_s_глина в глинистом прослое со знаком минус. Знак минус означает, что при снижении значения V_s_глина СГС вершины колонны увеличивается.

Рис. 10 - Карта Парето для отклика СГС вершины колонны

На втором месте по значимости стоит мощность глинистого слоя h_глина с положительным знаком. Чем больше мощность глинистого прослоя, тем больше СГС вершины колонны. На третьем месте скорость распространения упругих поперечных волн в песчаном слое V_s_песок. Остальные факторы не оказывают значимого влияния на СГС вершины колонны. На рисунке 11 приведена карта Парето для отклика ГС вершины колонны.

Рис. 11 - Карта Парето для отклика ГС вершины колонны

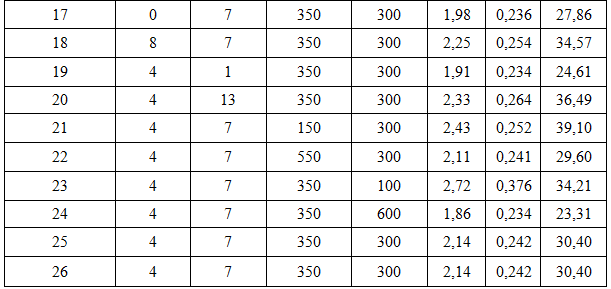
Таблица 1 - Матрица планирования численного эксперимента и значения откликов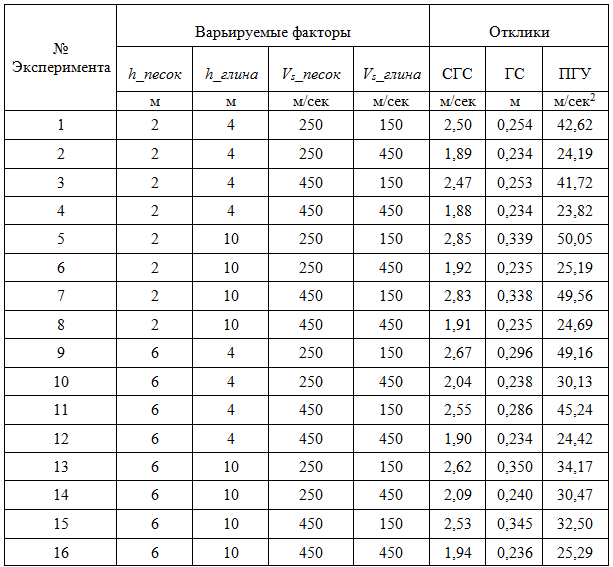

Наибольшее влияние оказывает V_s_глина со знаком минус. На втором месте мощность h_глина глинистого слоя со знаком плюс. На третьем месте стоит взаимодействие факторов h_глина и V_s_глина.

На рисунке 12 приведена карта Парето для отклика ПГУ вершины колонны. Все факторы оказались не значимы, за исключением фактора скорости распространения упругих поперечных волн в глинистом слое V_s_глина со знаком минус.

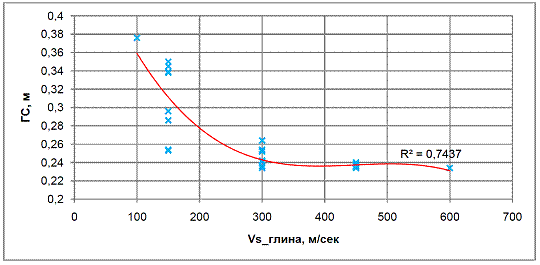
Был построен график зависимости ГС вершины колоны от скорости распространения упругих поперечных волн в глинистом прослое V_s_глина, данный график представлен на рисунке 13. Из графика видно, что данная зависимость носит нелинейный характер. При скоростях распространения упругих поперечных волн в глинистом прослое V_s_глина ниже 400 м/сек, смещения колонны возрастают. Величина достоверности аппроксимации R² составляет 0,7437.

Рис. 12 - Карта Парето для отклика ПГУ вершины колонны

Выполненные численные эксперименты по исследованию распространения сейсмической волны в слоистом основании наглядно показали особенности данного процесса, связанные с отражением волн от границ раздела грунтов и от свободной поверхности. В численных экспериментах показан эффект «ловушки», - сейсмическая волна, отражаясь от границы раздела грунтов, продолжает оставаться внутри слоя грунта, и

Рис. 13 - График зависимости ГС вершины колонны от V_s_глина глинистого слоя

 

становится источником сейсмических колебаний, увеличивая их продолжительность и изменяя характеристики. Полученные результаты помогают понять причины возникновения динамического усиления амплитуд колебаний на поверхности, а так же изменения частотных характеристик сейсмического воздействия и их продолжительности. Интерпретируемые результаты подтверждают изменение динамической нагрузки при условии наличия в основании выше коренных пород грунтов с более низкими значениями распространения скоростей упругих поперечных волн.

Многофакторный анализ для трехслойной модели грунтовой колонны, состоящей из коренных пород, слоя глины и поверхностного песчаного слоя выявил увеличение величин горизонтальных смещений, скоростей горизонтальных смещений и пиковых горизонтальных ускорений на вершине колонны со снижением значения распространения упругих поперечных волн в глинистом слое. Увеличение мощности глинистого слоя, так же приводит к увеличению откликов данных динамических параметров. В численных экспериментах многофакторного анализа не учитывалось влияние дополнительного динамического затухания, например полного затухания Релея или гистерезисного, так же в учет не принималось положение грунтовых вод и рельеф залегающих слоев грунта или поверхности. Все эти факторы являются предметом дальнейших исследований.

Обобщающим выводом проведенных исследований является рекомендация о необходимости индивидуального подхода к изучению динамических откликов площадок строительства, а так же в проведении исследований по выявлению наиболее важных факторов и их взаимодействия влияющих  на сейсмический эффект на поверхности. Многофакторный анализ позволяет понять, на что стоит обратить внимание при проектировании объектов и оценке их сейсмической устойчивости. В статье продемонстрировано возможность использования численных методов с подключением аппарата математической теории планирования экспериментов для решения данной задачи.

Литература

1. Вознесенский Е.А. Динамическая неустойчивость грунтов // Вестник Московского университета. Сер. геология. - 1995. - №5. - C.7I-88.
2. Cloud W. K. Intensity map and structural damage, Parkfield, California, Earthquake of June 27. 1966 // Bulletin of the Seismological society of America. 1967. V. 57. № 6. P. 1161-1179.
3. Rosenblueth E. The earthquake of 28 July 1957 in Mexico City // Proceedings 2nd World Conference on Earthquake Engineering, Japan. 1960. V. L.
4. FLAC 7.0 User manual. Dynamic analysis. Shear wave propagation in a vertical column. Itasca Consulting Group Inc. Minnesota. USA. 2011. P. 17-19.
5. Поляков С.В. Сейсмостойкие конструкции зданий: Учебное пособие для вузов. - 2-е изд. - М.: Высш. школа, - 1983. - 304 с.
6. Дэниел К. Применение статистики в промышленном эксперименте. Перевод с англ. [под ред. к.т.н. Э.К. Лецкого]. Изд-во «Мир», - М. - 1979. - 294 с.;
7. Джонсон Н., Лион Ф. Статистика и планирование эксперимента в технике и науке: Методы планирования эксперимента. Пер. с англ. - М.: Мир, - - 520 с.
8. Bernard R. Wair, Jason T. DeJong, Thomas Shantz. Guidelines for Estimation of Shear Wave Velocity Profiles, PEER Report 2012/08 // Pacific Earthquake Engineering Research Center. California, USA. 2012.

References

1. Voznesenskij E.A. Dinamicheskaja neustojchivost' gruntov // Vestnik Moskovskogo universiteta. Ser. geologija. - 1995. - №5. - C.7I-88.
2. Cloud W. K. Intensity map and structural damage, Parkfield, California, Earthquake of June 27. 1966 // Bulletin of the Seismological society of America. 1967. V. 57. № 6. P. 1161-1179.
3. Rosenblueth E. The earthquake of 28 July 1957 in Mexico City // Proceedings 2nd World Conference on Earthquake Engineering, Japan. 1960. V. L.
4. FLAC 7.0 User manual. Dynamic analysis. Shear wave propagation in a vertical column. Itasca Consulting Group Inc. Minnesota. USA. 2011. P. 17-19.
5. Poljakov S.V. Sejsmostojkie konstrukcii zdanij: Uchebnoe posobie dlja vuzov. - 2-e izd. - M.: Vyssh. shkola, - 1983. - 304 s.
6. Djeniel K. Primenenie statistiki v promyshlennom jeksperimente. Perevod s angl. [pod red. k.t.n. Je.K. Leckogo]. Izd-vo «Mir», - M. - 1979. - 294 s.;
7. Dzhonson N., Lion F. Statistika i planirovanie jeksperimenta v tehnike i nauke: Metody planirovanija jeksperimenta. Per. s angl. - M.: Mir, - 1981. - 520 s.
8. Bernard R. Wair, Jason T. DeJong, Thomas Shantz. Guidelines for Estimation of Shear Wave Velocity Profiles, PEER Report 2012/08 // Pacific Earthquake Engineering Research Center. California, USA. 2012.