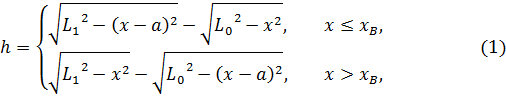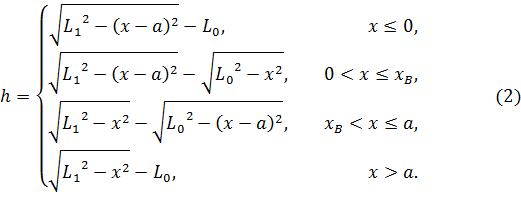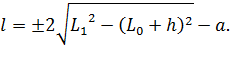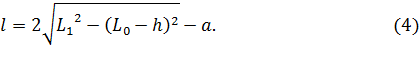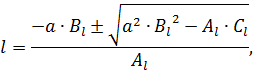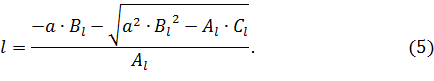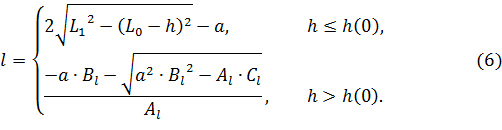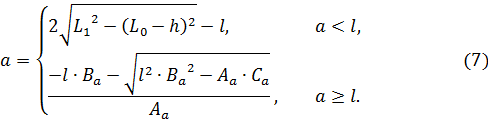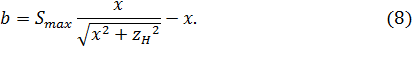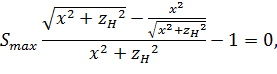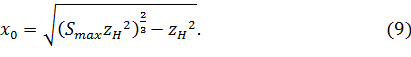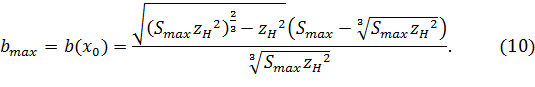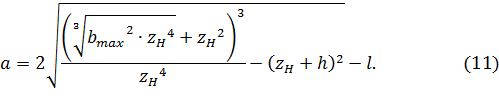ИССЛЕДОВАНИЕ ПАРАМЕТРОВ ОБСЛУЖИВАЕМОЙ ЗОНЫ РОБОТА ПАРАЛЛЕЛЬНОЙ СТРУКТУРЫ

Жавнер В.Л.¹, Никитина К.В.²

¹Доктор технических наук, профессор, Санкт-Петербургский политехнический университет Петра Великого; ²ORCID: 0000-0001-7557-2554, Аспирант

ИССЛЕДОВАНИЕ ПАРАМЕТРОВ ОБСЛУЖИВАЕМОЙ ЗОНЫ РОБОТА ПАРАЛЛЕЛЬНОЙ СТРУКТУРЫ

Аннотация

В работе рассматривается робот с параллельной кинематикой для погрузочно-разгрузочных работ. Выводятся зависимости длины и высоты обслуживаемой роботом зоны от положения рабочего органа, а также зависимость длины обслуживаемой зоны от ее высоты. Также в работе решается задача определения расстояния между креплениями приводных элементов по заданным значениям длины и высоты обслуживаемой зоны. Моделируется случай ограничения свободного пространства над роботом: производится расчет максимального расстояния до ограничения и, наоборот, по заданному расстоянию до ограничения вычисляется необходимое расстояние  между крепления приводных элементов.

Ключевые слова: Параллельный робот, обслуживаемая зона, погрузочно-разгрузочные работы.

Zhavner V.L.¹, Nikitina K.V.²

¹PhD in Engineering, Professor, Peter the Great Saint-Petersburg Polytechnic University; ²ORCID: 0000-0001-7557-2554, Postgraduate student

RESEARCH OF PARAMETERS OF THE SERVICE AREA OF ROBOT WITH PARALLEL STRUCTURE

Abstract

The paper deals with a parallel kinematics robot for loading and unloading. We derive the dependence of length and height of the area served by the robot from the position of working body and dependence of length of the service area from its height. Also in the paper we solve the problem of determining the distance between bindings of driving elements from the given values of length and height of the service area. It is modeled a case of restriction on the free space over the robot: there are calculated maximum distance to the restriction, and conversely, for a given distance to the limitations there are calculated the required distance between the mounting of driving elements.  

Keywords: parallel robot, service area, loading and unloading works.

На сегодняшний день роботы с параллельной кинематикой (в англоязычной литературе именуемые “parallel robots” – параллельные роботы) стали достаточно широко применяться в промышленности. Обладающие высоким быстродействием дельта-роботы уже зарекомендовали себя при обслуживании непрерывных технологических линий, например, при сортировке небольших изделий, переориентации изделий в потоке, сварке, размещении компонентов на печатных платах, а также в  фармацевтической и пищевой промышленности. Кроме дельта-роботов, разрабатываются новые фрезерные станки [4] с рабочим органом, перемещаемым механизмом параллельной структуры (триподом). В связи с этим, для параллельных роботов очень актуально расширение сфер применения, в частности, внедрение их на вспомогательные операции, такие как погрузочно-разгрузочные работы.

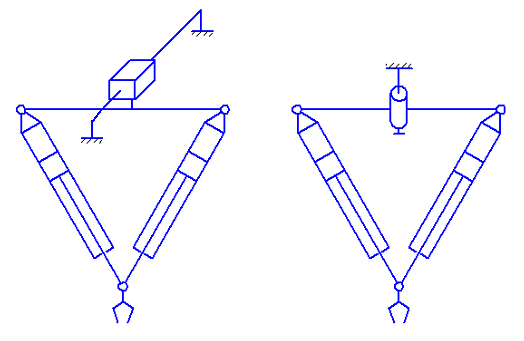
Для этих целей разработан робот с параллельной структурой с тремя степенями подвижности (рисунок 1). Необходимость в создании нового робота обусловлена тем, что большинство существующих параллельных роботов обладают избыточным для простых операций количеством степеней подвижности, а также недостаточной грузоподъемностью для переноса тары с изделиями, масса которой может достигать 50 кг. Робот, изображенный на рисунке 1, представляет собой в базовой плоскости шарнирную ферму переменной конфигурации [1], образованную двумя поступательными парами, закрепленную на третьей поступательной паре или на вращательной паре в зависимости от выполняемой операции. Стоит отметить, что данная схема очень эффективна при использовании гидроцилиндров, так как в этом случае значительно увеличивается грузоподъемность робота. Кроме того, таким роботом достаточно просто управлять. Общие принципы организации системы управления таким роботом изложены в работе [2].

Рисунок 1 – Структурная схема параллельного погрузочно-разгрузочного робота

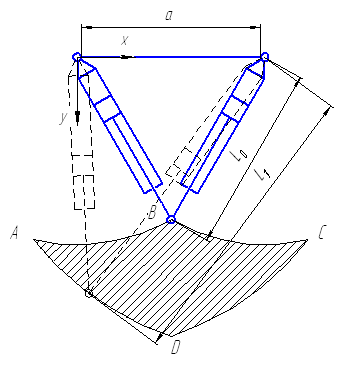
Одной из наиболее важных характеристик робота является обслуживаемая им зона (рисунок 2). В работе [3] показано, что для разработанного робота обслуживаемая зона в базовой плоскости представляет собой фигуру, образованную пересечением четырех окружностей с центрами на осях крепления приводных элементов (т.е. поступательных пар). Исследование обслуживаемой зоны сводилось к аналитическому представлению и определению координат граничных точек сечения зоны в базовой плоскости робота. Однако этого не достаточно для полноценного представления возможностей робота. Более информативными параметрами обслуживаемой зоны являются ее длина и высота, а также интерес представляет зависимость их друг от друга. Обычно для погрузочно-разгрузочных работ высота обслуживаемой зоны превышает ее длину. Это связано с тем, что робот укладывает готовую продукцию, снятую с конвейера, на поддон, который установлен на полу рабочего помещения в непосредственной близости с конвейером. В нашем случае используется обратный подход: длина больше высоты обслуживаемой зоны. Такой подход исключает подъем и опускание рабочего органа на длинные дистанции во время выполнения операции; для этих целей предусматривается специальная грузоподъемная платформа, которая обеспечивает установку коробок с продукцией на поддон на уровне конвейера.

Рисунок 2 – Сечение обслуживаемой зоны в базовой плоскости

Для нахождения максимально возможных размеров длины и высоты, которые можно вписать в фигуру (рисунок 2),  полученную при условии применения в конструкции робота одинаковых приводов, будем использовать известные из работы [3] уравнения окружностей, образующих обслуживаемую зону. Исходя из этого, высоту обслуживаемой зоны задаем как разницу между координатами точек соответствующих окружностей по оси ординат при одном и том же значении  x:

где  высота обслуживаемой зоны;

      текущее положение рабочего органа;

      расстояние между креплениями приводных элементов;

      минимальная длина приводного элемента;

       максимальный размер приводного элемента.

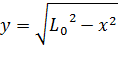Однако, в точках   и  имеем минимум функций  и 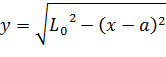 , равный . Ввиду невозможности вписать прямоугольник выше прямой  для точек, лежащих левее  и правее , полученную выше зависимость (1) высоты обслуживаемой зоны от координаты рабочего органа необходимо скорректировать:

Зависимость длины обслуживаемой зоны от координаты рабочего органа представлена ниже:

Изменение направления графика этой функции происходит в точке .

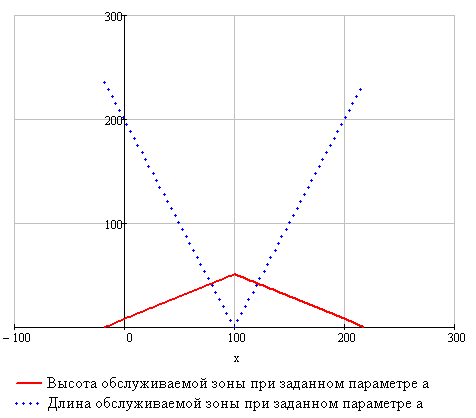
На рисунке 3 представлены графики зависимостей высоты и длины обслуживаемой зоны при определенном параметре , одинаковом для обеих зависимостей.

Рисунок 3 – Зависимость максимальных длины и высоты обслуживаемой зоны робота от положения рабочего органа

Из зависимостей (2) и (3) вытекает очевидный вывод: наибольшая длина обслуживаемой зоны достигается при нулевой ее высоте, и наоборот, наибольшая высота возможна только при нулевой длине обслуживаемой зоны робота. Кроме того, в силу использования идентичных приводов, полученные зависимости имеют симметричный характер – ось симметрии проходит через середину расстояния между креплениями приводных элементов.

Полученные графики дают наглядное представление о максимальных значениях параметров обслуживаемой зоны робота, но нас в большей степени интересует зависимость их друг от друга. Так как обе зависимости симметричны, будем рассматривать только левую часть графиков, т.е. область . На этом интервале высота зоны меняется в пределах , а длина – в пределах  .

Из представленной выше системы уравнений (2) для нахождения высоты обслуживаемой зоны берем первые два уравнения и выражаем длину зоны. Для выбранного интервала координата рабочего органа в соответствии с (3) равна . Легко показать, что корни первого уравнения системы (2) имеют следующий вид:

Так как нас интересует только тот корень, который удовлетворяет условию , получаем, что на отрезке  длина равна:

Корни второго уравнения системы (2) можно записать следующим образом:

где соответствующие коэффициенты имеют вид:

Нас интересует тот корень, который удовлетворяет условию . В этом случае получаем, что на отрезке  длина равна:

Объединяя найденные решения (4) и (5), запишем итоговую формулу для нахождения зависимости длины обслуживаемой зоны от ее высоты:

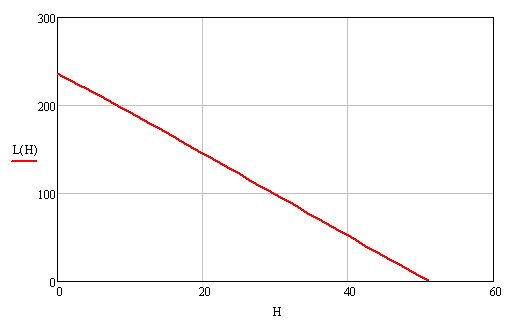
На рисунке 5 изображен график зависимости (6) длины зоны от ее высоты. Из графика видно, как меняется максимально возможная длина при изменении высоты обслуживаемой зоны от нуля до максимума. В данном случае происходит изгиб при , т.е. в этой точке наблюдается переход с одного решения на другое. Следует отметить, что полученная кривая является верхней границей, а под графиком расположено множество всех возможных размеров длины и высоты обслуживаемой зоны робота.

Рисунок 5 – Зависимость длины обслуживаемой зоны от её высоты

Для решения обратной задачи, т.е. для нахождения параметра , необходимо решить систему первых двух уравнений из системы (2) относительно неизвестной . После проведенных вычислений получаем итоговую формулу для нахождения расстояния между осями закрепления приводов от размеров обслуживаемой зоны:

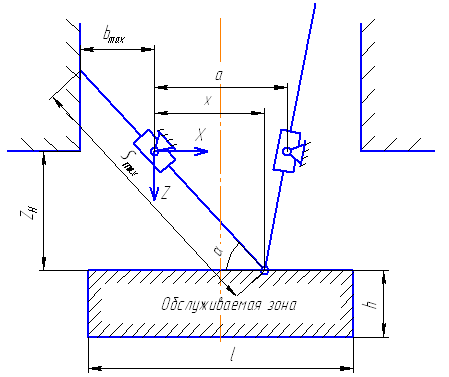
Все предыдущие расчеты проводились для случая, когда рабочий объем робота не ограничен сверху и свободные концы поступательных пар могут беспрепятственно совершать любые перемещения. Однако в производственных помещениях часто бывает так, что пространство над роботом в силу различных причин имеет вполне определенные границы, как показано на рисунке 6.

Рисунок 6 – Расчетная схема для определения ограничений обслуживаемой зоны робота

Поэтому дальнейший геометрический синтез сводится к оценке наибольшего размера , который достигается при движении рабочего органа по верхней границе обслуживаемой зоны. Из рисунка 6 видим, что

Нетрудно заметить, что наибольшее расстояние до ограничения можно представить в виде:

Для того чтобы оценить максимальное значение размера , необходимо взять производную от (8) и приравнять ее к нулю.

При найденном положении  рабочего органа размер  является максимальным. Подставив значение (9) в уравнение (8), получим, чему равно максимальное значение :

Обратная задача сводится к тому, чтобы найти зависимость параметра  между осями закрепления приводов от расстояния  при условии, что  заранее известно.

Используя замену  и подставляя в полученную зависимость (10) значение  вычислим искомый параметр :

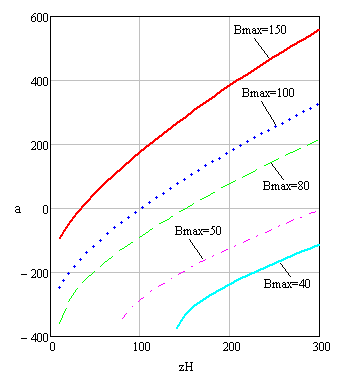
Графики зависимости  при различных значениях  представлены на рисунке 7. Очевидно, что размер  не может быть меньше нуля, поэтому кривые, построенные при  и  не учитываем, они приведены для наглядности.

Рисунок 7 – Зависимость расстояния a между осями закрепления 

приводных элементов от расстояния На основании представленных в работе расчетов можно оценить по исходным размерам выбранных приводных элементов и расстояния между ними максимально возможные размеры обслуживаемой зоны разработанного робота и выбрать в соответствии с поставленной задачей конкретные значения длины и высоты обслуживаемой зоны. В то же время, исходя из размеров требуемой для выполнения некоторой технологической операции обслуживаемой зоны, можно подобрать такую конфигурацию робота, которая будет наиболее удовлетворять поставленным требованиям.

Литература

1. Жавнер В.Л. Роботы и манипуляторы для погрузочно-разгрузочных работ: дис. … докт. техн. наук / В.Л. Жавнер. – Санкт-Петербург, 1992. – 535 с.
2. Жавнер В.Л. Система управления манипулятором / В.Л. Жавнер, К.В. Никитина // Научный форум с международным участием «Неделя науки СПбПУ»: материалы научно-практической конференции. Институт металлургии, машиностроения и транспорта. Ч. 2. – Санкт-Петербург, 2015. – С. 10-13.
3. Никитина К.В. Обслуживаемая зона параллельных манипуляторов / К.В. Никитина, В.Л. Жавнер // Неделя науки СПбПУ: материалы научного форума с международным участием. Институт металлургии, машиностроения и транспорта. Ч. 1. – Санкт-Петербург, 2015. – С. 18-20.
4. Панов С.С. Фрезерный станок с параллельной кинематикой / С.С. Панов, О.Н. Густова, П.Г. Мазеин // Известия Самарского научного центра Российской академии наук. – 2012. – №1-2(14). – С. 419-421.

References

1. Zhavner V.L. Roboty i manipuljatory dlja pogruzochno-razgruzochnyh rabot: dis. … dokt. tehn. nauk / V.L. Zhavner. – Sankt-Peterburg, 1992. – 535 s.
2. Zhavner V.L. Sistema upravlenija manipuljatorom / V.L. Zhavner, K.V. Nikitina // Nauchnyj forum s mezhdunarodnym uchastiem «Nedelja nauki SPbPU»: materialy nauchno-prakticheskoj konferencii. Institut metallurgii, mashinostroenija i transporta. Ch. 2. – Sankt-Peterburg, 2015. – S. 10-13.
3. Nikitina K.V. Obsluzhivaemaja zona parallel'nyh manipuljatorov / K.V. Nikitina, V.L. Zhavner // Nedelja nauki SPbPU: materialy nauchnogo foruma s mezhdunarodnym uchastiem. Institut metallurgii, mashinostroenija i transporta. Ch. 1. – Sankt-Peterburg, 2015. – 18-20.
4. Panov S.S. Frezernyj stanok s parallel'noj kinematikoj / S.S. Panov, O.N. Gustova, P.G. Mazein // Izvestija Samarskogo nauchnogo centra Rossijskoj akademii nauk. – 2012. – №1-2(14). – S. 419-421.