МОДЕЛИРОВАНИЕ ФИНАНСОВЫХ ВРЕМЕННЫХ РЯДОВ НА ОСНОВЕ ПРОЦЕССОВ ЛЕВИ ДЛЯ ОПРЕДЕЛЕНИЯ ПРЕМИИ ОПЦИОННЫХ КОНТРАКТОВ

МОДЕЛИРОВАНИЕ ФИНАНСОВЫХ ВРЕМЕННЫХ РЯДОВ НА ОСНОВЕ ПРОЦЕССОВ ЛЕВИ ДЛЯ ОПРЕДЕЛЕНИЯ ПРЕМИИ ОПЦИОННЫХ КОНТРАКТОВ

Научная статья

Ефремов В.А.

Томский государственный университет систем управления и радиоэлектроники, Томск, Россия

Аннотация

Рассмотрены основные подходы к ценообразованию опционов. Предложена адаптивная модель описания динамики цен базовых активов. Проведен сравнительный анализ полученной модели с известными на эмпирических данных цен индекса РТС.

Ключевые слова: деривативы, риск, процессы Леви, модели ценообразования опционов.

Key words: derivatives, risk, Levy processes, options valuation.

Современная развитая рыночная экономика любой страны не может существовать без эффективного финансового рынка, где особое место занимает срочный рынок. В рамках срочного рынка осуществляется не только перераспределение денежных средств между его участниками, но и хеджирование рисков. В условиях бурно растущего финансового рынка его участники все чаще и чаще заключают сделки с производными финансовыми инструментами (деривативы).

Производный финансовый инструмент, как экономическое явление – это отношение, вытекающее из соглашения участников, направленное на осуществление любой из функций производных, основанное на асимметрии прав и обязательств, двух участников сделки [1]. В настоящее время срочный рынок существенно превосходят фондовый по объему торгов. Данный факт обуславливается тем, что производные ценные бумаги являются наиболее гибкими инструментами на финансовом рынке, поскольку позволяют участникам рынка более эффективно реагировать на происходящие перемены.

Российский рынок производных финансовых инструментов в последние годы динамично растет, однако его объемы существенно ниже, чем в других развитых странах (США, Германия, Великобритания и др.). Наиболее распространенными видами деривативов на российском рынке являются фьючерсы и опционы. Опцион является более сложным финансовым инструментом, нежели фьючерс. В первую очередь это связано с тем, что любой опцион имеет свою стоимость (премию). Определение «справедливой» стоимости опционного контракта – ключевая задача любого участника рынка опционов. В экономическом смысле премия опциона – это плата за риск неблагоприятного изменения цены базового актива, который берет на себя продавец.

Основы ценообразование опционных контрактов

В условиях неэффективности современного рынка возникает понятие справедливой стоимости опционного контракта, что соответствует принципу отсутствия арбитража [2]. В свою же очередь, модель рынка безарбитражна тогда и только тогда, когда существует мартингальная (риск-нейтральная) мера Q, такая что выполняется следующее условие [3]:

где S₀– это текущая цена базового актива, r– безрисковая процентная ставка и S_t – цена актива в момент времени t.

Поиск такой мартингальной меры Q, в которой вероятностное пространство, моделирующее изменение цен базовых активов, есть мартингал, является основной и наиболее сложной задачей при определении справедливой стоимости опционов. Такой подход к ценообразованию опционов называется риск-нейтральным. В риск-нейтральном вероятностном пространстве средние будущие значения цен активов не зависят от риска, а так же совпадают с текущими значениями, то есть цены активов в таком пространстве, дисконтированные по безрисковой процентной ставке, является мартингалами. При известной мартингальной мере Q справедливая стоимость ванильного (европейского) опциона колл определяется следующим образом [4]:

где C– это цена европейского опциона колл; r – безрисковая процентная ставка; T – дата истечения срока опциона;  S_T – цена базового актива в момент времени T; K – цена исполнения опционного контракта (страйк).

Предположение о том, что изменение цены базового актива является броуновским движением не противоречит риск-нейтральному подходу к ценообразованию опционов, так как такой стохастический процесс есть мартингал. Однако, несмотря на то, что данное предположение является спорным, эта модель применяется практически на всех биржевых и внебиржевых площадках в силу того, что она имеет простую аналитическую форму [5]:

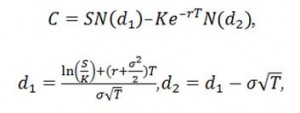
где C – цена опциона колл; S – текущая цена базового актива; K – цена исполнения опционного контракта (страйк); r – безрисковая процентная ставка; σ – подразумеваемая волатильность; N(x) – функция нормального распределения со среднем в нуле и стандартным отклонением равным единице; T – время до истечения срока опциона.

Информация имеет разную значимость для участников срочного рынка и влияет на динамику цен базовых активов абсолютно по-разному. Наряду с информацией, которая незначительно влияет на доходность базовых активов, присутствует информация, существенным образом влияющая как на отдельно взятый актив, так и на рынок в целом. К такой информации можно отнести экономический кризис, дефолт компании, землетрясение и т.д. Процессы Леви позволяют моделировать динамику цен активов максимально гибко, так как содержат две составляющие: броуновское движение (диффузия процесса) и скачкообразный компонент.

В настоящее время существует множество моделей, основанных на процессах Леви, которые успешно моделируют динамику цен различных активов и используются при ценообразовании опционов, так как являются мартингалами.

Пусть {X_t|≥0} – стохастический процесс, определенный на пространстве с фильтрацией F={f_t|t≥0}. Предполагается, что X – это процесс Леви относительно фильтрации F, X является неограниченным слева, где X_u-X_t не зависит от f_t и имеет следующую характеристическую функцию (теорема Леви-Хинчина):

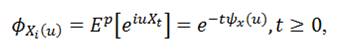
где характеристическая экспонента ψ_x(u) выражается следующим образом:

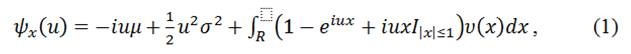
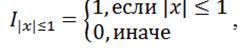
где μ описывает постоянный дрейф, σ² определяет постоянную дисперсию непрерывной компоненты процесса Леви и мера Леви описывает плотность распределения скачков. Тройка (μ,σ²,υ(x)) полностью определяет такой процесс и называется триплетом Леви [6]. Как правило, ценообразование опционов и вероятностная оценка процессов Леви основываются на подборке такого триплета, который наилучшим образом описывает эмпирическую динамику цен базового актива.

Декомпозиция Леви-Ито (2) разбивает процессы Леви на простые составляющие и помогает понять их природу.

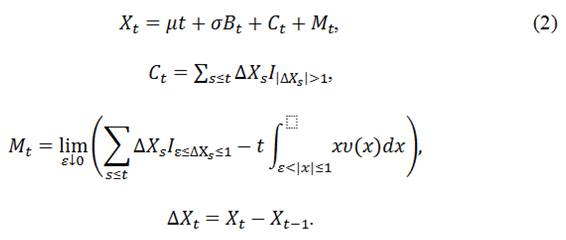
где B_t – это Броуновская компонента; C_t– это составной процесс Пуассона с интенсивностью скачков λ и плотностью распределения размера скачков υ(x); M_t – это мартингал с очень маленькими скачками (компенсационный тренд).

Такая декомпозиция является основой для моделирования процессов Леви при помощи суммы двух составляющих: Броуновского движения и составного процесса Пуассона. Такая структура стохастического процесса называется скачкообразной диффузией и имеет вид:

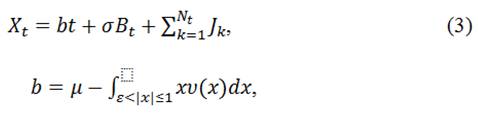
где N_t – процесс Пуассона с интенсивностью λ и J_k – случайный скачок с размером, имеющий плотность распределения .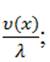

Моделирование финансовых временных рядов на основе процессов Леви

Любой базовый актив имеет свою собственную динамику, на определенном временном интервале. Связанно это с тем, что рынок становится все более и более рискованным. В таких условиях применение одной из известных моделей для описания доходностей активов без изменений ее параметров, является невозможным. Иногда модель может быть адаптирована путем изменения ее параметров, а иногда она и вовсе становится не применимой в таких условиях.

Анализ российского фондового рынка показал, что логарифмическая доходность большинства активов не подчиняется закону нормального распределения. Так, например, логарифм доходностей фьючерса на индекс РТС в период с 03.08.2005 по 05.06.2006 (Рис.1) имеет распределение отличное от нормального. Оценка такой выборки критерием согласия Пирсона (χ²=63.78) показывает, что данная выборка не может быть аппроксимирована нормальным распределением, которое используется в настоящее время для оценки справедливой стоимости опционов.

 

 

 

 

 

 

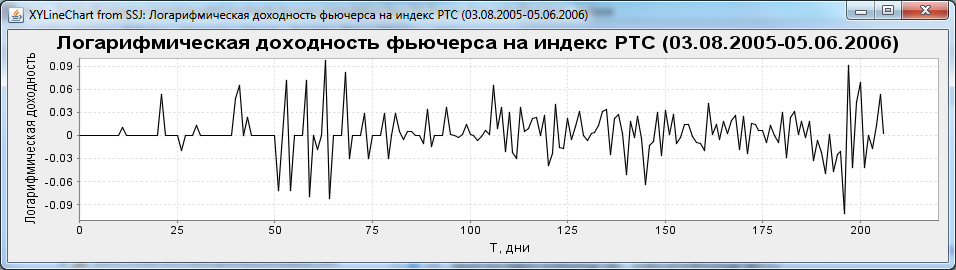
Рис.1. Логарифмическая доходность на индекс РТС в период с 03.08.2005 по 05.06.2006

В своей диссертации «Моделирование и анализ эффективности ценообразования опционов на российском срочном рынке» Морозова М.М. предложила методику калибровки известных моделей к эмпирическим данным и показала эффективность применения такой методики к российскому фондовому рынку [7]. Такой процесс является трудоемким и требующий участия опытного финансового инженера, который сводится к подбору триплета Леви и его параметров.

Автором статьи предложен автоматизированный подход к определению триплета Леви, исходя из ретроспективных данных по доходностям моделируемого базового актива. В основе такого подхода лежит предположение о том, что цена актива меняется диффузно со скачками, которые возникают в связи с важной информацией, поступающей случайно. Поток такого рода информации является составным процессом Пуассона с плотностью распределения размера скачков υ(x). Для определения υ(x) и других характеристик процесса Леви использовался следующий алгоритм:

1. Проверка эмпирических данных критерием согласия Пирсона на гипотезу о том, что ретроспективная логарифмическая доходность имеет нормальный закон распределения.
2. Определение эмпирической волатильности σ_e и тренда μ_e для подбора параметров нормального распределения, которое будет описывать Броуновскую составляющую процесса Леви (3). Если эмпирическая логарифмическая доходность имеет нормальный закон распределения, то получаем диффузную модель c параметрами (μ_e,σ_e), иначе переходим к шагу 3.
3. Определение скачков. На данном этапе отбрасывается диффузионная составляющая ретроспективной логарифмической доходности и определяется последовательность скачков.
4. На заключительном этапе строится непараметрическая оценка Розенблатта-Парзена плотности вероятности полученных скачков вида:

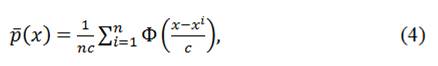
где Φ(x) – ядерная функция, n – количество измерений, c – ширина интервала построенной гистограммы и xⁱ – результат -го измерения. В данном алгоритме используется ядерная функция Епанечникова.

Результатом работы алгоритма построения модели скачкообразной диффузии на основе эмпирических данных является триплет Леви 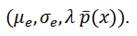 Таким образом, полученная стохастическая модель логарифмической доходности базового актива имеет следующий вид (5):

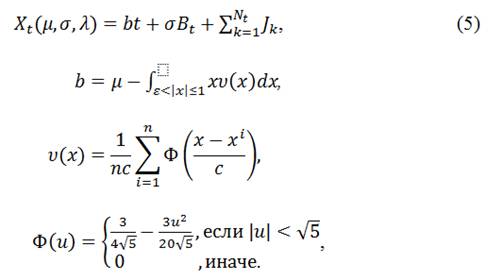
где N_t – процесс Пуассона с интенсивностью λ (интенсивность появления скачков); J_k– случайный скачок с размером, имеющий плотность распределения 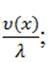; n – количество измерений и xⁱ– результат -го измерения; c – ширина интервала построенной гистограммы.

Цена же базового актива определяется как геометрическая модель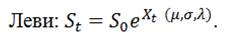  

Апробация результатов программного комплекса, который реализует данную модель (5), проводилась на основе исторических данных индекса РТС и фьючерса на индекс РТС, показала свою состоятельность и адаптивность.

Результаты моделирования (Рис.2) динамики цен фьючерсного контракта на индекс РТС в период с 03.08.2005 по 05.06.2006 говорят о том, что для данной эмпирической выборки χ²=1.903, следовательно эмпирические данные не противоречат закону распределения полученной модели с доверительным интервалом равным 95%. Параметры модели: μ=0.03, σ=0.336 и λ=0.9.

Анализ той же выборки, проведенный Морозовой М.М. в своем диссертационном исследовании, обосновал применение обратного Гауссовского процесса (NIG) с параметрами [7]: μ=-0.0005, σ²=0.0017 и k=6.6777, что подтверждается экспериментами и значением χ²=4.67 с 7 степенями свободы, а так же доверительным интервалом 70%.

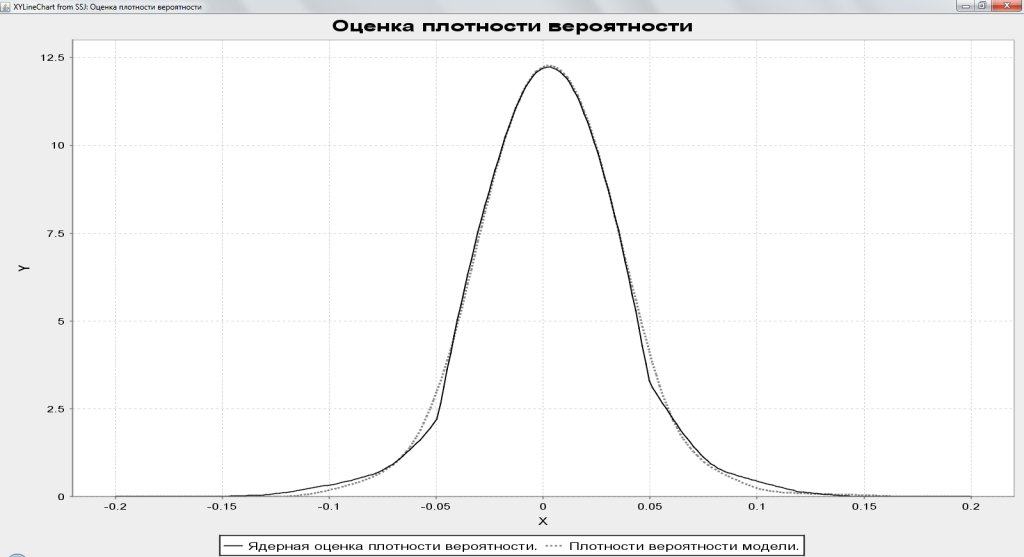
Рис.2. Результаты моделирования динамики цен фьючерсного контракта на индекс РТС в период с 03.08.2005 по 05.06.2006

Выводы

Переходный характер российской экономики, ее высокие риски при дефиците инвестиций и проблемном финансовом секторе обосновывают необходимость в создании новых моделей динамики цен на фондовом рынке. Такие модели должны быстро реагировать на рыночные изменения, именно поэтому большинство современных моделей имеют большое количество параметров, что усложняет их практическое применение. Каждая известная модель имеет свои ограничение и не может быть применена для описания всех без исключения активов.

Предложенная и реализованная автором модель (5) позволяет успешно моделировать динамику цен на индекс РТС, используя процессы Леви, эффективнее, чем известные модели. Достоинствами этой модели являются:

• высокая точность прогноза логарифмической доходности цен на фондовом рынке;
• адаптивность модели к различным ситуациям на фондовом рынке;
• независимость модели от ретроспективной динамики цен на базовые активы;
• возможность использования модели для определения справедливой цены опционов.

К недостаткам модели можно отнести:

• необходимость в ретроспективных данных, моделируемого базового актива;
• отсутствие аналитического вида характеристической функции;
• модель может описывать только стохастические процессы со скачкообразной диффузией.

Представленная модель (5) хорошо описывает распределения с толстыми хвостами и различной асимметрией, так как использует ретроспективные данные как один из параметров.

Список литературы / References

1. Фельдман А.Б. Производные финансовые и товарные инструменты – М. Экономика, 2008. – 486 с.
2. Bingham N. H., Kiesel R. Risk-Neutral Valuation. Pricing and Hedging Of Financial Derivatives. – London: Springer, 2004. – P. 105-142.
3. Бьорк Т. Теория арбитража в непрерывном времени / Перевод с англ. Я. И. Белопольский. – М.: МЦНМО, 2010. – 560 с.
4. Schoutens W. Exotic Options under Levy Models: An Overview / Belgium, 2004. – P. 4-6.
5. Black F., Scholes M. The Pricing of Options and Corporate Liabilities / The Journal of Political Economy, 1973. – V. 81. – № 3 (May). – P. 637–654.
6. Wu L. Modeling Financial Security Returns Using Levy Processes / Zicklin School of Business, Baruch College, City University of New York, 2008. – V.15. − P. 1−56.
7. Морозова М.М. Моделирование и анализ эффективности ценообразования опционов на российском рынке: дисс. канд. экон. наук / Институт экономики и организации промышленного производства Сибирского отделения Российской академии наук. – Новосибирск, 2010. – С.172–182.

 

Опубликовать статью