К ПРОБЛЕМЕ ОПРЕДЕЛЕНИЯ АКТУАЛЬНЫХ ПАРАМЕТРОВ ВЫСОКОВОЛЬТНЫХ ВОЗДУШНЫХ ЛИНИЙ ЭЛЕКТРОПЕРЕДАЧИ
К ПРОБЛЕМЕ ОПРЕДЕЛЕНИЯ АКТУАЛЬНЫХ ПАРАМЕТРОВ ВЫСОКОВОЛЬТНЫХ ВОЗДУШНЫХ ЛИНИЙ ЭЛЕКТРОПЕРЕДАЧИ
Научная статья
Иванов И.Е.
Ивановский государственный энергетический университет имени В.И. Ленина, Иваново, Россия
Аннотация
Рассмотрена проблема изменения продольных параметров воздушных линий электропередачи в контексте обеспечения правильного функционирования устройств релейной защиты и автоматики данных линий. Приведены результаты численного моделирования в программном комплексе MATLAB, свидетельствующие о существенной вариации активных и индуктивных сопротивлений линий электропередачи в зависимости от ряда факторов.
Ключевые слова: актуальные параметры линий электропередачи, сопротивление прямой последовательности, сопротивление нулевой последовательности, интеграл Карсона.
Key words: transmission line actual parameters, positive sequence impedance, zero sequence impedance,Carson’s integral.
Параметры воздушных линий электропередачи (ВЛЭП) используются алгоритмами многих устройств релейной защиты и автоматики (УРЗА), поэтому их правильное определение необходимо для обеспечения корректного функционирования УРЗА. Классические подходы к определению продольных параметров ВЛЭП (активных и индуктивных сопротивлений) обычно оперируют некоторыми усреднёнными данными, которые предполагаются неизменными. К таким данным относятся геометрическое расположение проводников ВЛЭП друг относительно друга и поверхности земли, физические свойства фазных проводников и грунта (прежде всего, проводимость), а также типичные (или принимаемые таковыми) атмосферные условия. Полное собственное сопротивление проводника ВЛЭП можно разделить на три составляющих [1], одна из которых учитывает влияние земли как неидеальной проводящей поверхности. Данная составляющая, как правило, вычисляется с использованием интеграла Карсона [2, 3] и его различных аппроксимаций [4, 5] или по упрощенной методике, изложенной в [1]. Внутреннее сопротивление фазного провода вычисляется с применением функций Бесселя. Все эти алгоритмы используют указанную выше информацию относительно физических свойств системы и атмосферных условий, которая может не соответствовать действительности. Это особенно актуально в отношении ВЛЭП, расположенных в регионах со значительными сезонными изменениями погодных условий (например, большая часть территории Российской Федерации). Продольные параметры ВЛЭП необходимы для вычисления параметров срабатывания (уставок) некоторых УРЗА ВЛЭП. Следовательно, УРЗА могут функционировать некорректно (сработать ложно или излишне, либо неправильно определить расстояние до места повреждения), если их уставки не отражают реального состояния контролируемой ВЛЭП.
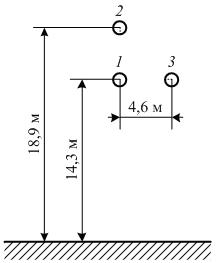
Одним из факторов, оказывающих существенное влияние на значение удельного продольного сопротивления ВЛЭП, является проводимость земли (грунта) вдоль трассы ВЛЭП. В [6] приведены результаты экспериментов, свидетельствующие о значительной вариации проводимости земли вследствие изменения объёмного содержания влаги. Рассмотрим трёхфазную ВЛЭП с геометрией, представленной на рис. 1, и следующими параметрами:
– удельное сопротивление фазных проводников постоянному току в расчёте на единицу длины ЛЭП: 0,109 Ом/км;
– радиус фазных проводников: 0,88∙10-2 м;
– удельное сопротивление грунта: 100 Ом∙м для первого эксперимента; 1000 Ом∙м для второго эксперимента.
Рис. 1. Геометрические параметры трёхфазной ВЛЭП, используемые для вычислительных экспериментов
Для получения матриц фазных параметров ВЛЭП в программном обеспечении MATLAB был разработан код (m-файл), позволяющий вычислять собственные и взаимные сопротивления проводников на основании вводимых данных, описывающих геометрическое расположение проводников и физические свойства системы. Для реализации интеграла Карсона был использован пакет Symbolic Math Toolbox. Корректность разработанного кода была подтверждена посредством сопоставления выдаваемых результатов с результатами, полученными в программном комплексе ATP (в частности, с помощью подпрограммы LCC). В табл. 1 представлены элементы двух матриц полных сопротивлений на единицу длины ЛЭП, полученных посредством двух вычислительных экспериментов. Очевидно, при увеличении удельного сопротивления грунта действительные части элементов изменяются незначительно, тогда как мнимые части подвержены существенной вариации.
Сравнение всех соответствующих элементов двух матриц было выполнено в программном комплексе MATLAB. В результате были получены следующие данные:
– максимальное увеличение собственной индуктивности: 9,57%;
– максимальное увеличение собственного полного сопротивления: 9,2%;
– максимальное увеличение взаимной индуктивности: 22,63%;
– максимальное увеличение взаимного полного сопротивления: 22,22%.
Таблица 1
Матрицы полных сопротивлений (Ом/км) трёхфазной ВЛЭП на частоте 50 Гц при различных значениях проводимости грунта
|
МАТРИЦА 1 |
||||
|
Сопротивление грунта: 100 Ом∙м |
Столбцы матрицы |
|||
|
1 |
2 |
3 |
||
|
Строки матрицы |
1 |
0,1575 + 0,7443j |
0,0475 + 0,3356j |
0,0478 + 0,3354j |
|
2 |
0,0475 + 0,3356j |
0,1570 + 0,7448j |
0,0475 + 0,3139j |
|
|
3 |
0,0478 + 0,3354j |
0,0475 + 0,3139j |
0,1575 + 0,7443j |
|
|
МАТРИЦА 2 |
||||
|
Сопротивление грунта: 1000 Ом∙м |
Столбцы матрицы |
|||
|
1 |
2 |
3 |
||
|
Строки матрицы |
1 |
0,1586 + 0,8155j |
0,0487 + 0,4067j |
0,0488 + 0,4066j |
|
2 |
0,0487 + 0,4067j |
0,1584 + 0,8157j |
0,0487 + 0,3849j |
|
|
3 |
0,0488 + 0,4066j |
0,0487 + 0,3849j |
0,1586 + 0,8155j |
|
Изменения сопротивлений в процентном выражении, приведённые выше, очень существенны. УРЗА обычно реагируют на составляющие отдельных последовательностей, поэтому интересно узнать, насколько при этом изменяются сопротивления прямой и нулевой последовательностей. Полагая, что рассматриваемая ВЛЭП является транспонированной, эти сопротивления можно вычислить следующим образом:
где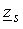 
– собственное сопротивление; 
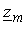– взаимное сопротивление; 
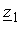– сопротивление прямой последовательности; 
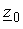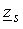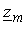– сопротивление нулевой последовательности. При этом элементы и являются средними арифметическими всех диагональных и недиагональных элементов соответственно. Применяя данный подход, были получены следующие результаты:
– сопротивление прямой последовательности (Ом/км) для матрицы 1: 0,1098 + 0,4162j;
– сопротивление прямой последовательности (Ом/км) для матрицы 2: 0,1098 + 0,4162j;
– видимые изменения в значении сопротивления прямой последовательности отсутствуют;
– сопротивление нулевой последовательности (Ом/км) для матрицы 1: 0,2526 + 1,4010j;
– сопротивление нулевой последовательности (Ом/км) для матрицы 2: 0,2561 + 1,6143j;
– увеличение индуктивности нулевой последовательности: 15,22%;
– увеличение полного сопротивления нулевой последовательности: 14,81%.
Полученные результаты свидетельствуют о существенном изменении сопротивления нулевой последовательности при изменении проводимости грунта вдоль трассы ВЛЭП, например, вследствие осадков или обильного снеготаяния. Поэтому УРЗА, реагирующие на компоненты нулевой последовательности (например, дистанционная защита от замыканий на землю, а также устройства определения расстояния до места повреждения), не смогут функционировать правильно без соответствующей корректировки уставок.
Рассмотрим теперь влияние изменений в значении сопротивлений фазных проводников. Известно, что электрическое сопротивление металлов изменяется в зависимости от температуры. Для численных вычислений обычно используют следующую линейную аппроксимацию:
где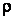 
– удельное сопротивление металла при температуре 
; 
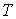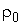– удельное сопротивление металла при температуре 
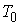(обычно при 20˚C); 
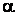– температурный коэффициент электрического сопротивления.
Большинство ВЛЭП высокого напряжения сооружаются с использованием сталеалюминиевых проводов, однако алюминиевые проводники (или изготовленные из сплавов алюминия) также имеются в эксплуатации. С целью некоторого упрощения задачи рассмотрим «чисто» алюминиевый проводник. Его параметры 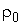и 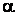приведены в справочных таблицах, например, в [7]: 
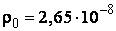Ом∙м при 20˚C; 
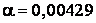1/˚C. Используя данные значения и выражение (3), можно вычислить сопротивление алюминия при 0˚C и 50˚C. Подобные температурные вариации вполне возможны на практике, и могут быть больше [8]. Применяя разработанный в MATLAB код, были получены две матрицы полных сопротивлений ВЛЭП (табл. 2). Вычисляя на основе данных, представленных в табл. 2, сопротивления прямой и нулевой последовательностей в соответствии с (1) и (2), получаем следующие результаты:
– сопротивление прямой последовательности (Ом/км) для матрицы 1: 0,1004 + 0,4162j;
– сопротивление прямой последовательности (Ом/км) для матрицы 2: 0,1236 + 0,4162j;
– увеличение активного сопротивления прямой последовательности: 23,14%;
– увеличение полного сопротивления прямой последовательности: 1,41%;
– сопротивление нулевой последовательности (Ом/км) для матрицы 1: 0.2432 + 1.4010j;
– сопротивление нулевой последовательности (Ом/км) для матрицы 2: 0.2665 + 1.4010j;
– увеличение активного сопротивления нулевой последовательности: 9,55%;
– увеличение полного сопротивления нулевой последовательности: 0,29%.
Таблица 2
Матрицы полных сопротивлений (Ом/км) трёхфазной ВЛЭП на частоте 50 Гц при различных значениях температуры фазных проводников
|
МАТРИЦА 1 |
||||
|
Температура: 0˚C |
Столбцы матрицы |
|||
|
1 |
2 |
3 |
||
|
Строки матрицы |
1 |
0,1482 + 0,7443j |
0,0475 + 0,3356j |
0,0478 + 0,3354j |
|
2 |
0,0475 + 0,3356j |
0,1477 + 0,7448j |
0,0475 + 0,3139j |
|
|
3 |
0,0478 + 0,3354j |
0,0475 + 0,3139j |
0,1482 + 0,7443j |
|
|
МАТРИЦА 2 |
||||
|
Температура: 50˚C |
Столбцы матрицы |
|||
|
1 |
2 |
3 |
||
|
Строки матрицы |
1 |
0,1714 + 0,7443j |
0,0475 + 0,3356j |
0,0478 + 0,3354j |
|
2 |
0,0475 + 0,3356j |
0,1709 + 0,7448j |
0,0475 + 0,3139j |
|
|
3 |
0,0478 + 0,3354j |
0,0475 + 0,3139j |
0,1714 + 0,7443j |
|
Анализируя полученные результаты, можно заключить, что продольное активное сопротивление ВЛЭП может существенно варьироваться в течение года. Несмотря на то, что полное сопротивление при этом не изменяется в такой степени, как при вариации проводимости грунта, очень важно контролировать актуальное значение активной составляющей. Дело в том, что для задания характеристик некоторых УРЗА, например, дистанционных реле, часто требуется знать активную и реактивную компоненты отдельно. На основании данной информации, в частности, рассчитывается характеристический угол линии. Очевидно, если не принимать во внимание изменения активного сопротивления в зависимости от температуры (табл. 2), он будет рассчитан неверно, поскольку индуктивное сопротивление при этом не изменяется.
Таким образом, сопротивление как прямой, так и нулевой последовательности ВЛЭП может варьироваться в широких пределах в зависимости от ряда факторов. Это обстоятельство оказывает существенное влияние на функционирование УРЗА ВЛЭП и, следовательно, всей электроэнергетической системы, что диктует необходимость разработки алгоритма определения актуальных параметров ВЛЭП и использования результатов его работы в современных микропроцессорных УРЗА.
Список литературы / References
1. Juan A. Martinez-Velasco, Power system transients: parameter determination, CRCPress,USA, 2009.
2. Abner Ramirez and Felipe Uribe, “A broad range algorithm for the evaluation of Carson’s integral”, IEEE Transactions on Power Delivery, Vol. 22, No. 2, April 2007, pp. 1188-1193.
3. F. Rachidi and S. Tkachenko, Electromagnetic Field Interaction with Transmission Lines – from Classical Theory to HF Radiation Effects, WIT Press, Great Britain, 2008.
4. H.W. Dommel, Electromagnetic Transients Program (EMTP) Theory Book, Bonneville Power Administration, 1986.
5. Руководящие указания по релейной защите. Вып. 11. Расчёты токов короткого замыкания для релейной защиты и системной автоматики в сетях 110-750 кВ. – М.: Энергия, 1979. – 152 с.
6. Тарасов, А. Гамма-съёмка. Новый метод оценки коррозионных свойств грунта на трассах ВЛ / Александр Тарасов, Василий Цилько // Новости электротехники. – 2005. – № 2(32).
7. Resistivity and Temperature Coefficient at 20 C[Электронный ресурс]. – Режим доступа: http://hyperphysics.phy-astr.gsu.edu/hbase/tables/rstiv.html. 8. M. Bockarjova and G. Andersson, “Transmission Line Conductor Temperature Impact on State Estimation Accuracy”, 2007 IEEE Lausanne Powertech, July 1-5, 2007,Lausanne,Switzerland.