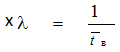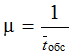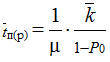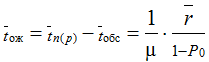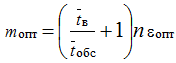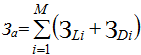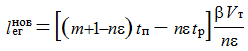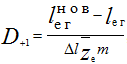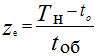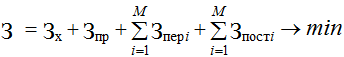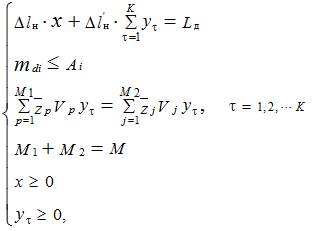ЛОГИСТИЧЕСКАЯ МОДЕЛЬ ОРГАНИЗАЦИИ ПЕРЕВОЗОК НАВАЛОЧНЫХ ГРУЗОВ ДЛЯ ДОРОЖНОГО СТРОИТЕЛЬСТВА
Бережной В.И.1, Бережная Е.В.2
1 профессор, доктор экономических наук, Кубанский государственный университет, филиал в г. Армавир; 2 профессор, доктор экономических наук, Северо-Кавказский федеральный университет
ЛОГИСТИЧЕСКАЯ МОДЕЛЬ ОРГАНИЗАЦИИ ПЕРЕВОЗОК НАВАЛОЧНЫХ ГРУЗОВ ДЛЯ ДОРОЖНОГО СТРОИТЕЛЬСТВА
Аннотация
В статье предложен методический подход к формированию модели организации перевозок навалочных грузов для дорожного строительства с использованием инструментария теории массового обслуживания.
Ключевые слова: логистическая модель, теория массового обслуживания, логистические цепи, автомобильные перевозки, дорожное строительство.
Berezhnoy V.I.1, Berezhnaya E.V.2
1 Professor, Doctor of Economics, Kuban State University, a branch in Armavir; 2 Professor, Doctor of Economics, North-Caucasus Federal University
LOGISTIC MODEL OF ORGANIZATION OF TRANSPORTATION OF BULK CARGO FOR ROAD CONSTRUCTION
Abstract
This paper proposes a methodological approach to the the formation of models for organizing transportation of bulk cargoes for road construction using the tools of queuing theory
Keywords: logistic model, queuing theory, logistics chain, road transport, road construction.
Строительство автомобильных дорог требует координации работы участников технологического процесса, которыми являются предприятия-поставщики щебня, песка, грунта; автоперевозчики, осуществляющие доставку указанных материалов; дорожные строители; автоперевозчики инертных грузов и другие. Поскольку все эти предприятия технологически взаимосвязаны, сбои в работе одного из них отрицательно сказываются на деятельности каждого из участников технологического процессаТехнологический процесс доставки щебня, песка или грунта для строительства автодороги можно представить в виде последовательности следующих этапов:
- груз погружается на железнодорожные платформы (вагоны-самосвалы или полувагоны);
- груз доставляется на ближайшую к месту строительства автомобильной дороги железнодорожную станцию, имеющую накопительную площадку, где происходит самосвальная разгрузка вагонов;
- на накопительной площадке груз с помощью ковшового погрузчика погружается в автомобили-самосвалы;
- груз самосвалами доставляется к месту строительства автодороги.
Поставщики груза, железная дорога, автотранспортные предприятия можно рассматривать как звенья логистической цепи, линейная упорядоченность которых – логистическая цепь – соответствует вышеприведенной последовательности этапов технологии доставки груза.
Данная последовательность этапов доставки имеет особенность, характерную для всех сложных транспортно-технологических систем, состоящую в высокой степени неопределенности, основными источниками которой являются нерегулярность поставок груза и его потребление, неритмичность технологического процесса, статистическая неопределенность продолжительности отдельных операций, ненадежность, проявляющаяся в выходе из строя отдельных технических средств. Для построения логистической цепи важно согласование участников технологического процесса строительства дороги с целью снижения неопределенности.
На наш взгляд, наибольшая степень неопределенности проявляется при взаимодействии автомобильного транспорта с другими звеньями логистической цепи. Поэтому целесообразно рассмотреть согласование работы автомобилей с погрузчиком, работающим на накопительной площадке железнодорожной станции. При формировании логистической цепи важно заранее определить возможные отклонения и проанализировать факторы, их вызывающие.
Рассмотрение возможных отклонений и моделирование множества возможных ситуаций является предметом теории массового обслуживания, которая позволяет расчетным путем проектировать режимы использования транспортных и погрузочно-разгрузочных средств.
Пункт погрузки (накопительная площадка) можно рассматривать как систему массового обслуживания (СМО). Причем интенсивность потока заявок (требований) зависит от состояния системы, что позволяет назвать последнюю замкнутой СМО или СМО Энгсета [1].
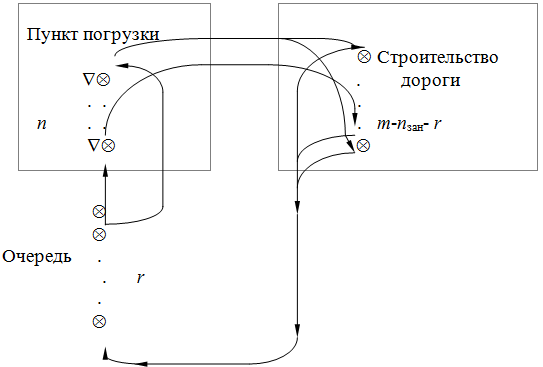
Схема функционирования замкнутой СМО представлена на рисунке 1.
Рис. 1. – Схема функционирования замкнутой системы массового обслуживания на примере погрузки автомобилей
Пусть имеется m автомобилей (источников требований), которые обслуживаются n погрузочными машинами. Каждый автомобиль порождает поток требований на обслуживание, характеризующийся параметром
где ![]() – среднее время возврата автомобиля.
– среднее время возврата автомобиля.
Для рассматриваемого пункта обслуживания
где tоб – среднее время оборота одного автомобиля;
tож – время простоя автомобиля в ожидании обслуживания;
tобс – средняя продолжительность обслуживания.
Параметр потока требований от одного источника требований рассчитывается по формуле (1), пока автомобиль не обслуживается; на время обслуживания поток требований прекращается.
Работа погрузчика характеризуется интенсивностью обслуживания
Заявка, пришедшая от источника (автомобиля) в момент, когда все каналы обслуживания (погрузчики) заняты, становиться в очередь, а автомобили ожидают, пока один из каналов не освободится. Время ожидания в очереди не ограничено.
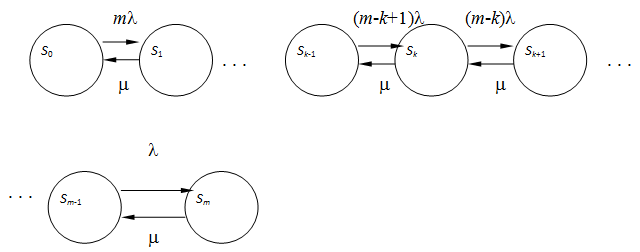
В системе, представленной на рисунке 1, интенсивность поступления автомобилей в пункт погрузки пропорциональна числу автомобилей, находящихся вне пункта, а при отсутствии автомобилей на пункте равна ml. С увеличением количества автомобилей в очереди интенсивность потока уменьшается. Если процесс, протекающий в системе, является марковским, то для вероятностей различных состояний pk(t) (k=1, 2, . . . , m) можно составить систему линейных дифференциальных уравнений, в которой в левой части каждого уравнения проставляется производная ![]() , а в правой части – столько членов, сколько состояний связано непосредственно с данным состоянием. Если стрелка ведет в данное состояние, член имеет знак плюс, если из него, – то минус. Каждый член уравнения равен произведению плотности потока событий, переводящего систему по стрелке связывающей состояния, на вероятность того события, из которого стрелка исходит. Расчеты времени ожидания, погрузки (разгрузки) и других показателей с использованием системы дифференциальных уравнений достаточно трудоемки и громоздки. Однако они значительно упрощается, если в пункте погрузки обслуживает одна погрузочная машина. При строительстве автомобильной дороги на накопительных площадках железнодорожных станций, как правило, погрузку навалочных грузов осуществляет один ковшовый погрузчик или экскаватор, поэтому можно допустить, что упрощенные расчеты отвечают реальным условиям организации погрузки. Граф состояний для системы массового обслуживания, состоящий из одного погрузочного средства, представлен на рисунке 2.
, а в правой части – столько членов, сколько состояний связано непосредственно с данным состоянием. Если стрелка ведет в данное состояние, член имеет знак плюс, если из него, – то минус. Каждый член уравнения равен произведению плотности потока событий, переводящего систему по стрелке связывающей состояния, на вероятность того события, из которого стрелка исходит. Расчеты времени ожидания, погрузки (разгрузки) и других показателей с использованием системы дифференциальных уравнений достаточно трудоемки и громоздки. Однако они значительно упрощается, если в пункте погрузки обслуживает одна погрузочная машина. При строительстве автомобильной дороги на накопительных площадках железнодорожных станций, как правило, погрузку навалочных грузов осуществляет один ковшовый погрузчик или экскаватор, поэтому можно допустить, что упрощенные расчеты отвечают реальным условиям организации погрузки. Граф состояний для системы массового обслуживания, состоящий из одного погрузочного средства, представлен на рисунке 2.
S0 – погрузочный механизм простаивает;
S1 – в систему (на пункт погрузки) поступил и обслуживается один автомобиль;
Sk – в систему поступило k автомобилей или в очереди стоит r-1 автомобилей;
Sm – в системе обслужены все автомобили, очереди нет.
Рис. 2. – Граф состояний системы обслуживания автомобилей в пункте погрузки
Вероятность того, что в систему обслуживания поступило k автомобилей или, что равнозначно, в очереди находится r=k-1 автомобилей,
Среднее число находящихся автомобилей в системе равно
Среднее число обслуживаемых автомобилей равно числу занятых погрузочных средств:
Вероятность того, что погрузочный механизм простаивает,
где χ = μ/λ
Среднее число автомобилей, ожидающих в очереди,
Среднее время простоя автомобиля при погрузке или разгрузке, включая время ожидания
Среднее время пребывания автомобиля в очереди
Плотность распределения времени простоя автомобиля при погрузке или разгрузке
Как видно из приведенных зависимостей, для одной погрузочной машины расчет показателей функционирования СМО относительно прост, и для него достаточно располагать таблицами распределения Пуассона.
Кроме определения времени простоя автомобиля в пункте погрузки важным является расчет оптимального количества транспортных средств. Согласно методике, изложенной в работе [2], оптимальное количество автомобилей можно определить по формуле:
где εопт – коэффициент, соответствующий оптимальному соотношению между простоями транспортных и погрузочно-разгрузочных средств; εопт= 0,8 . . . 0,9.
При оптимальном количестве автомобилей погрузочная техника, занятая погрузкой груза, не будет простаивать. Если количество автомобилей, которыми располагает автотранспортное предприятие, больше оптимального, определенного по формуле (12), то задействовать все автомобили будет не целесообразно, так они значительное время будут простаивать в очереди, и на результатах работы увеличение количества задействованных транспортных средств отразится незначительно.
В расчетах показателей функционирования СМО по приведенным формулам учитывается случайность величины времени простоя автомобиля в пункте погрузки, что объясняется неопределенностью времени ожидания погрузки и времени обслуживания автомобиля, однако в формулах принимается условие постоянности времени оборота автомобиля.
При перевозке дорожно-строительных грузов постоянно увеличивается длина ездки за счет «продвижения» дорожно-строительных работ, и ориентирование на средние значения этого показателя может привести к ошибкам, влияющим на согласование работы транспортной и погрузочно-разгрузочной техники, автотранспортных средств и непосредственно дорожного строительства. Увеличение длины ездки с грузом приводит к увеличению времени оборота автомобиля, что сказывается на количестве транспортной техники, которая может обслуживаться погрузочным средством на согласованных условиях. Это необходимо учесть при согласовании работы автомобилей-самосвалов и погрузочной техники при строительстве дороги. Однако этого будет недостаточно для построения логистической цепи доставки навалочных дорожно-строительных грузов, поскольку при логистическом подходе к управлению транспортировкой принимаются наилучшие решения в соответствии с критерием оптимизации построения логистических систем. Таким критерием при дорожном строительстве может являться, в частности, минимум затрат или минимум времени на доставку навалочных грузов и др.
Рассмотрим построение логистической цепи доставки песка, щебня, грунта и подобных грузов в соответствии с критерием оптимальности - минимум затрат на доставку. При технологической схеме перевозки, включающей железнодорожную и автомобильную составляющие, затраты на доставку можно определить по следующей зависимости:
где Зж – затраты на перевозку железнодорожным транспортом;
Зх – затраты, связанные с хранением груза;
Зпр – затраты на погрузку и разгрузку груза;
За – затраты на перевозку автомобильным транспортом.
Затраты на перевозку автомобильным транспортом в общем виде равны
где М – количество групп (марок) автомобилей с одинаковой грузоподъемностью и затратами;
ЗLi – затраты на использование автотранспортных средств в зависимости от пробега в i-ой группе;
ЗDi – затраты на использование автотранспортных средств в зависимости от количества дней эксплуатации;
Оптимизация затрат на доставку грузов выдвигает задачу выбора автотранспортных средств, использование которых способствует минимизации целевой функции (13). Если в качестве критерия выбора подвижного состава использовать производительность, то, очевидно, выбор будет сделан в пользу автомобилей большей грузоподъемности. Если рассматривать критерий абсолютных затрат на использование техники, то могут быть выбраны автомобили меньшей грузоподъемности. Неоднозначность решения о выборе автотранспортных средств по разным критериям говорит о необходимости учесть при выборе критерия различные аспекты: и производительность, и затраты. Таким критерием могут быть удельные затраты на использование автотранспортных и погрузочных средств за определенный период, например, за один рабочий день, неделю или месяц. Выбирается автомобиль, у которого меньше величина затрат, отнесенная на протяженность участка дороги, обслуженного за период. Малая продолжительность периода оценки работы подвижного состава объясняется переменностью средней длины ездки с грузом.
Минимум удельных затрат на доставку груза как критерий выбора может использоваться для организации оперативного управления транспортным процессом и для предварительных расчетов. Окончательное формирование логистической цепи следует проводить по критерию минимума общих затрат на доставку груза для строительства дороги или ее участка.
При расчете затрат для выбора марки автотранспортного средства делается допущение, что задействуются только автомобили одной группы, остальные – простаивают. Поэтому возникает проблема учета затрат на оплату постоянных издержек для простаивающих автомобилей. Для того чтобы не учитывать эти затраты с целью снижения общих затрат на доставку груза, необходимо четкое календарное планирование перевозок, что позволит учесть в договорах освобождение «неоптимальных» марок автомобилей на определенные дни. Кроме того, незадействованные автомобили могут быть переведены в другой пункт, из которого также ведутся дорожные работы.
При выборе автотранспортных средств необходимо учесть, что интенсивность потока требований, связанных с погрузкой груза, у автомобилей разных марок будет различной. Следовательно, оптимальное количество автотранспортных средств в соответствии с формулой (12) будет разным для разных групп. Поэтому при выборе автотранспортных средств, следует говорить о выборе группы автомобилей с учетом оптимального их количества для согласованной работы транспортной и погрузочной техники.
В отличие от рассмотренного в работе [2] подхода к расчету оптимального количества автомобилей для определения количества самосвалов, обслуживающих дорожное строительство, необходимо учесть переменный характер интенсивности потока требований на обслуживание (погрузку), так как с увеличением длины ездки с грузом возрастает время ездки, что при неизменном количестве автомобилей снижает интенсивность потока заявок.
Снижение интенсивности потока заявок на обслуживание приводит к простою погрузочной техники и к уменьшению количества груза, доставленного к месту проведения дорожно-строительных работ, и, соответственно, к производительности самих работ. Поэтому при некотором снижении интенсивности потока требований количество обслуживаемых в пункте погрузки автомобилей может быть увеличено. Соответствующая автомобиль, определяется по формуле:
длина ездки с грузом, при которой на линию выпускается еще один
Когда известна новая длина ездки с грузом, при которой количество автомобилей на линии может быть увеличено на один, для управления транспортным процессом можно составлять графики выпуска автомобилей на линию по дням работы. Количество дней работы подвижного состава, когда нужно выпускать еще один автомобиль, может быть определено по формуле:
где Δl – средняя длина участка дороги, на строительство которого идет весь объем груза, привезенный одним автомобилем, за время работы m автомобилей;
![]() – среднее число ездок, выполненных за время в наряде одним автомобилем.
– среднее число ездок, выполненных за время в наряде одним автомобилем.
Длина участка дороги, строящегося с использованием груза, доставленного одним автомобилем, может быть определена по следующей зависимости:
где q – грузоподъемность автомобиля, т;
γ– коэффициент использования грузоподъемности, зависящий от класса груза;
Sд – ширина дороги;
hд – высота дороги;
ρг – плотность груза.
Среднее число ездок с грузом, выполненных одним автомобилем за время в наряде, определяется как отношение времени в наряде ко времени ездки. При перевозке строительных грузов коэффициент использования пробега равен 0,5, следовательно
где Тн – время в наряде.
Однако, проводя расчеты по вышеприведенным формулам, мы не учитываем отказы автомобилей, выезжающих на линию, которые могут повлиять на количество единиц подвижного состава на линии. Эксплуатация автомобиля, как известно, может быть представлена как отдельная система массового обслуживания, в которой рассматриваются различные состояния автомобиля: работа на линии, простои в ТО-2, текущем и капитальном ремонтах, простои в выходные и праздничные дни и по другим причинам [3].
Если все автомобили, занятые в обслуживании дорожного строительства, находятся в исправном состоянии и работают на линии, то интенсивность потока заявок на обслуживание в пункте погрузки не изменяется. Как только происходит отказ какого-либо автомобиля или автомобилю необходимо пройти плановое техническое обслуживание или сопутствующий текущий ремонт, интенсивность потока заявок уменьшается. Так как время проведения плановых ремонтно-профилактических работ с автомобилем можно принять за известную величину, можно избежать снижения интенсивности потока заявок на погрузку, а, следовательно, и отклонения от графика доставки необходимого груза. Для этого необходимо иметь возможность заменить выбывший автомобиль аналогичным. В плане выпуска подвижного состава на период проведения работ по ТО и ремонту автомобилей и отмечается замена техники.
Если заменить автомобиль не удается, на время проведения ремонтно-профилактических работ интенсивность потока заявок на обслуживание в пункте погрузки будет снижена. То же характерно для ситуации внеплановых отказов, если нет возможности автомобиль заменить на другой. Если через некоторое время после внезапного отказа на линию выпускается аналогичный автомобиль, график интенсивности восстанавливается.
Итак, основными этапами формирования логистической цепи доставки навалочных грузов для строительства автомобильной дороги в части согласования работы автомобильного транспорта и погрузочной техники являются:
- выбор марки, грузоподъемности и оптимального количества автомобилей для согласованной работы транспортной и погрузочной техники;
- регулирование численности автотранспортых средств с учетом изменяющейся длины ездки для соблюдения согласованной работы автомобилей и пункта погрузки, составление графика выпуска автомобилей на линию;
- учет пробега каждой единицы подвижного состава, обслуживающего строительство дороги, планирование ремонтно-профилактических работ с автомобилями и корректировка графика выпуска автомобилей на линию с учетом этих работ;
- планирование и организация перевозок с учетом минимизации затрат на доставку груза для дорожного строительства.
Для решения последней задачи в качестве вариантов обслуживания строительства дороги может быть рассмотрена следующая схема доставки груза. Груз с накопительной площадки железнодорожной станции перевозится самосвалами большой грузоподъемности на расстояние lег, которое рассчитывается с использованием изложенного подхода. Длина ездки с грузом будет переменной величиной, изменяющейся скачкообразно. Между скачками длина ездки с грузом может приниматься за постоянную величину, что существенно упрощает расчеты. В пунктах разгрузки большегрузных автомобилей создаются промежуточные накопительные площадки, с которых груз автомобилями меньшей грузоподъемности доставляется к месту строительства дороги.
При двухступенчатом варианте доставки функционирует два аналогичных транспортных цикла. Такой вариант перевозок является более сложным, с точки зрения организации транспортного процесса, однако он может обеспечить минимум затрат на доставку груза для дорожного строительства, что очень важно для формирования логистических цепей доставки грузов.
Для определения месторасположения промежуточных накопительных площадок может быть предложена следующая экономико-математическая модель. Целевая функция модели должна иметь вид зависимости (13), однако учитывая, что железнодорожная составляющая затрат на доставку груза неоказывает существенного влияния на расположение промежуточных накопительных площадок, целевая функция с учетом формулы (14) будет иметь вид:
где Зперi – переменные затраты на эксплуатацию автомобилей i-ой марки, руб.;
Зпостi – постоянные затраты на эксплуатацию автомобилей i-ой марки, руб.;
М – количество групп автомобилей разных марок и/или грузоподъемности.
Зх - затраты на хранение груза на накопительной площадке железнодорожной станции,руб
З - Затраты на погрузочные операции,руб
Минимум функции (19) достигается с учетом следующих условий и ограничений:
где Lд – протяженность участка дороги, для строительства которого идет выбор наилучшего варианта доставки грузов, км;
Аi – имеющееся количество автомобилей i-ой группы;
М1 – количество групп автомобилей, доставляющих груз на накопительные площадки;
Δlн – протяженность участка дороги, построенного за время в наряде автомобилями всех групп, работающими совместно, км/дн;
М2 – количество групп автомобилей, перевозящих груз с накопительных площадок;
x – количество дней совместной работы автомобилей всех групп по вывозу груза с накопительной площадки железнодорожной станции, дн.;
K – количество промежуточных накопительных площадок;
yτ – количество дней работы автомобилей, занятых перевозкой грузов на t-ую накопительную площадку большегрузными автомобилями и с нее автомобилями средней грузоподъемности, дн.;
Vp, Vj – объем кузова автомобилей той или иной группы, м3.
Для получения ряда исходных данных модели требуются предварительные расчеты, в частности, имитационное моделирование процесса перевозки дорожно-строительных грузов или обработка статистических данных о перевозочном процессе доставки грузов.
Литература
- Лабскер Л.Г., Бабешко Л.О. Теория массового обслуживания в экономической сфере: Учеб. пособие – М.: Банки и биржи, ЮНИТИ, 1998. – 319 с.
- Воркут А.И. Грузовые автомобильные перевозки (Основы теории транспортного процесса): Учеб. пособие. – Киев: Вища школа, 1979. – 392 с.
- Лукинский В.С., Зайцев Е.И. Прогнозирование надежности автомобилей. – Л.: Политехника, 1991. – 224 с.
References
- Labsker L.G., Babeshko L.O. Teorija massovogo obsluzhivanija v jekonomicheskoj sfere: Ucheb. posobie – M.: Banki i birzhi, JuNITI, 1998. – 319 s.
- Vorkut A.I. Gruzovye avtomobil'nye perevozki (Osnovy teorii transportnogo processa): Ucheb. posobie. – Kiev: Vishha shkola, 1979. – 392 s.
- Lukinskij V.S., Zajcev E.I. Prognozirovanie nadezhnosti avtomobilej. – L.: Politehnika, 1991. – 224 s.