ОБОБЩЁННЫЕ ИСТИННОСТНЫЕ ЗНАЧЕНИЯ: РАЗЛИЧНЫЕ ПОДХОДЫ

 Беликов А. А.¹ Юрина Н. С.²

 ¹Студент, МГУ им. Ломоносова; ²Студентка, МГУ им. Ломоносова

                ОБОБЩЁННЫЕ ИСТИННОСТНЫЕ ЗНАЧЕНИЯ: РАЗЛИЧНЫЕ ПОДХОДЫ

                                                                                     Аннотация

Целью данного исследования является демонстрация нового направления в современной философской логике, основанного на неклассической интерпретации понятия истинностного значения. Основная задача работы - выявление наиболее эффективного подхода  к анализу истинностных значений как сложных сущностей, в частности, подхода обобщённых истинностных значений. Данное исследование является значимым не только в теоретической области, но и в сфере практического применения, связанной с компьютерной обработкой информации и построением коммуникативных стратегий.

Ключевые слова: обобщённые истинностные значения, первоуровневая релевантная логика (FDE), логика Данна – Белнапа, неклассическая трактовка истинности

Belikov A. A.¹ Yurina N. S.²

 ¹Student, Lomonosov Moscow State University;  ²Student, Lomonosov Moscow State University

GENERALIZED TRUTH VALUES: DIFFERENT APPROACHES

Abstract

The purpose of this research is to demonstrate a new trend in the modern philosophical logic, based on the non-classical interpretation of the concept of truth value. The main task of the research is to identify the most effective approach to the analysis of truth values as complex entities, in particular the approach of generalized truth values. This research is significant not only in the theoretical field, but also in practical applications associated with computer processing of information and creating communication strategies.

Keywords: generalized truth values, first degree entailment (FDE), Dunn – Belnap logic, non-classical interpretation of truth

Понятие истинностного значения, являющееся одним из ключевых в современной логике, было введено Готлобом Фреге. Он утверждал, что истинностные значения являются особого рода объектами, выступающими в качестве значений предложений. Фреге трактовал их как атомарные абстрактные логические объекты. Однако сегодня существует несколько подходов к семантическим конструкциям, в рамках которых истинностные значения представлены как производные от более простых компонентов. Рассмотрим подробнее некоторые из них:

1.  Означивание формул в мирах Крипке для пропозициональной интуиционистской логики может рассматриваться как приписывание истинностных значения определённого вида. Пустой мир может быть интерпретирован как совокупность ложных высказываний, а максимальный, т.е. множество всех миров в модели, как истинных. Более того, можно рассмотреть непустые подмножества максимального множества как промежуточные истинностные значения. Таким образом, в пропозициональной интуиционистской логике истинностные значения являются производными от некоторых более простых элементов.

2. В качестве примера структурированных истинностных значений можно привести фактор-семантику[1] для многозначной логики, где истинностные значения определены как упорядоченные n-ки классических истинностных значений. Например, значение 3/8 может быть интерпретировано, как И-Л последовательность длины восемь, содержащая в точности три вхождения И. В данном случае классические значения И (истина) и Л (ложь) используются как вспомогательные блоки для неклассических истинностных значений.

Идея трактовки истинностных значений как сложных сущностей согласуется с подходом, который рассматривает истинностные значения как некоторые подмножества множества классических истинностных значений. Подобный подход можно встретить в работах Данна и Белнапа:

3. Идея создания логики обобщённых истинностных значений принадлежит Данну, которым впервые была построена обобщённая релевантная логика. Он исходил из идеи пресыщенных оценок и истинностно-значных провалов. В первом случае формула может принять оба значения из множества {и, л}, во втором случае она не принимает ни одного из этих значений. Далее Данн задаёт обобщённую функцию приписывания значений: оценка понимается как функция, значениями которой являются не элементы множества {и, л}, а подмножества этого множества. Тогда произвольной формуле можно приписать следующие значения:

1)   { и };      3) { и, л };

2)   { л };      4) .

Таким образом, происходит обобщение множества классических истинностных значений, а так же обобщение функции приписывания значений.

4. Другой вариант обобщения связан с парадигмой рассуждающего компьютера Белнапа. Белнап рассматривает четыре ситуации, в которых оказывается компьютер, разбирающий поступающую к нему информацию:

1)   Компьютеру была сообщена только истина, этому соответствует значение T.

2)   Компьютеру была сообщена только ложь, этому соответствует значение F.

3)   Компьютеру были сообщены и истина, и ложь одновременно, этому соответствует значение B.

4)   Компьютеру не были сообщены ни истина, ни ложь, этому соответствует значение N.

Можно следующим образом проинтерпретировать ситуации, в которых оказывается компьютер Белнапа:

1)   Значение T соответствует { и }.

2)   Значение F соответствует { л }.

3)   Значение B соответствует { и, л }.

4)   Значение N соответствует .

Белнап показал, что четыре обобщённых значения истинности образуют дистрибутивную решётку с дополнением Де Моргана. Логическая решётка соответствует релевантной логике первого уровня, где значение T является максимальным элементом, а F - минимальным. В информационной проекции максимальным элементом является B, минимальным - N. Совмещение этих решёток в одной алгебраической структуре приводит к понятию бирешётки с двумя отношениями порядка: логическим и информационным:

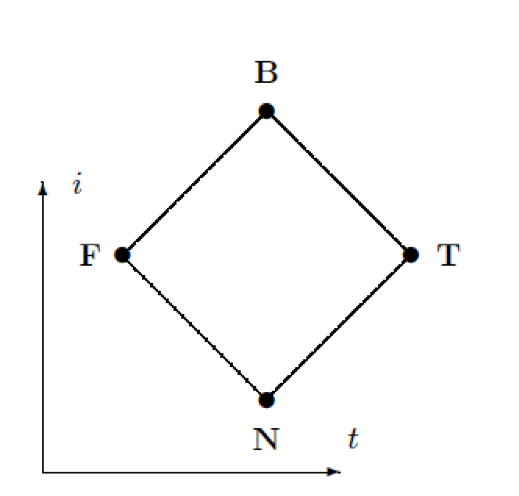
Далее идею обобщённых истинностных значений развили Шрамко и Ванзинг[2], которые связали её с понятием мультирешётки, являющимся обобщением бирешётки. Они обобщили логику Белнапа до шестнадцатизначной логики компьютерной сети. Получившаяся логика совпала с системой выводимостей FDE, т. е. с первоуровневой релевантной логикой.

Ещё одним примером развития идеи обобщённых истинностных значений является логика ETL (ExactlyTrueLogic), построенная Ривеччио. Эта система представляет собой первоуровневую релевантную логику (FDE) с одним выделенным значением T. Такой выбор обусловлен желанием устранить противоречивую информацию из класса истинных высказываний FDE.

5. Новое развитие четырёхзначная логика Белнапа получила в работе Джозефа Кампа, который развивает идею семантики запутанной мысли. Суть её в следующем: существует рациональный субъект, который перепутал очень похожие объекты aи b. Он использует для их обозначения одно имя C. Этот субъект делает заявление, например, о том, что C обладает некоторым свойством. Возникает вопрос: как оценить это заявление, если объект a обладает этим свойством, а b - нет. Камп выступает против приписывания истинностных значений такого рода утверждениям и выдвигает семантику, где характеристиками суждений являются "полезность" и "высокая цена". Утверждение S полезно, если можно извлечь выгоду из того, что S. Утверждение S является дорогостоящим, если наличие S вызовет появление издержек, например, неудачи в достижении поставленной цели. Если наш "сомневающийся субъект" задаёт некоторым внешним наблюдателям вопрос: обладает ли C некоторым свойством, то возможны четыре ответа:

1)   Да ( обозначаем это утверждение с помощью Y );

2)   Нет (обозначаем это утверждение с помощью N );

3)   Не могу сказать ( обозначаем это утверждение с помощью ? );

4)   Да и нет ( обозначаем это утверждение с помощью Y & N ).

Заметим, что наши внешние наблюдатели, которые отвечают на вопрос, не являются "запутанными". При этом они подразумевают разные объекты под значением C. Камп задумал эти четыре возможных ответа, рассматривая эпистемические свойства высказываний как вариант семантических значений, интерпретируя их следующим образом: значение Y является индикатором полезности, значение N - индикатор издержек, значение ? не является индикатором, значение Y & N включает в себя и выгоду, и издержки. Можно провести аналогию между этой семантикой и четырёхзначной логикой Белнапа. И действительно, как заключает Камп, множество выводимостей в его семантике совпадает с множеством выводимостей FDE.

6. Последний рассматриваемый здесь вариант логики обобщённых истинностных значений был недавно предложен  Д. Зайцевым и Я. Шрамко. Этот подход предусматривает разграничение, по крайней мере, двух трактовок истинности: онтологической (истина – значение декларативного предложения, его референциальная характеристика) и эпистемологической (истина – свойство, которое сохраняется при переходе от посылок к заключению в конкретном рассуждении). Таким образом, можно различить два понимания истины: референциальную истину как абстрактный объект, выступающий в качестве значения высказывания, и инференциальную истину как оценку высказывания, которая переносится в правильном рассуждении с посылок на заключение.

Если для формул допускаются как референциальные, так и инференциальные истинностные значения, то можно описать общую семантическую структуру, необходимую для их интерпретации. В качестве базиса такой структуры используется множество {t}  {1}, где t представляет

собой референциальную истину, а 1 – инференциальную. Применяя

процедуру обобщения, получаем следующие значения:

1)   < T, 1> - T1 (предложение объективно истинно и принимается);

2)   < T, 0> - T0 (предложение объективно истинно, но отвергается);

3)   <F, 1>  - F1 (предложение объективно ложно, но принимается);

4)   <F, 0 > - F0 (предложение объективно ложно и отвергается).

Если задать на множестве этих истинностных значений стандартные теоретико-множественные операции пересечения и объединения, то получается четырёхэлементная решётка:

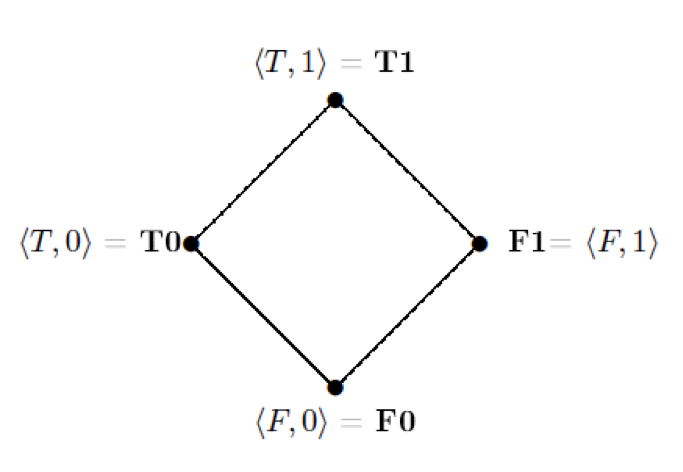
Подводя итоги, стоит отметить, что работа в области обобщённых истинностных значений открывает широкие перспективы не только в области теоретико-логических исследований (построения семантик, исчислений, использования различных методов доказательств метатеоретических свойств), но и в сфере практической деятельности: анализа информации компьютерными устройствами, а также создания аргументативных стратегий.

Литература

1. Г. Фреге «О смысле и значении».

2. Karpenko A. Factor semantics for n-valued logics // Studia Logica. – 1983. - № 42. – P. 179-185.

3. Belnap N. D.  How a computer should think // Contemporary Aspects of Philosophy // Oriel Press. – 1977. - P. 30-50.

4. Pietz A., Rivieccio U. Nothing but the truth // Journal of philosophical logic. – 2013. - Vol. 42, issue 1. – P. 125 – 135.

5. Camp J.  Confusion: A study in the Theory of Knowledge // Cambrige, MA: Harvard University Press, 2002.

6. Zaitsev D., Shramko Y. Bi-facial Truth: a Case for Generalized Truth Values // Studia Logica // Kluwer Academic Publishers (Netherlands). -  2013. -  Vol. 101, № 6. – P. 1299-1318.

[1] Подробнее о фактор – семантике см. Karpenko A. “Factor semantics for n-valued logics”

[2] Подробнее о шестнадцатизначной логике см. Shramko Y. and H. Wansing “Some useful sixteen-valued logics: How a computer network should think”.