О ТЕНЗОРНОМ РАСШИРЕНИИ ОДНОЙ КЛАССИЧЕСКОЙ ГАМИЛЬТОНОВОЙ СИСТЕМЫ
Берзин Д.В.
Кандидат физико-математических наук, доцент Финансового университета при Правительстве Российской Федерации, Москва
О ТЕНЗОРНОМ РАСШИРЕНИИ ОДНОЙ КЛАССИЧЕСКОЙ ГАМИЛЬТОНОВОЙ СИСТЕМЫ
Аннотация
Операция тензорного расширения занимает важное место в теории гамильтоновых систем. В статье рассмотрены соответствующие перестройки (бифуркации) на примере тензорного расширения классической задачи Эйлера о движении твердого тела.
Ключевые слова: Гамильтоновы системы, задача Эйлера, тензорные расширения, бифуркации.
Berzin D.V.
PhD in Physics and Mathematics, associate professor, Financial University under the government of Russian Federation
ABOUT TENSOR EXTENTION OF A CLASSIC HAMILTONIAN SYSTEM
Abstract
Tensor extension takes an important part in Hamiltonian systems. We consider bifurcations in tensor extension of classical Euler problem.
Keywords: Hamiltonian systems, Euler problem, tensor extensions, bifurcations.
Как было отмечено в [1] и [2], в теории интегрируемых гамильтоновых систем важным является метод тензорного расширения алгебр Ли, который впервые был предложен В.В.Трофимовым [3], а затем развит А.В.Браиловым [4]. Этот метод, в частности, дает весьма эффективный способ построения инволютивных семейств функций на орбитах коприсоединенного представления групп Ли. Особое место здесь занимает тензорное расширение алгебр Ли посредством фактор-кольца ![]() . Имеется алгоритм, принадлежащий С.Ж.Такиффу [5] и В.В.Трофимову [3], позволяющий из интегралов и инвариантов для исходной алгебры Ли получить соответствующие интегралы и инварианты для расширенной алгебры. В частности, с помощью этого алгоритма можно из классических и известных систем получать интегрируемые системы с перестройками некомпактных инвариантных подмногообразий.
. Имеется алгоритм, принадлежащий С.Ж.Такиффу [5] и В.В.Трофимову [3], позволяющий из интегралов и инвариантов для исходной алгебры Ли получить соответствующие интегралы и инварианты для расширенной алгебры. В частности, с помощью этого алгоритма можно из классических и известных систем получать интегрируемые системы с перестройками некомпактных инвариантных подмногообразий.
Известно, что движение трехмерного твердого тела вокруг точки, закрепленной в центре масс, можно описать уравнениями Эйлера для алгебры Ли ![]() группы движений трехмерного евклидового пространства. Такие системы гамильтоновы на четырехмерных орбитах коприсоединенного представления (диффеоморфных касательному расслоению двумерной сферы) и для полной интегрируемости по Лиувиллю кроме гамильтониана H указывается еще один (дополнительный) интеграл K.
группы движений трехмерного евклидового пространства. Такие системы гамильтоновы на четырехмерных орбитах коприсоединенного представления (диффеоморфных касательному расслоению двумерной сферы) и для полной интегрируемости по Лиувиллю кроме гамильтониана H указывается еще один (дополнительный) интеграл K.
В результате тензорного расширения получаем 12-мерную алгебру Ли ![]() . Имеем отображение момента
. Имеем отображение момента ![]() – орбита общего положения коприсоединенного представления для тензорного расширения,
– орбита общего положения коприсоединенного представления для тензорного расширения, ![]() , где
, где ![]() – инволютивный относительно скобки Пуассона-Ли набор, получаемый из
– инволютивный относительно скобки Пуассона-Ли набор, получаемый из ![]() при тензорном расширении [5]. Доказывается, что орбита
при тензорном расширении [5]. Доказывается, что орбита ![]() общего положения диффеоморфна
общего положения диффеоморфна ![]() – двумерная сфера.
– двумерная сфера.
Рассмотрим перестройки типа "центр" (обозначим через "A") и "седло" (обозначим через "B"). В канонических координатах в окрестности начала координат двумерной плоскости они задаются отображениями [7]:
(1) ![]() (центр)
(центр)
(2) ![]() (седло)
(седло)
Теорема 1. В результате операции тензорного расширения особенности "центр" и "седло", заданные в локальных канонических координатах ![]() выражениями (1) и (2), перейдут во особенности, определяемые (3) и (4) соответственно:
выражениями (1) и (2), перейдут во особенности, определяемые (3) и (4) соответственно:
(3) ![]() ,
,
(4) ![]() .
.
При этом отображения момента ![]() заданы в окрестности точки
заданы в окрестности точки ![]() в четырехмерном симплектическом пространстве
в четырехмерном симплектическом пространстве ![]() . Особенности нулевого ранга (3) и (4) – вырожденные и относятся к типам 14a и 14b соответственно (см. таблицу в конце [8]).
. Особенности нулевого ранга (3) и (4) – вырожденные и относятся к типам 14a и 14b соответственно (см. таблицу в конце [8]).
Анализируя отображения момента (3) и (4), мы приходим к следующей теореме.
Теорема 2. Из перестроек A и B при тензорном расширении возникают перестройки T(A), R(A), T(B), R(B) соответственно, которые можно представить так:
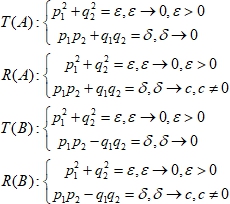
Литература
- Берзин Д.В. Особенности "центр" и "седло" в тензорных расширениях некоторых гамильтоновых систем – Международный научно-исследовательский журнал, №2 (9), 2013, с. 4
- Берзин Д.В. Перестройки "центр" и "седло" в тензорном расширении задачи Эйлера – Международный научно-исследовательский журнал, №3 (10), 2013, с. 19
- Трофимов В.В. Расширения алгебр Ли и гамильтоновы системы – Изв. АН СССР, серия матем., 1983, т.47, № 6, с. 1303-1321
- Браилов А.В. Инволютивные наборы на алгебрах Ли и расширения кольца скаляров / Вестник МГУ, Сер.1 Математика, механика / 1983, №1, с. 47-51
- Takiff S.J. Rings of invariant polynomials for a class of Lie algebras. –Trans. Amer. Math. Soc., 1971, V.160, p.249-262
- Берзин Д.В. Инварианты коприсоединенного представления для алгебр Ли некоторого специального вида – Успехи мат. наук, 1996, т.51, №1, с.141
- Eliasson L. Normal forms for Hamiltonian systems with Poisson commuting integrals. Elliptic case – Comment.Math.Helvetici, №65, 1990, p.4-35
- Lerman L.M., Umanskii Ya.L. Structure of the Poisson action of on a four-dimensional symplectic manifold – Selecta Mathematica Sovietica, 1987, v.6, №4, p.365-396.
