ЛИНЕЙНАЯ И КВАДРАТИЧНАЯ РЕГРЕССИОННЫЕ МОДЕЛИ ПОКРОВНЫХ МАТЕРИАЛОВ ТЕПЛОЗАЩИТНОЙ ОДЕЖДЫ ДЛЯ НЕФТЯНИКОВ
Иващенко И.Н.1, Шмалько С.П. 2
1Кандидат технических наук, доцент, Кубанский государственный университет, 2кандидат педагогических наук, доцент Академия маркентинга и социально-информационных технологий
ЛИНЕЙНАЯ И КВАДРАТИЧНАЯ РЕГРЕССИОННЫЕ МОДЕЛИ ПОКРОВНЫХ МАТЕРИАЛОВ ТЕПЛОЗАЩИТНОЙ ОДЕЖДЫ ДЛЯ НЕФТЯНИКОВ
Аннотация
В статье представлены исследования взаимосвязей между выборками показателей теплофизических параметров покровных материалов теплозащитной одежды для их оптимального использования.
Ключевые слова: теплоизоляция, свойства материалов, одежда.
Ivaschenko I.N. 1, Shmalko S.P. 2
1Ph.D., Associate Professor, Kuban State University, 2Ph.D., associate professor of the Academy and the marketing of social and information technology
LINEAR AND QUADRATIC REGRESSION MODEL OF COATING MATERIALS HEAT-SHIELDING CLOTHES FOR PETROLEUM
Аbstract
The paper presents the study of interrelations between sampling thermal parameters of coating materials heatproof clothing for optimal use.
Keywords: thermal insulation properties of materials , clothing.
Появление текстильных материалов с новыми свойствами и развитие компьютерных технологий существенно изменили традиционные подходы к процессам проектирования и производства теплозащитной одежды. Так рациональное сочетание свойств покровной ткани (слоя) и теплоизоляционного слоя позволяет значительно улучшить теплозащитные функции одежды, однако такие рекомендации для швейной отрасли отсутствуют.
На теплоизоляцию одежды оказывают влияние теплофизические (тепловое сопротивление, теплопроводность, теплоемкость) и структурные (пористость, средняя плотность, толщина) показатели свойств материалов, применяемых в комплекте теплозащитной одежды. Ранее одним из авторов [1] были проведены исследования по установлению влияния вредных производственных и климатических факторов на организм человека, произведен ориентировочный расчет необходимой теплоизоляции защитной одежды, время допустимого непрерывного пребывания на холоде на примере нефтедобывающего производства южного климатического региона России.
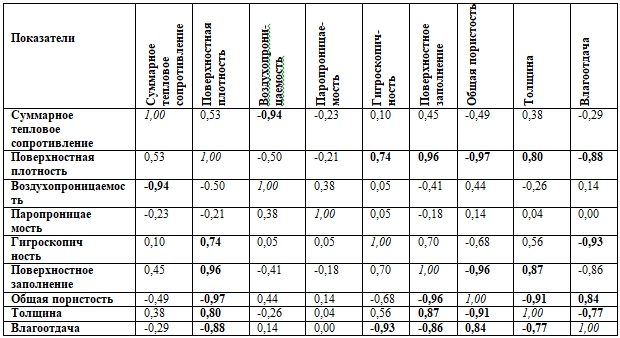
Задачей нашего исследования было изучение взаимосвязей между предоставленными выборками показателей теплофизических параметров покровных материалов многофункциональной структуры теплозащитной одежды. Обработка данных была произведена методом корреляционного анализа с помощью программного обеспечения StatSoft STATISTICA 8.0. Результаты показали существенные взаимосвязи (значимые показатели выделены жирным шрифтом при p˂0,5000) некоторых структурных характеристик покровных материалов, они представлены в виде матрицы коэффициентов корреляции (табл. 1).
Таблица 1 – Матрица коэффициентов корреляции структурных характеристик покровных материалов
Полученная матрица позволила установить характер линейных взаимосвязей самых различных показателей между собой. Так признак суммарного теплового сопротивления имеет обратную устойчивую взаимосвязь с факторами: воздухопроницаемости, поверхностной плотности. В связи, с чем они были выбраны в качестве зависимых показателей, а независимым показателем – паропроницаемость, она либо не влияет на суммарное тепловое сопротивление, либо влияет, но нелинейно.
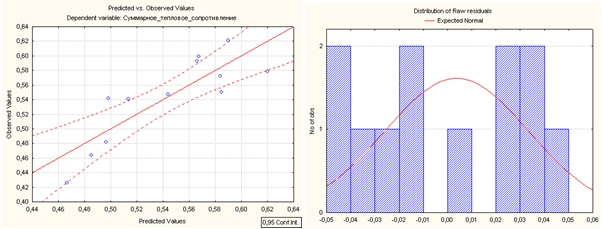
Рассчитав линейную множественную регрессию (Рис.1) взаимосвязи суммарного теплового сопротивления (U) с поверхностной плотностью (X), с воздухопроницаемостью (Y) и с паропроницаемостью (Z), нами было получено уравнение (1) с коэффициентом корреляции R=0,8461 и уровнями значимости для коэффициентов линейной регрессии: поверхностной плотности – 0,03; воздухопроницаемости – 0,02 и паропроницаемости – 0,29.
U=0,4015+0,0006X-0,0027Y+0,0058Z (1)
Рис. 1 – Линейная множественная регрессия взаимосвязи суммарного теплового сопротивления с поверхностной плотностью, и воздухопроницаемостью, а также с паропроницаемостью
Качество линейной множественной регрессии можно признать удовлетворительным, так как относительная погрешность составляет менее 10%, несмотря на то, что остатки распределёны не по нормальному закону для случайных величин.
На следующем этапе была уточнена линейная множественная регрессия суммарного теплового сопротивления, зависящая только от двух факторов: поверхностной плотности и воздухопроницаемости (таблица 2) в связи с тем, что уровень значимости коэффициента паропроницаемости линейной регрессии высок (0,29), а предоставленная выборка имеет не слишком большой объём.
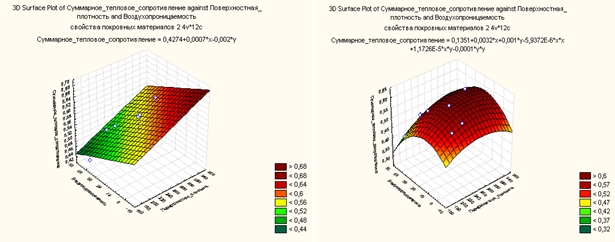
В результате чего было получено уравнение линейной множественной регрессии (2) взаимосвязи суммарного теплового сопротивления (U) с поверхностной плотностью (X) и воздухопроницаемостью (Y), графическая иллюстрация которого представлена на рисунке 2. Коэффициент корреляции в данном случае R=0,8185 и уровни значимости коэффициентов линейной регрессии: для поверхностной плотности – 0,02; для воздухопроницаемости –0,02.
U = 0,4274 + 0,0007∙X – 0,0020∙Y (2)
Так как индекс корреляции линейной множественной регрессии взаимосвязи суммарного теплового сопротивления с двумя факторами на 0,0276 меньше, чем индекс корреляции линейной множественной регрессии с тремя факторами и погрешность менее 10%, то отсутствие фактора паропроницаемости незначительно повлияло на результат.
Сравним полученное линейное уравнение (2) с уравнением квадратической множественной регрессии (3) суммарного теплового сопротивления (U) для двух значимых переменных: поверхностной плотности (X) и воздухопроницаемости (Y), графическая иллюстрация которого представлена на рисунке 2.
U=0,1351+0,0032∙X+0,001∙Y–5,9372Е-6∙X2+1,1726Е-5XY-0,0001Y2 (3)
Рис. 2 – Линейная и квадратическая множественные регрессии взаимосвязи суммарного теплового сопротивления с поверхностной плотностью и воздухопроницаемостью
Качество и точность модели изменяются незначительно, её улучшение достигается за счёт увеличения количества параметров. Но если выбирать из трёх полученных моделей лучшую, то на наш взгляд более удачной является квадратическая множественная модель с двумя факторами.
Литература
- Иващенко И.Н., Беляева С.А. Проектирование теплозащитной специальной одежды для работников нефтедобывающей отрасли. /Монография/ Краснодар, 2012. – 110 с.