ЧИСЛЕННОЕ ИССЛЕДОВАНИЕ КОЛЕБАТЕЛЬНЫХ ПРОЦЕССОВ В ХИМИЧЕСКОЙ КИНЕТИКЕ НА ОСНОВЕ МЕТОДА РОЗЕНБРОКА С КОМПЛЕКСНЫМИ КОЭФФИЦИЕНТАМИ
Икрамов Р.Д.1 Мустафина С.А.2
1Аспирант, Стерлитамакский филиал Башкирского Государственного Университета;
2Доктор физико-математических наук, Стерлитамакский филиал Башкирского Государственного Университета;
ЧИСЛЕННОЕ ИССЛЕДОВАНИЕ КОЛЕБАТЕЛЬНЫХ ПРОЦЕССОВ В ХИМИЧЕСКОЙ КИНЕТИКЕ НА ОСНОВЕ МЕТОДА РОЗЕНБРОКА С КОМПЛЕКСНЫМИ КОЭФФИЦИЕНТАМИ
Аннотация
В работе рассмотрена модель модифицированного Орегонатора, описывающий поведение реакции Белоусова-Жаботинского, с учетом протекания реакции в реакторе постоянного объема с обменом вещества, описан и применен к модели метод Розенброка с комплексными коэффициентами для решения жесткой системы дифференциальных уравнений.
Ключевые слова: Орегонатор, метод Розенброка, колебания.
Ikramov R.D.1, Mustafina S.A.2
1Postgraduate student, Sterlitamak branch of the Bashkir State University
PhD in Physics and mathematics, Sterlitamak branch of the Bashkir State University
NUMERICAL RESEARCH OF OSCILLATORY PROCESSES IN CHEMICAL KINETICS BY ROSENBROCK METHOD WITH COMPLEX COEFFICIENTS
Abstract
In this article we consider a modified model Oregonator describing the behavior of Belousov-Zhabotinsky reaction, given the reaction in the reactor with constant volume metabolism. Described and applied to the model Rosenbrock method with complex coefficients for solving stiff systems of differential equations.
Keywords: Oregonator, Rosenbrok method, oscillations.
Химические превращения протекают, как правило, по многостадийным схемам. Изменения концентраций исходных веществ и промежуточных продуктов во времени далеко не всегда описываются возрастающими или убывающими кривыми – могут наблюдаться участки постоянства или очень малого изменения концентрации того или иного компонента, кривые с перегибом. Детальное исследование кинетики сложных процессов показало, что при наличии обратной связи вдали от равновесия возможно возникновение колебательных режимов – периодическое возрастание или уменьшение концентрации одного из компонентов во времени. При численном исследовании колебательных реакций возникает проблема решения жесткой системы обыкновенных дифференциальных уравнений, для решения которой необходимо использовать специальные методы, основанные на неявных расчетных схемах[1]. Целью настоящего исследования является разработка алгоритма и программы для решения прямой кинетической задачи и исследования многокомпонентных химических систем со сложной нелинейной динамикой.
Рассмотрим химический процесс в рамках сосредоточенной модели изотермического реактора постоянного объема, которому соответствует система обыкновенных дифференциальных уравнений ![]() с заданным начальным условием
с заданным начальным условием ![]() , где
, где ![]() – стехиометрическая матрица,
– стехиометрическая матрица, ![]() – соответственно вектор концентраций реагентов и скоростей стадий. Если реакция протекает в изотермическом реакторе постоянного объема с обменом вещества (открытая система, реактор идеального смешения), то система дифференциальных уравнений записывается в виде
– соответственно вектор концентраций реагентов и скоростей стадий. Если реакция протекает в изотермическом реакторе постоянного объема с обменом вещества (открытая система, реактор идеального смешения), то система дифференциальных уравнений записывается в виде ![]() – вектор концентраций реагентов на входе,
– вектор концентраций реагентов на входе, ![]() – время пребывания смеси в реакторе, υ – объем реактора, λ – объемная скорость течения смеси через реактор. В качестве тестового примера используем модель модифицированного Орегонатора, дающего сложный предельный цикл и состоящий из 6 стадий[2]:
– время пребывания смеси в реакторе, υ – объем реактора, λ – объемная скорость течения смеси через реактор. В качестве тестового примера используем модель модифицированного Орегонатора, дающего сложный предельный цикл и состоящий из 6 стадий[2]:
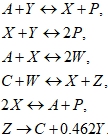
В данной реакции участвуют 7 частиц, имеющие обозначения: ![]()
![]() . В этих обозначениях
. В этих обозначениях ![]() – ион металла катализатора, а
– ион металла катализатора, а ![]() – окисленная форма этого иона. Обозначим концентрации реагентов следующим образом:
– окисленная форма этого иона. Обозначим концентрации реагентов следующим образом:![]()
![]() . Соответствующая система дифференциальных уравнений состоит из 7 уравнений вида[2]:
. Соответствующая система дифференциальных уравнений состоит из 7 уравнений вида[2]:
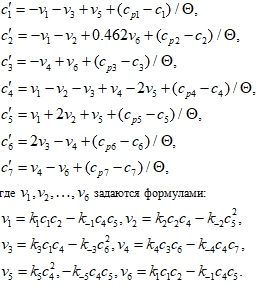
Коэффициенты скоростей реакции принимают следующие значения (моль/с): ![]()
![]()
Для численного исследования модели модифицированного Орегонатора был выбран двухстадийный метод Розенброка с комплексными коэффициентами. Схемы метода Розенброка для перехода на новый временной слой требуют решения линейной системы уравнений с хорошо обусловленной матрицей, что позволяет избежать итераций. В простейшем случае методы типа Розенброка могут иметь вид[3]:
![]() ,
,
где ![]() находятся из соответствующих систем линейных уравнений:
находятся из соответствующих систем линейных уравнений:
![]()
Здесь ![]() – численное решение задачи (1), h – шаг по времени, E – единичная матрица,
– численное решение задачи (1), h – шаг по времени, E – единичная матрица, ![]() – матрица Якоби системы (1), а
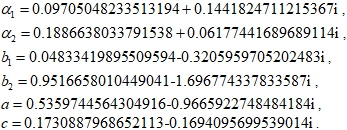
– матрица Якоби системы (1), а ![]() – комплексные параметры, определяющие свойства схемы. В [3] приводятся следующие значения:
– комплексные параметры, определяющие свойства схемы. В [3] приводятся следующие значения:
Интегрирование велось с шагом 0.0001 на интервале ![]() . Результаты интегрирования, представленные на рис.1–рис.2, показывают удовлетворительное согласование с результатами работы [2], полученными (2,1)-методом решения жестких систем, который значительно усложнен нахождением матрицы производных второго порядка и большим числом элементарных операций над матрицами. Такие операции оказывают влияние на скорость алгоритма при высоких размерностях. Созданный авторами алгоритм и программа на основе схемы Розенброка для решения прямой задачи химической кинетики могут быть адаптированы к другим колебательным реакциям путем замены правых частей системы обыкновенных дифференциальных уравнений и начальных условий.
. Результаты интегрирования, представленные на рис.1–рис.2, показывают удовлетворительное согласование с результатами работы [2], полученными (2,1)-методом решения жестких систем, который значительно усложнен нахождением матрицы производных второго порядка и большим числом элементарных операций над матрицами. Такие операции оказывают влияние на скорость алгоритма при высоких размерностях. Созданный авторами алгоритм и программа на основе схемы Розенброка для решения прямой задачи химической кинетики могут быть адаптированы к другим колебательным реакциям путем замены правых частей системы обыкновенных дифференциальных уравнений и начальных условий.
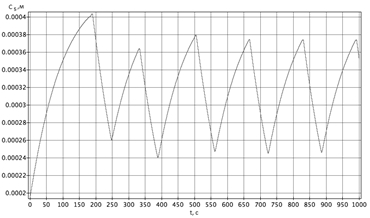
Рис. 1 - Колебания значений концентрации реагента c5 в зависимости по времени
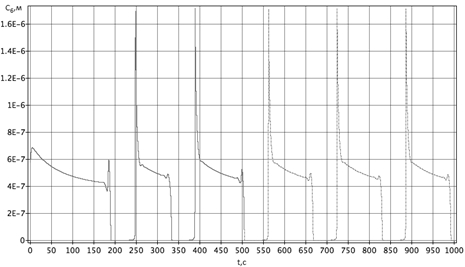
Рис. 2 - Колебания значений концентрации реагента c6 по времени
Литература
- Икрамов Р.Д. Моделирование автоколебательных режимов // Молодежные инновации в машиностроении: cб. тезисов межвузовской студенческой научно-практической конференции (Ишимбай, 10-12 апр. 2014г.). Ишимбай: УГАТУ, 2014. – С. 53.
- Новиков E.А. Численное моделирование модифицированного орегонатора (2,1)-методом решения жестких задач // Вычислительные методы и программирование. – 2010. – Т. 11. – C. 281-288.
- Лимонов А.Г. Разработка двухстадийных схем Розенброка с комплексными коэффициентами и их применение в задачах моделирования образования периодических наноструктур: Автореф. дис. канд. физ.-мат. наук. – Екатеринбург, 2010. – 23 с.
