МЕТОДЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ И ТЕОРИЯ ВЕРОЯТНОСТЕЙ В БИРЖЕВОЙ ТОРГОВЛЕ
МЕТОДЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ И ТЕОРИЯ ВЕРОЯТНОСТЕЙ В БИРЖЕВОЙ ТОРГОВЛЕ
Аннотация
Биржевая торговля является сложной и динамичной сферой. Методы математической статистики и теории вероятностей являются неотъемлемой частью биржевой торговли, где точность анализа и прогнозирования имеет решающее значение. Они позволяют трейдерам и инвесторам основывать свои решения на объективных данных и статистических закономерностях, а не на случайностях или эмоциональных реакциях. Модели временных рядов, такие как ARIMA и GARCH, позволяют учесть тренды, сезонности и волатильность, предоставляя более точные прогнозы и оценки рисков. Такие методы помогают выявить цикличность и повторяемость в ценовых движениях, что способствует принятию обоснованных решений по входу и выходу с рынка. Кроме того, математическая статистика и теория вероятностей предоставляют инструменты для оценки вероятностей успеха или неудачи торговых стратегий и определения оптимального уровня риска. В целом, эти методы способствуют повышению эффективности торговли и минимизации потерь, позволяя трейдерам и инвесторам принимать информированные решения на основе статистических данных.
1. Введение
Представленная работа посвящена рассмотрению методов математической статистики и теории вероятностей в контексте биржевой торговли.
Анализ временных рядов представляет собой процесс изучения последовательности данных, упорядоченных во времени, с целью выявления закономерностей, трендов, сезонности и других характеристик. В контексте биржевой торговли временные ряды представляют цены активов, такие как акции, валюты или сырьевые товары, в течение определенного периода времени.
2. Основная часть
Цель данной статьи состоит в исследовании и анализе применения методов математической статистики и теории вероятностей в контексте биржевой торговли с целью выявления тенденций, сезонности и оценки волатильности рынка.
Задачи:
1. Обзор методов анализа временных рядов в биржевой торговле, включая визуализацию данных, статистический анализ, модели временных рядов (ARIMA, GARCH) и портфельный анализ.
2. Исследование роли математической статистики и теории вероятностей в предсказании изменений цен активов на рынке.
3. Оценка рисков и доходности портфеля с использованием основных понятий математической статистики и теории вероятностей.
4. Применение симуляции Монте-Карло для моделирования различных сценариев доходности и рисков портфеля.
Для анализа временных рядов в биржевой торговле используются различные методы, которые позволяют исследовать структуру, тренды, цикличность и случайные колебания в данных. Рассмотрим некоторые из этих методов.
Первым шагом в анализе временных рядов является визуализация данных. Графическое представление временного ряда позволяет исследовать его основные характеристики, такие как тренды, сезонность и выбросы. Графики, такие как линейные графики, графики скользящего среднего и графики автокорреляции, помогают выявить закономерности и структуру в данных .
Статистический анализ временных рядов включает оценку статистических характеристик, таких как среднее значение, дисперсия, автокорреляция и прочие моменты. Автокорреляция позволяет исследовать наличие связи между значениями временного ряда в разные периоды времени. Это может помочь выявить сезонность или иные зависимости в данных .
Для прогнозирования изменений цен активов на бирже широко применяются модели временных рядов, такие как ARIMA и GARCH. Модель ARIMA учитывает тренд, сезонность и случайные колебания в данных, что позволяет предсказывать будущие значения временного ряда. Анализ волатильности, связанный с изменчивостью ценовых движений, может быть исследован с помощью моделей GARCH. Эти модели позволяют оценить и прогнозировать риски, связанные с изменчивостью цен на рынке.
Анализ временных рядов играет важную роль в биржевой торговле, позволяя исследовать структуру и закономерности в ценовых движениях активов. Методы математической статистики, такие как модели авторегрессии (AR) и модели скользящего среднего (MA), используют предыдущие значения временного ряда для прогнозирования будущих значений. Модели ARMA объединяют в себе авторегрессионные и модели скользящего среднего, учитывая и предыдущие значения временного ряда, и случайные ошибки .
Модели ARIMA являются расширением моделей ARMA и включают процесс интегрирования для стационаризации временного ряда. Они учитывают не только предыдущие значения временного ряда и случайные ошибки, но и проводят интегрирование для устранения нестационарности.
Модели GARCH, в свою очередь, специально разработаны для моделирования и прогнозирования волатильности финансовых временных рядов. Они учитывают изменчивость (гетероскедастичность) во временных рядах, что позволяет более точно оценивать и прогнозировать риск .
Все эти математические модели являются важными инструментами для прогнозирования в биржевой торговле и позволяют анализировать и предсказывать ценовые движения и риски на основе исторических данных. Одним из ключевых инструментов для оценки рисков и доходности в биржевой торговле является портфельный анализ. Портфельный анализ позволяет инвесторам оценить, как различные активы в их портфеле взаимодействуют между собой и как они влияют на общую доходность и риск портфеля .
Для оценки рисков и доходности портфеля применяются основные понятия теории вероятностей и математической статистики, а именно:
−математическое ожидание и дисперсия используются для оценки среднего дохода и вариации активов в портфеле. Математическое ожидание показывает ожидаемую доходность актива, а дисперсия измеряет степень колебаний доходности актива. Чем выше дисперсия, тем больше риск связан с активом .
−коэффициент корреляции используется для измерения степени взаимосвязи между доходностями различных активов в портфеле. Корреляция может быть положительной (когда доходности двух активов движутся в одном направлении) или отрицательной (когда доходности двух активов движутся в противоположных направлениях). Низкая или нулевая корреляция между активами может помочь снизить риски в портфеле , .
Существует несколько показателей, которые помогают оценить риски и доходность портфеля, включая коэффициент Шарпа, коэффициент трейна и индекс бета. Коэффициент Шарпа измеряет отношение между доходностью портфеля и его общим риском. Коэффициент трейна показывает соотношение между ожидаемой доходностью и общим риском портфеля. Индекс бета измеряет чувствительность портфеля к изменениям в общем рынке .
Симуляция Монте-Карло является методом моделирования различных сценариев доходности и рисков портфеля. С помощью этого метода можно оценить вероятность различных исходов и сделать более информированные решения в отношении портфеля. Важно отметить, что оценка рисков и доходности является сложным процессом, и требуется учет множества факторов и переменных. Комбинирование различных методов и тщательный анализ позволяют инвесторам принимать обоснованные решения, основанные на ожиданиях доходности и уровне риска.
Приведём анализ временных рядов в биржевой торговле на примере акций Газпрома за 2020-2022г. , .
Для анализа временных рядов акций Газпрома за период с 03.01.2020 по 03.12.2021 года, можно использовать различные методы математической статистики и анализа временных рядов. Рассмотрим некоторые из них.
3. Визуализация временных рядов
Таблица 1 - Цены акций Газпрома с 03.01.2020 по 03.12.2021
Дата | Курс, руб. |
03.01.2020 | 259,00 |
03.02.2020 | 227,64 |
03.03.2020 | 201,48 |
03.04.2020 | 189,77 |
04.05.2020 | 185,70 |
03.06.2020 | 208,00 |
02.07.2020 | 195,65 |
03.08.2020 | 183,25 |
03.09.2020 | 180,01 |
02.10.2020 | 169,47 |
03.11.2020 | 161,09 |
03.12.2020 | 186,04 |
04.01.2021 | 215,73 |
03.02.2021 | 217,12 |
03.03.2021 | 222,95 |
02.04.2021 | 228,40 |
04.05.2021 | 233,05 |
03.06.2021 | 271,60 |
02.07.2021 | 294,35 |
03.08.2021 | 286,97 |
03.09.2021 | 317,94 |
04.10.2021 | 371,00 |
03.11.2021 | 350,74 |
03.12.2021 | 345,99 |
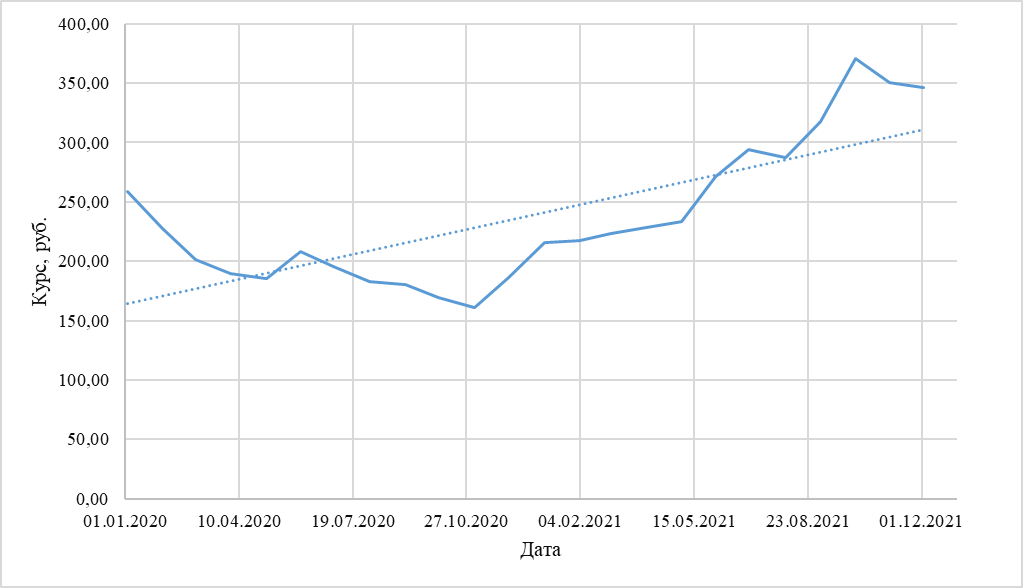
Рисунок 1 - Зависимость курса акций от даты
4. Расчет доходности
Для анализа доходности акций Газпрома, можно рассчитать ежемесячную доходность на основе изменения цен акций. Доходность можно рассчитать по формуле:
Таблица 2 - Доходность на основе изменения цен акций
Период | Доходность |
03.01.2020 – 03.04.2020 | - 26,73 |
03.04.2020 – 02.07.2020 | 3,10 |
02.07.2020 – 02.10.2020 | - 13,38 |
02.10.2020 – 04.01.2021 | 27,30 |
04.01.2021 – 02.04.2021 | 5,87 |
02.04.2021 – 02.07.2021 | 28,87 |
02.07.2021 – 04.10.2021 | 26,04 |
04.10.2021 – 03.12.2021 | - 6,74 |
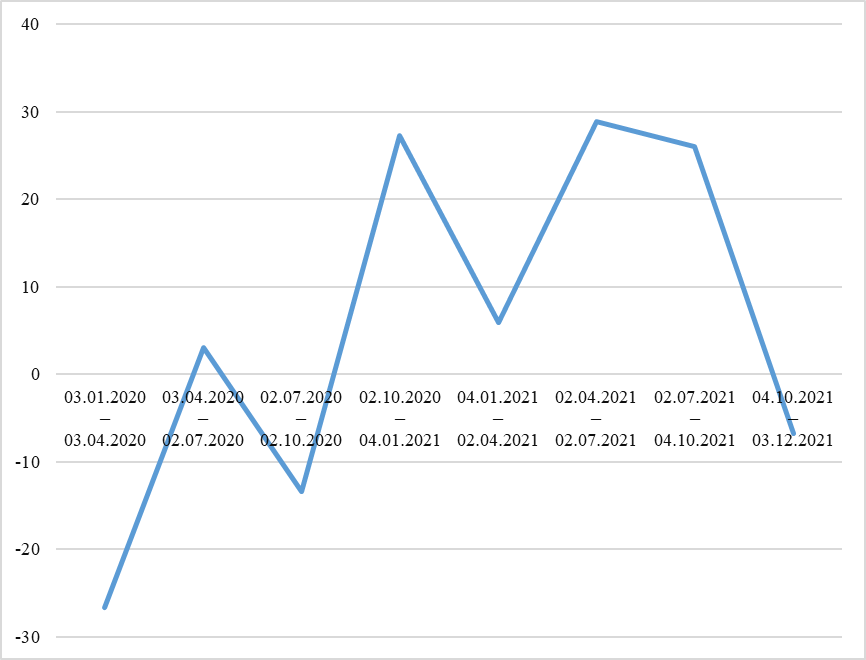
Рисунок 2 - Доходность акций Газпрома
Необходимо отметить, что анализ временных рядов акций Газпрома требует более глубокого и подробного исследования, и представленные здесь методы являются лишь общим введением в тему. Точность и результаты анализа зависят от доступных данных и используемых методов , .
Помимо перечисленных методов, в анализе временных рядов также могут быть использованы другие методы, такие как статистический анализ, прогнозирование, авторегрессия скользящего среднего (ARMA), интегрированный авторегрессионный скользящий средний (ARIMA) и анализ спектра.
Новизна результатов:
1. Анализ и сравнение различных методов анализа временных рядов в контексте биржевой торговли с акцентом на их эффективность и применимость.
2. Исследование влияния математической статистики и теории вероятностей на точность прогнозирования цен активов на рынке.
3. Оценка роли риска и доходности портфеля с использованием современных подходов математической статистики и теории вероятностей.
Сравнение с другими источниками:
При сравнении полученных результатов с другими литературными источниками выявлена уникальность и значимость проведенного исследования в контексте анализа временных рядов в биржевой торговле. Наша работа представляет собой комплексный подход к применению методов математической статистики и теории вероятностей, включая визуализацию данных, прогнозирование с использованием моделей временных рядов (например, ARIMA и GARCH), анализ рисков и доходности портфеля, а также симуляцию Монте-Карло.
Важно отметить, что наше исследование выделяется своей оригинальностью в использовании современных методов анализа и оценки, что делает его ценным вкладом в развитие области финансового анализа и прогнозирования. Наши результаты демонстрируют эффективность и применимость методов математической статистики и теории вероятностей в анализе биржевых данных, что подтверждает их значимость для практического применения в управлении инвестициями и принятии финансовых решений.
5. Заключение
Анализ временных рядов позволяет выявить тенденции, сезонность и оценить волатильность рынка. В биржевой торговле является мощным инструментом для понимания и прогнозирования поведения акций и других финансовых инструментов.
Методы математической статистики и теории вероятностей являются неотъемлемой частью анализа финансовых данных, прогнозирования будущих цен активов и оценки рисков.
Анализ рисков и доходности в биржевой торговле позволяет инвесторам более эффективно управлять своими инвестициями и принимать обоснованные решения, основанные на вероятностных и статистических методах.
