РАЗВИТИЕ И ПРИМЕНЕНИЕ МЕТОДА CFD DESIGNER В ЗАДАЧАХ АЭРОДИНАМИКИ ВЕТРОВЫХ ТУРБИН
РАЗВИТИЕ И ПРИМЕНЕНИЕ МЕТОДА CFD DESIGNER В ЗАДАЧАХ АЭРОДИНАМИКИ ВЕТРОВЫХ ТУРБИН
Аннотация
Статья посвящена научным исследованиям, направленным на развитие и применение метода CFD designer в задачах аэродинамики ветровых турбин в плоской и пространственной постановке. Научная новизна исследования обусловлена тем, что проблема теоретико-механического описания аэродинамических воздействий на объекты сложной геометрии, вращающиеся в потоке среды, до сих пор не решена, несмотря на ее актуальность, за исключением некоторых частных случаев, когда могут быть сделаны упрощающие предположения. В то же время такое описание позволяет создавать замкнутые динамические модели механических систем и проводить их параметрический анализ с помощью метода CFD designer. В данной работе с помощью метода CFD designer и параметрического моделирования были установлены функциональные зависимости между параметрами лопатки турбины и ее энергетическими показателями. Моделирование позволило выявить связи между объектом исследования и взаимодействующими факторами, такими как крутящий момент и зоны отрыва потока, угол атаки и коэффициенты лобового сопротивления. Аэродинамические профили турбин показали значительные улучшения по сравнению с исходными базовыми формами, поэтому методологический подход CFD designer может быть использован для расчетов характеристик ветровых турбин с объектами более сложной геометрии, вращающимися в потоке среды, например, для сочетания роторов Савониуса с роторами Дарье.
1. Введение
Одной из основных задач электроснабжения децентрализованных районов (труднодоступные горные районы, районы крайнего Севера) является задача обеспечения эффективного функционирования электрических систем совместно с возобновляемыми источниками энергии. Для получения максимальной производительности энергии ветра используются ветряные турбины. Ветряные турбины обычно классифицируются как турбины с горизонтальной или вертикальной осью в соответствии с положением их оси вращения. К настоящему времени проведено и проводится множество исследований по совершенствованию конструкционных и динамических параметров турбин . Оптимизация формы профиля является одним из основных этапов проектирования аэродинамических компонентов, таких как лопасти ветрогенераторов . Процесс оптимизации обычно включает три основных элемента: параметризацию формы, оценку формы и непосредственно саму оптимизацию. Для обеспечения эффективности метод параметризации должен охватывать большое пространство проектирования с небольшим количеством параметров, т.е. определять как пространство проектирования, так и сложность задачи оптимизации. Это особенно важно на начальном этапе проектирования, когда накладываются минимальные геометрические ограничения, а профили лопастей могут быть значительно изменены в процессе оптимизации.
2. Методы и принципы исследования
Оптимизация турбины с помощью методов параметризации формы основаны на тщательном выборе геометрических ограничений и параметров, что гарантирует высокую точность расчета. Точность, обеспечиваемая такими методами, в значительной степени зависит от количества выбранных параметров. Более того, все расчеты связаны параметрическими ограничениями, что затрудняет выполнение экстраполяции или внесение радикальных глобальных изменений. Методы, основанные на базе данных, обычно созданы в предположении, что оптимальные решения находятся вблизи от набора данных, что опять же ограничивает возможность радикального изменения формы.
По мере оптимизации геометрических характеристик каждого из параметров разрабатываются классические подходы, основанные на контурных кривых и контрольных точках. Например, в широко используемом методе параметрического моделирования (PARSEC) применяется полином шестого порядка для создания поверхности профиля, позволяющий исследовать несколько параметров, характеризующих аэродинамику профиля, таких как радиус передней кромки и положение верхнего и нижнего крыла. Другим распространенным методом является параметризация Безье , которая позволяет смоделировать верхнюю и нижнюю поверхности крыла с помощью кривых Безье, заданных предварительно выбранными контрольными точками. Одной из основных проблем вышеупомянутых методов является их неэффективность расчета очень чувствительных к нагрузкам характеристик. Эти методы имеют фиксированное число параметров и ограниченный диапазон точности. Кроме того, для параметризации Безье необходимо наличие кривых более высокого порядка для описания сложных форм, что приводит к ее неэффективности с вычислительной точки зрения .
Один из способов уменьшить количество параметров конструкции – сгруппировать контрольные точки таким образом, чтобы в качестве параметров можно было использовать глобальные преобразования, такие как кручение и утолщение лопастей. Этот метод известен как деформация свободной формы (FFD) . Аналогичный метод, называемый аппроксимацией радиальной базисной функцией (RBF) , также доступен для доменных элементов и использует RBF для деформации профиля.
Более глобальный подход заключается в деформации профиля с помощью спектральных базисных функций. Обычной базисной функцией является доминирующая модель, полученная в результате сингулярного разложения (Singular Value Decomposition, SVD) прямоугольной матрицы с целью ее приведения к каноническому виду заданного профиля. Существуют также синусоидальные функции в подходе Хикса-Хенне и поверхностные функции в методе преобразования функции класса/формы, выраженные как произведение функции класса и функции формы, полученной линейной комбинацией полиномов Бернштейна. Однако эти методы также зависят от размерности, и для получения высокоточных функций всегда требуется больше базисных функций и режимов.
В работе генеративные сети (GAN) использовались для изучения вариаций формы, лежащих в базе данных профилей, и для параметризации формы. Однако, как и во многих других методах, чем меньше размеры, тем ближе оптимальная форма лопасти к базе данных.
Для учета более тонких деталей формы лопасти или, эквивалентно, для представления более сложных кривых можно использовать B-сплайны , которые создают кривые путем объединения сегментов Безье низкого порядка, заданных контрольными точками. При увеличении числа контрольных точек эти методы смещаются к локальному краю, что позволяет представлять объекты с высокой точностью.
При всей эффективности последнего подхода, его применение в настоящее время технически трудно реализуемо из-за вычислительной сложности процесса. По этой причине обычно используется подход, основанный на численном решении осредненных по Рейнольдсу уравнений Навье-Стокса, и полуэмпирических моделях турбулентности. Точность вычислений и объем вычислительных итераций в данном случае зависят от способа моделирования пристенной области.
Следующий метод вычислительной гидродинамики (Computational fluid dynamic, CFD) позволяет решать вопросы тепло- и массопереноса в различных технических и природных объектах. Основной целью метода CFD является численное решение уравнений Навье-Стокса, но могут быть учтены, к примеру, турбулентность или потоки через проницаемую среду. В работе методы CFD используются для сравнения результатов экспериментов с CFD по оптимизации ротора ветротурбины.
3. Основные результаты
Для решения задачи по оптимизации аэродинамического профиля ветротурбины был использован метод параметрического моделирования CFD designer . У этого метода есть несколько преимуществ, среди которых возможность применения метода CFD для фигур любого размера и его способность создавать экзотические формы, поскольку можно комбинировать радикально отличающиеся базовые формы. Кроме того, CFD designer не накладывает никаких геометрических ограничений на параметры проектирования. И единственными неявными ограничениями являются сами варианты базовых фигур, которые необходимы для определения задачи, подлежащей решению. Наконец, метод CFD способен создать обширное пространство для поиска новой конструкции, даже среди малого количества известных конструкций.
Оптимизация формы аэродинамического профиля выполнена посредством управления пограничным слоем на лопастях турбины, что позволит исключить отрыв потока. Основой для моделирования является ротор Савониуса – конструкция с лопастями в виде цилиндрических поверхностей. Известен ротор Савониуса с полыми лопастями, содержащий цилиндрические лопасти, расположенные параллельно оси вращения ротора, где каждая лопасть выполнена полой с прорезями на ее продольных торцах для выхода воздуха (патент РФ RU 94 028 552 A1 от 1996.07.27.), который принят за прототип. Недостатками прототипа являются: снижение КПД из-за нестабильности работы, связанной с возникновением турбулентности (возникновение завихрений) в обдуваемом потоке воздуха, особенно при порывистом ветре, что ограничивает предел эффективного использования. Согласно изобретению, лопасти турбины снабжены вихревыми генераторами, что приводит к увеличению максимального коэффициента подъемной силы за счет уменьшения вероятности отрыва потока над лопастью и позволяет лопасти работать с большим углом атаки при различных значениях лобового сопротивления. Величина максимального коэффициента подъемной силы лопасти, как правило, будет зависеть от конструкции вихревых генераторов, количества последовательных их рядов, а также конструкции профиля самой лопасти. Ряды вихревых генераторов могут быть установлены в любом положении лопасти в зависимости от ее конструкции и аэродинамических свойств. Благодаря высокому коэффициенту подъемной силы имеется возможность уменьшить необходимую площадь лопасти и нагрузку, либо увеличить длину лопасти и сохранить первоначальную нагрузку при более высокой производительности.
Ранее расчет установившегося течения известного профиля Савониуса проводился в рамках потенциального приближения с использованием численных процедур, разработанных исключительно для этого приближения. В данной работе расчет был сделан в рамках метода CFD designer. В результате моделирования получены оптимальные геометрические размеры ротора. Результатом данного моделирования являются не только точные параметры потока, но и аэродинамическое поведение ротора. Результаты сравниваются с экспериментальными данными прототипа. В частности, возможно прогнозирование аэродинамических моментов для нескольких геометрических конфигураций.

Рисунок 1 - Форма аэродинамического профиля в исходном и оптимизированном виде
В случае с коэффициентом лобового сопротивления, зазор между углом атаки подъемной силы и расчетной точкой составляет 8°, что обеспечивает аэродинамическому профилю широкий допустимый диапазон для операций, не связанных с решением конкретной задачи, что показано на рисунке 2.
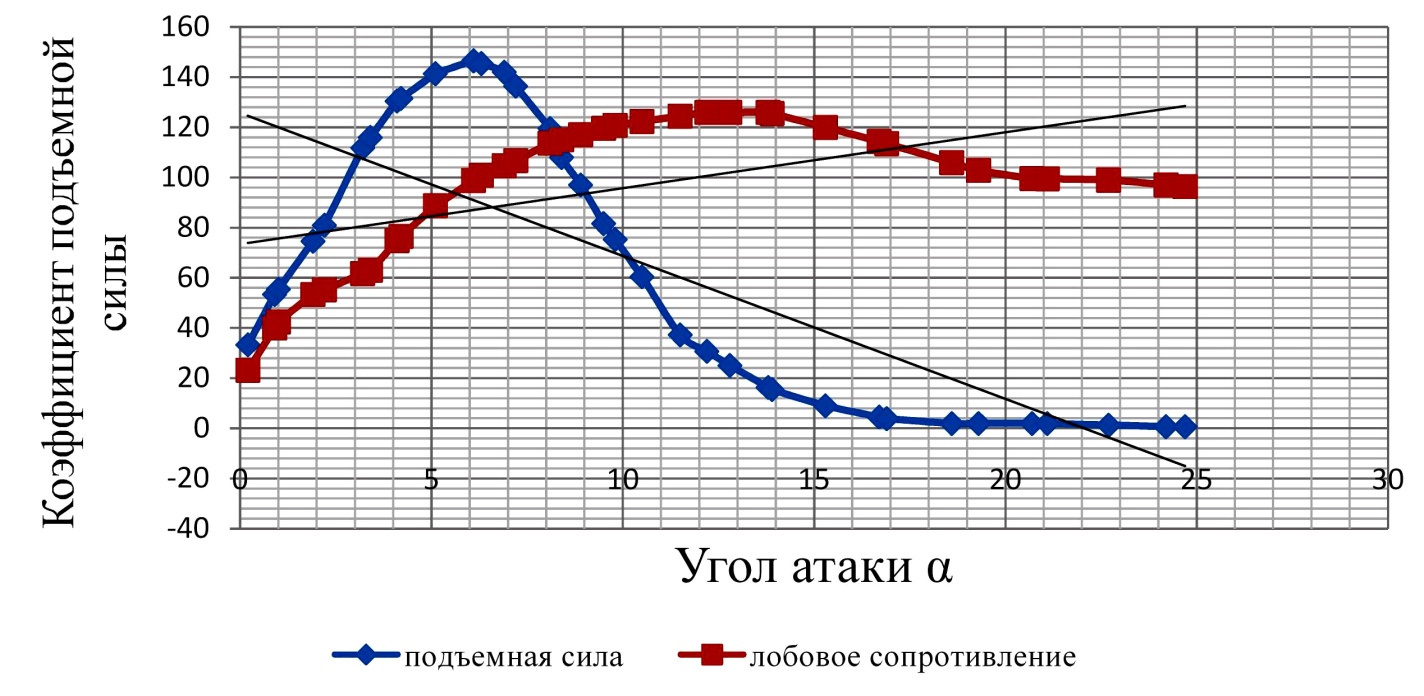
Рисунок 2 - Зависимость подъемной силы лопатки от угла атаки при различных значениях лобового сопротивления
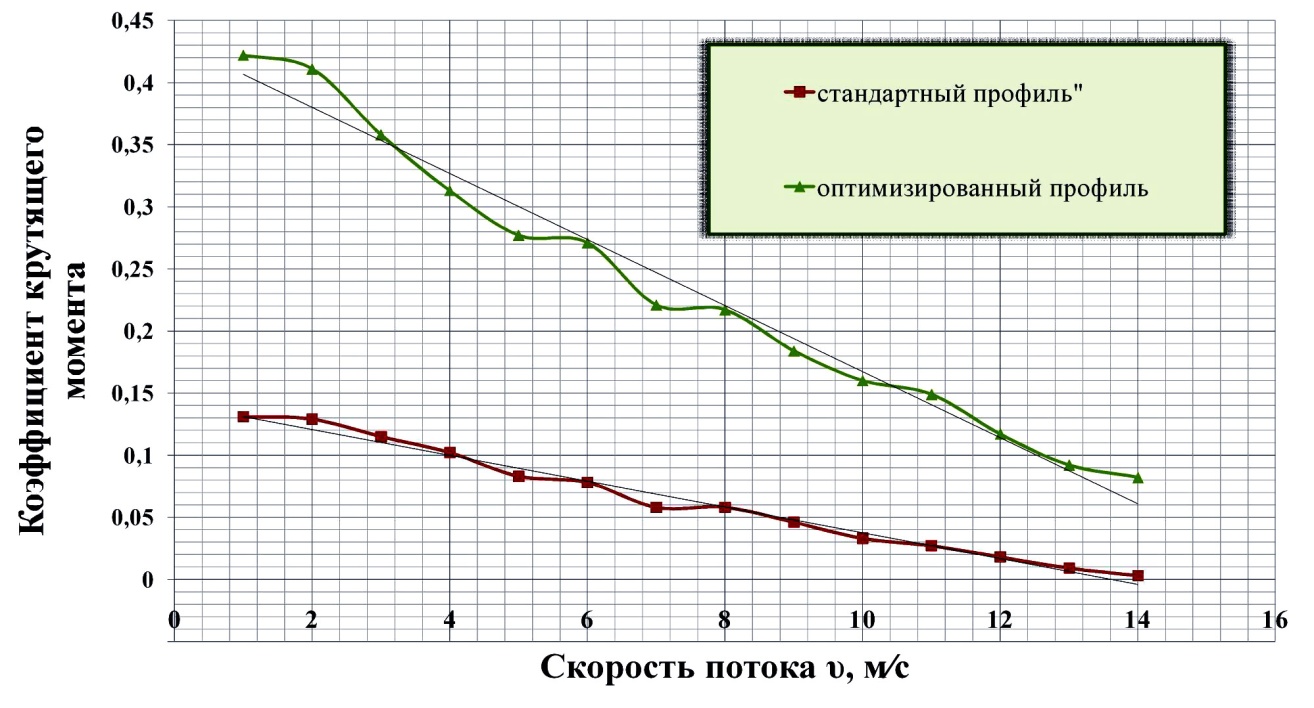
Рисунок 3 - Сравнение характеристик стандартного и спроектированного профиля
4. Заключение
1. Проведено научное исследование применения методов CFD- designer в аэродинамике ветровых турбин в плоской и пространственной постановках. Метод CFD designer был использован для оптимизации аэродинамического профиля ветряных турбин путем установления функциональных зависимостей между параметрами лопаток турбины и показателями ее энергетической эффективности.
2. Выявлена взаимосвязь между исследуемым объектом и взаимодействующими факторами, такими как крутящий момент, зона разделения, угол атаки и коэффициент сопротивления. Аэродинамический профиль турбины был значительно улучшен по сравнению с первоначальной базовой геометрией. Таким образом, метод CFD- designer может быть использован для расчета характеристик ветротурбин с более сложной геометрией, в частности для сочетания ротора Савониуса с роторами Дарье.
3. Благодаря высокому коэффициенту подъемной силы имеется возможность уменьшить необходимую площадь лопасти и нагрузку или увеличить длину лопастей для достижения более высокой производительности при сохранении исходной нагрузки. Кроме того, сфера исследований может быть расширена и включать в себя гибридные энергетические системы с другими возобновляемыми источниками энергии. Это позволит создать интеграцию таких технологий, как гидроэнергетика и геотермальная энергия, для реализации более надежных и устойчивых энергетических систем.
4. Проведен сравнительный анализ производительности исследуемой ветротурбины с аналогичными исследованиями стандартного ротора Савониуса с использованием математической модели, показавшее улучшение аэродинамических характеристик по сравнению с её исходными базовыми значениями.
