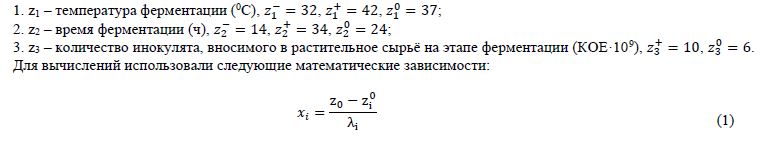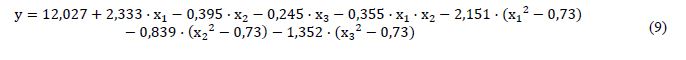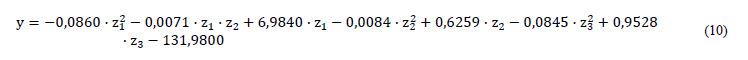МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ НАКОПЛЕНИЯ ПОЛИСАХАРИДОВ В БИОМАССЕ ЛИСТЬЕВ A. LAPPAL. В ПРОЦЕССЕ МИКРОБНОЙ ФЕРМЕНТАЦИИ

DOI: https://doi.org/10.23670/IRJ.2022.118.4.105

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ НАКОПЛЕНИЯ ПОЛИСАХАРИДОВ В БИОМАССЕ ЛИСТЬЕВ A. LAPPAL. В ПРОЦЕССЕ МИКРОБНОЙ ФЕРМЕНТАЦИИ

Научная статья

Хайбуллин Р.Г.^{1, *}, Волкова Л.В.²

^{1, 2}Пермский национальный исследовательский политехнический университет, Пермь, Россия

^* Корреспондирующий автор (ruslan.khaibullin[at]yandex.ru)

Аннотация

Одним из способов повышения эффективности процесса ферментации растительного сырья является введение пробиотических микроорганизмов в реакционную среду, что позволяет обогатить продукт бактериальными метаболитами, в т.ч. экзополисахаридами. Перспективным сырьём для получения биологически активных субстанций является ArctiumlappaL. (лопух большой), содержащий в своём составе полисахарид инулин, оказывающий гипогликемический эффект на организм человека. В результате проведённых экспериментов, для дальнейших расчётов оптимальных параметров проведения процесса, получена математическая зависимость накопления полисахаридов в процессе микробной ферментации биомассы листьев A. lappaL.

Ключевые слова: A. lappaL., микробная ферментация,Lactobacillusplantarum, математическое моделирование, полисахариды.

MATHEMATICAL MODELING OF THE ACCUMULATION OF POLYSACCHARIDES IN THE BIOMASS OF LEAVES A. LAPPA L. IN THE PROCESS OF MICROBIAL FERMENTATION

Research article

Khaybullin R.G.^{1, *}, Volkova L.V.²

^{1, 2} Perm National Research Polytechnic University, Perm, Russia

^* Corresponding author (ruslan.khaibullin[at]yandex.ru)

Abstract

One of the ways to increase the efficiency of the fermentation process of plant raw materials is the introduction of probiotic microorganisms into the reaction medium, which makes it possible to enrich the product with bacterial metabolites, including exopolysaccharides. A promising raw material for the production of biologically active substances is Arctium lappa L. (greater burdock) with the polysaccharide inulin in its composition, which has a hypoglycemic effect on the human body. As a result of the experiments, for further calculations of the optimal parameters of the process, a mathematical dependence of the accumulation of polysaccharides in the process of microbial fermentation of A. lappa L. leaf biomass was obtained.

Keywords: A. lappa L., microbial fermentation, Lactobacillus plantarum, mathematical modeling, polysaccharides.

Введение

Биомасса лопуха большого (ArctiumlappaL.)содержит ряд биологически активных веществ (БАВ), таких как дубильные вещества, тритерпеноиды, аргинин, фитостерины, рутин, кверцетин, а также водорастворимые полисахариды, в т.ч. инулин. [1], [2], [5], [6]. В настоящее время ферментация растительного сырья получила широкое применение в производстве лекарственных препаратов и биологически активных добавок (БАД). [7], [8]. «В качестве одного из подходов к получению эффективных растительных препаратов и введению в них дополнительных свойств может рассматриваться ферментация биомассы растений при помощи пробиотических микроорганизмов рода Lactobacillus» [8, С. 6]. Микробная ферментация позволит получить ферментированную растительную субстанцию, обогащённую продуктами бактериального метаболизма, такими как экзополисахариды, короткоцепочечные жирные кислоты, аминокислоты и др. [8].

Необходимость получения математической модели и дальнейшей оптимизации технологических параметров проведения процесса микробной ферментации обусловлена целью получения более ценного по своему составу растительного продукта.

Методы исследования

С целью установления математической зависимости накопления полисахаридов в ферментируемом продукте в процессе проведения микробной ферментации биомассы листьев A. lappa L., был поставлен ряд исследований по плану ортогонального центрального композиционного эксперимента 2³. В качестве выходных данных использовался показатель количества полисахаридов, учитывающий как присутствующий в сырье инулин, так и синтезируемые в процессе ферментации экзополисахариды. В качестве факторов, влияющих на качество конечного продукта, были установлены:

Для вычислений использовали следующие математические зависимости:

Ферментацию растительного сырья проводили согласно методике, описанной в патенте на изобретение RU 2019 119 049 A [9], сырьё брали в количестве 100 г. В качестве инокулята использовали микроорганизмы вида Lactobacillusplantarum, полученные из препарата «Лактобактерин сухой лиоф. 5 доз фл. №10» (АО «Микроген» «Пермское НПО Биомед»), содержащего микробную биомассу L. plantarum в количестве 2∙10⁹ КОЕ на 1 дозу. Количественный анализ полисахаридов проводили по методике, описанной в ФС.2.5.0025.15 [10].

Экспериментальная часть

На начальном этапе осуществили пересчёт натуральных значений факторов (z_i) в кодированные (x_i) по формуле (1), где  - центр плана 2³,  - интервал варьирования изучаемых факторов (Таблица 1).

Таблица 1 – Кодирование исследуемых факторов

Фактор					Переход к кодированным переменным
z1	42	37	32	5
z2	34	24	14	10
z3	10	6	2	4

В соответствии с выбранным типом планирования, составили матрицу, включающую в себя 8 опытов полного факторного эксперимента, 6 опытов в «звёздных точках» и 1 опыт в центре плана (Таблица 2). Согласно ядру плана 2³, значение «звёздного плеча» (α) составило 1,215, константа преобразования (β) = 0,73. Значения взаимодействующих факторов x₄-x₆ рассчитывали по формуле (2).

Таблица 2 – Матрица планирования эксперимента 2³

№	x0	x1	x2	x3	x1x2	x1x3	x2x3	x1x2x3	x4	x5	x6
1	1	-1	-1	-1	1	1	1	-1	0,27	0,27	0,27
2	1	1	-1	-1	-1	-1	1	1	0,27	0,27	0,27
3	1	-1	1	-1	-1	1	-1	1	0,27	0,27	0,27
4	1	1	1	-1	1	-1	-1	-1	0,27	0,27	0,27
5	1	-1	-1	1	1	-1	-1	1	0,27	0,27	0,27
6	1	1	-1	1	-1	1	-1	-1	0,27	0,27	0,27
7	1	-1	1	1	-1	-1	1	-1	0,27	0,27	0,27
8	1	1	1	1	1	1	1	1	0,27	0,27	0,27
9	1	-1,215	0	0	0	0	0	0	0,75	-0,73	-0,73
10	1	1,215	0	0	0	0	0	0	0,75	-0,73	-0,73
11	1	0	-1,215	0	0	0	0	0	-0,73	0,75	-0,73
12	1	0	1,215	0	0	0	0	0	-0,73	0,75	-0,73
13	1	0	0	-1,215	0	0	0	0	-0,73	-0,73	0,75

Окончание таблицы 2 – Матрица планирования эксперимента 2³

№	x0	x1	x2	x3	x1x2	x1x3	x2x3	x1x2x3	x4	x5	x6
14	1	0	0	1,215	0	0	0	0	-0,73	-0,73	0,75
15	1	0	0	0	0	0	0	0	-0,73	-0,73	-0,73
	15	10,952	10,952	10,952	8	8	8	8	4,373	4,373	4,373

Исходя из составленной матрицы планирования, провели ряд исследований и получили экспериментальные данные. Вычислили средние выборочные результатов экспериментов (3), где m – количество повторностей, n – общее количество экспериментов, построили матрицу планирования 2³ для обработки данных (Таблица 3).

Таблица 3 – Матрица планирования 2³ для обработки результатов

№	x1	x2	x3	y1	y2	y3
1	32	14	2	8,94	8,92	8,68	8,85
2	42	14	2	14,09	14,11	14,01	14,07
3	32	34	2	8,91	8,79	8,72	8,81
4	42	34	2	12,62	12,51	12,56	12,56
5	32	14	10	8,42	8,45	8,41	8,43
6	42	14	10	13,47	13,52	13,65	13,55
7	32	34	10	8,36	8,31	8,27	8,31
8	42	34	10	11,95	12,08	12,14	12,06
9	30,925	24	6	9,38	9,31	9,29	9,33
10	43,075	24	6	14,75	14,81	14,74	14,77
11	37	11,85	6	14,35	14,49	14,57	14,47
12	37	36,15	6	13,57	13,43	13,50	13,50
13	37	24	1,14	13,52	13,50	13,58	13,53
14	37	24	10,86	12,87	12,95	12,94	12,92
15	37	24	6	15,36	15,17	15,24	15,26

По экспериментальным результатам произвели расчёт коэффициентов уравнения регрессии (4). Вычислили дисперсию воспроизводимости  (5) и среднее квадратичное отклонение полученных коэффициентов (6). Исходя из числа степеней свободы n= 30, уровня значимости α = 0,05, по таблицам распределения Стьюдента нашли t_кр и установили значение t_кр·  (Таблица 4).

Таблица 4 – Расчет дисперсий и коэффициентов уравнения регрессии

№													tкр				tкр·
1	0,009			0,005		0,028			0,021		0,006		2,042		0,012		0,024
2	0,000			0,002		0,004			0,003
3	0,011			0,000		0,008			0,009
4	0,003			0,003		0,000			0,003
5	0,000			0,001		0,000			0,000
6	0,006			0,001		0,011			0,009
7	0,002			0,000		0,002			0,002
8	0,011			0,001		0,007			0,009
9	0,003			0,000		0,001			0,002
10	0,000			0,002		0,001			0,001
11	0,014			0,000		0,010			0,012
12	0,005			0,005		0,000			0,005
13	0,000			0,001		0,002			0,002
14	0,003			0,001		0,000			0,002
15	0,011			0,008		0,000			0,009
Полученные коэффициенты уравнения регрессии
b0		b1	b2		b3		b12	b13		b23		b123		b4		b5		b6
12,027		2,233	-0,395		-0,245		-0,355	-0,015		-0,007		0,011		-2,151		-0,839		-1,352

Сравнивая значения t_кр·  с коэффициентами уравнения регрессии, установили их значимость, принимая во внимание, что коэффициент является значимым в случае выполнения неравенства |b_n|>t_кр· . По результатам анализа, коэффициенты b₁₃, b₂₃ иb₁₂₃ оказались меньше значения t_кр· . Таким образом, уравнение регрессии в кодированных переменных приняло вид (9):

Полученное уравнение регрессии (9) оценили на адекватность по критерию Фишера. Нашли расчётные значения функции отклика (y_{i расч}) (9), вычислили дисперсию адекватности  (7), где r– число значимых коэффициентов уравнения, далее определили расчётное значение критерия Фишера (F_расч) (8). Табличное значение (F_табл) нашли по таблицам распределения Фишера при уровне значимости α=0,05 и степеням свободы: k₁=7иk₂=30. На основании параметра F_табл провели оценку уравнения регрессии (9), учитывая его адекватность в случае выполнения неравенства F_расч.<F_табл.(Таблица 5).

Таблица 5 – Проверка полученного уравнения на адекватность

№	yi расч		Fрасч	Fтабл	Адекватность
1	8,91	0,0078	1,303	2,330	Уравнение регрессии адекватно
2	14,08
3	8,83
4	12,58
5	8,42
6	13,59
7	8,34
8	12,09
9	9,30
10	14,73
11	14,44
12	13,47
13	13,49
14	12,90
15	15,20

Далее, преобразовали кодированное уравнение регрессии (9) в натуральных переменных (10):

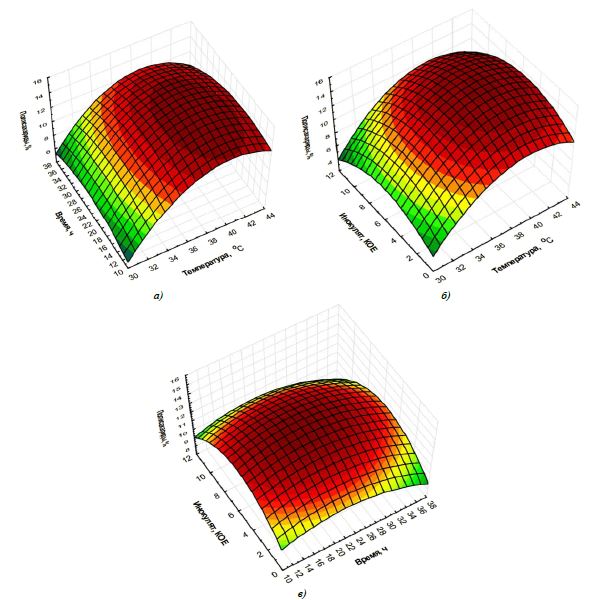
При помощи программного обеспечения (ПО) «Statisticav.10» (StatSoft) построили графики зависимостей количества полисахаридов в ферментированном продукте от изучаемых технологических факторов (Рисунок 1).

Рис. 1 – Зависимости исследуемых технологических факторов от количества полисахаридов в получаемых продуктах: а)T (°С), τ (ч); б)T (°С), кол-во клеток (КОЕ∙10⁹), в)τ (ч), инокулят (КОЕ∙10⁹)

Как видно из полученных зависимостей, при температуре, превышающей оптимальную температуру роста L. plantarum, накопление полисахаридов происходит с меньшей интенсивностью, т.к. культура перестраивает процессы своего метаболизма, сокращает процессы биосинтеза вторичных метаболитов и потребляет больше ресурсов, в т.ч. имеющиеся полисахариды растительного сырья, с целью повышения своей выживаемости. При внесении в реакционную среду большого количества инокулята, наступает период быстрого клеточного роста, ввиду чего развивающимся клеткам становится недостаточно ресурсов, и колония не синтезирует достаточного количества метаболитов, потребляя имеющиеся питательные вещества растительного сырья. При длительной продолжительности процесса ферментации происходит потребление БАВ сырья растущей колонией. В случае воздействия технологических факторов, имеющих значения ниже оптимальных, процессы роста, развития клеток и биосинтеза БАВ также проходят значительно медленнее.

Заключение

Было изучено влияние температуры (°С), времени (ч) и количества вносимого инокулята (КОЕ) на количество полисахаридов, образующихся в процессе микробной ферментации биомассы листьев A. lappaL, получена математическая модель и диаграммы зависимостей технологических факторов от функции отклика. Дальнейшая оптимизация процесса микробной ферментации биомассы листьев A. lappaL должна учитывать комплексный анализ дополнительных функций отклика, таких как количество экстрактивных веществ, дубильных веществ, кислот-метаболитов и других.

Конфликт интересов	Conflict of Interest
Не указан.	None declared.

 

Список литературы / References

1. Фенольные соединения листьев лопуха / А.А. Савина, В.И. Шейченко, А.Л. Петрова и др. // Вопросы биологической, медицинской и фармацевтической химии. – 2013. – 1 – pp. 9-13;
2. Identification of a dicaffeoylquinic acid isomer from Arctium lappa with a potent anti-ulcer activity / Carlotto J., da Silva L.M., Dartora N. et al.– Talanta, 2015. – Apr., 135. – pp. 50-57.
3. Jeelani S.Triterpenoids from Arctium lappa / Jeelani, M.A. Khuroo // Natural product research. – 2012. – 26(7). – pp. 654-658.
4. A review of the pharmacological effects of Arctium lappa (burdock) / Chan Y.S., Cheng L.N., Wu J.H. et al. // Inflammopharmacology. – 2011. – Oct.; 19(5) – pp. 245-254;
5. Biologically active fructan from the roots of Arctium lappa, var. Herkules / A. Kardosova, A. Ebringerova, J. Alfoldi, et al. // International journal of biological macromolecules. – 2003. – Nov.; 33(1-3). – pp. 135-140.
6. Sychev I.A.Study of composition, physical and chemical properties and biological activity of polysaccharide complex of Arctium lappa leaves / I.A. Sychev, D.G. Kokina // IP Pavlov Russian Medical Biological Herald. – 2017. – 25(1). – pp. 42-48.
7. Терёшина Н.С.Ферментация и получение лекарственных препаратов / Н.С. Терёшина, И.А. Самылина, З.П. Костенникова // Фармация. – 2012. – 3. – pp. 53−56.
8. Хайбуллин Р.Г.Перспективы получения биологически активных субстанций из биомассы растений методом микробной ферментации (обзор) / Р.Г. Хайбуллин, Л.В. Волкова // Вопросы биологической, медицинской и фармацевтической химии. – 2021. – 4. – pp. 3−12.
9. Патент № 2733141 (РФ). Способ получения фитокомпозиции/ Волкова Л.В., Хайбуллин Р.Г.; заявитель и патентообладатель Пермский национальный исследовательский политехнический университет. – № 2019119049: заявл. 18.06.2019: опубл. 29.09.2020.– 6 с.
10. ФС.2.5.0025.15 Лопуха корни // Фармакопея.рф : [Электронный ресурс]. — URL: https://pharmacopoeia.ru/fs-2-5-0025-15-lopuha-korni/ (дата обращения: 25.11.2021).

Список литературы на английском языке / References in English

1. Fenol'nye soedinenija list'ev lopuha [Phenoliccompoundsofburdockleaves] / A.A. Savina, V.I. Shejchenko, A.L. Petrova et al. // Voprosy biologicheskoj, medicinskoj i farmacevticheskoj himii [Problems of biological medical and pharmaceutical chemistry] – 2013; 1: 9-13; [in Russian]
2. Identification of a dicaffeoylquinic acid isomer from Arctium lappa with a potent anti-ulcer activity / Carlotto J., da Silva L.M., Dartora N. et al. – Talanta, 2015. – Apr., 135. – pp. 50-57.
3. Jeelani S. Triterpenoids from Arctium lappa / Jeelani, M.A. Khuroo // Natural product research. – 2012. – 26(7). – pp. 654-658.
4. A review of the pharmacological effects of Arctium lappa (burdock) / Chan Y.S., Cheng L.N., Wu J.H. et al. // Inflammopharmacology. – 2011. – Oct.; 19(5) – pp. 245-254;
5. Biologically active fructan from the roots of Arctium lappa, var. Herkules / A. Kardosova, A. Ebringerova, J. Alfoldi, et al. // International journal of biological macromolecules. – 2003. – Nov.; 33(1-3). – pp. 135-140.
6. Sychev I.A. Study of composition, physical and chemical properties and biological activity of polysaccharide complex of Arctium lappa leaves / I.A. Sychev, D.G. Kokina // IP Pavlov Russian Medical Biological Herald. – 2017. – 25(1). – pp. 42-48.
7. Terjoshina N.S. Fermentacija i poluchenie lekarstvennyh preparatov [Fermentation and drug preparation] / S. Terjoshina, I. A. Samylina, Z. P. Kostennikova // Farmacija [Pharmacy]. 2012. –3. –pp. 53−56. [in Russian]
8. Khaibullin R.G. Perspektivy poluchenija biologicheski aktivnyh substancij iz biomassy rastenij metodom mikrobnoj fermentacii (obzor) [Perspectives for production plant biomass biologically active product by the microbial fermentation method (review)] / R.G. Khaibullin, L.V. Volkova // Voprosy biologicheskoj, medicinskoj i farmacevticheskoj himii. [Problems of biological medical and pharmaceutical chemistry] – 2021. – 4 – pp. 3−12; [in Russian]
9. № 2733141 Russian Federation. Sposob poluchenija fitokompozicii / Volkova L.V., Hajbullin R.G.; The applicant and the patentee Perm national research polytechnic university – № 2019119049: appl. 06/18/19: publ. 29.09.20. – 6 p. [in Russian]
10. 2.5.0025.15 Lopuha korni. [Pharmacopoeia article 2.5.0025.15 Burdock roots] // Farmakopeja.rf: [Electronic resource]. — URL: https://pharmacopoeia.ru/fs-2-5-0025-15-lopuha-korni/ (accessed: 14.03.2022). [in Russian]