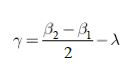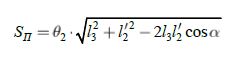АНАЛИЗ КРИТЕРИЕВ ОПТИМАЛЬНОСТИ ДВИЖЕНИЯ РАБОЧЕГО ОРГАНА ПЕРЕМЕШИВАЮЩЕГО МЕХАНИЗМА

DOI: https://doi.org/10.23670/IRJ.2022.118.4.018

АНАЛИЗ КРИТЕРИЕВ ОПТИМАЛЬНОСТИ ДВИЖЕНИЯ РАБОЧЕГО ОРГАНА ПЕРЕМЕШИВАЮЩЕГО МЕХАНИЗМА

Научная статья

Чусовитин Н.А.^1,*,Чусовитин Г.Н.²

¹ ORCID: 0000-0002-0055-5036;

²ORCID: 0000-0003-0367-584X;

^{1, 2} Новосибирский Государственный Технический Университет, Новосибирск, Россия

^* Корреспондирующий автор (choos328[at]mail.ru)

Аннотация

Предлагаемое устройство относится к пространственным винто–рычажным механизмам и может быть использовано в пищевой, медицинской, химической, строительной отраслях промышленности, а также в сельском хозяйстве, как устройство, необходимое для приготовления однородных сред, позволяющее интенсифицировать массо- и теплообменные процессы, выравнивать концентрацию и температуру во всем объеме перемешиваемых веществ путем увеличения поверхности контакта фаз, обеспечить равномерное распределение энергии в объеме аппарата.

В сельском хозяйстве процесс перемешивания используют при приготовлении различных жидких удобрений, повышающих плодородие посевных площадей, многокомпонентных ядохимикатов для протравливания семян перед посевом; в химико-фармацевтической и медицинской промышленности - при приготовлении лекарственных веществ; в пищевой промышленности, например, при приготовлении сырных масс (V. Guileta, N. Chusovitin. Dispositis de mélange: diplôme d`une médaille d`or. Concours Lépine le salon Europeen de l’invention de Strasbourg. – Strasbourg, 2011), в кондитерском производстве – в целях замещения монотонных ручных операций; в машиностроении – при изготовлении шлифовальных кругов; в строительной индустрии – при производстве тонкокерамических изделий.

Несмотря на то, что большинство конструкций используемых механических перемешивающих устройств создавалось на основе практического опыта без достаточного обоснования, они являются в мировой практике доминирующим типом. Данный факт объясняется универсальностью таких аппаратов, надежностью их конструкций, высоким КПД по сравнению с перемешивающими устройствами других типов.

Ключевые слова: пространственный винто-рычажный механизм, критерии оптимальности движения рабочего органа.

An Analysis of the Optimality Criteria for the Movement of the Working Body of a Mixing Mechanism

Research article

Chusovitin N. A.^{1, *}, Chusovitin G.N.²

¹ ORCID: 0000-0002-0055-5036;

² ORCID: 0000-0003-0367-584X;

^{1, 2} Novosibirsk State Technical University, Novosibirsk, Russia

^* Corresponding author (choos328[at]mail.ru)

Abstract

The device proposed in this article relates to spatial lever-screw mechanisms and can be used in the food, medical, chemical, construction industries, as well as in agriculture, as a device necessary for the preparation of homogeneous media, allowing for intensifying mass and heat exchange processes, equalize the concentration and temperature in the entire volume of mixed substances by increasing the contact surface phases, to ensure an even distribution of energy in the volume of the apparatus.

In agriculture, the mixing process is used in the preparation of various liquid fertilizers that increase the fertility of cultivated areas, multicomponent pesticides for etching seeds before sowing; in the chemical, pharmaceutical and medical industries such as the preparation of medicinal substances; in the food industry – in the preparation of cheese curds (V. Guileta, N. Chusovitin. Dispositis de mélange: diplôme d`une médaille d`or.  Concours Lépine le salon Europeen de l’invention de Strasbourg. – Strasbourg, 2011), in confectionery production – in order to replace monotonous manual operations; in mechanical engineering – in the manufacture of grinding wheels; in the construction industry – in the production of fine ceramic products.

Despite the fact that most of the designs of the mechanical mixing devices used were created on the basis of practical experience without sufficient justification, they dominate in the world practice. This fact is explained by the versatility of such devices, the reliability of their designs, and high efficiency compared to mixing devices of other types.

Keywords: spatial lever-screw mechanism, criteria for optimal movement of the working organ.

Введение

Анализ существующих механических перемешивающих устройств пока­зал, что уменьшение застойных зон за счет увеличения размеров рабочего ор­гана, скорости его вращения и секционирования объемов перемешивания нельзя признать рациональным [1]. В связи с чем наилучшим решением представляется адресное перемещение рабочего органа в проблемную зону с непрерывным воздействием на перемешиваемый материал. При этом варьирование скорости вращения рабочего органа создает дополнительную турбулентность в смешиваемых материалах, и как следствие, позволяет увеличить их однородность, сократить время технологического процесса и энергозатраты.

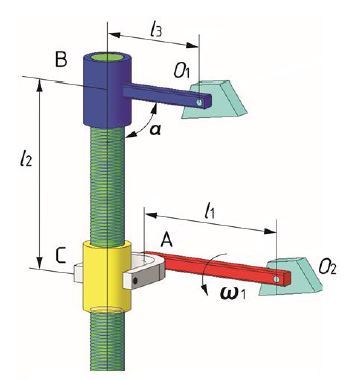
Указанным качествам в полной мере удовлетворяет пространственный механизм (патент РФ 2478473 B28C5/16 рис. 1), образованный минимальными числами низших кинематических пар {О₂, А-C, B, О₁} и простыми звеньями {О₂А, ВС,О₁В,О₁О₂}, имеющими длины l₁, l₂,l₃sinαи l₀, соответственно, где α – настроечный угол, определяющий взаимное положение звеньев 2 и 3.

Рис. 1 – Схема механизма

Перемешивание материалов реализуется вращением рабочего органа, соединенного с консолью звена 2, с угловыми скоростями φ¢₂₂ и φ¢₂ вокруг оси ВС и стойки О₁,соответственно. Совмещение движений ведущего звена механизма, при минимальном количестве кинематических пар и звеньев, является резервом для сокращения времени цикла и повышения производительности механизма.

Если размер коромысла l₃ отличен от нуля, траектория движения вершины L, представленная дугойL_ЛL_П окружности радиусом ,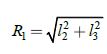

 не симметрична оси OY, где l₂ – минимально возможный размер винта, обеспечивающий существование механизма (рис. 2). Следовательно, проекции вершины винта в крайних положениях на данную ось будут различны. А значит, взаимное расположение механизма и реактора с горизонтальным или эллиптическим дном, следует признать нерациональным [1], [2],[3], в связи с тем, что погружение рабочего органа, связанного с консольной частью винта, в среду перемешивания в крайних положениях механизма различается, что приведёт к образованию застойных зон.

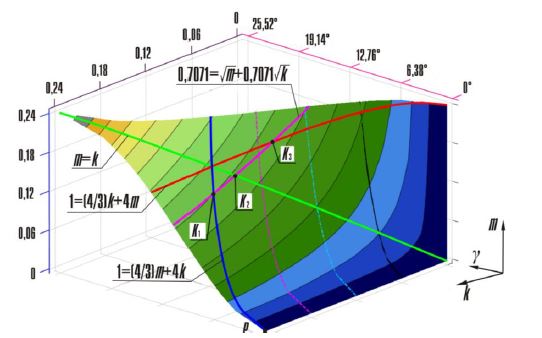
С целью подбора рациональных размеров реактора (емкости для перемешивания), определён угол коррекции γ, обеспечивающий приведение линии сим­метрии сектора с углом q₂ качания винта к вертикальной плоскости, что позволяет уменьшить динамические нагрузки на механизм и энергозатраты, а также распределить энергию рабочего органа симметрично оси реактора.

Угол коррекции γ равен углу между перпендикуляром к хорде, построенной на дуге перемещения вершины L винта и стойкой О₁О₂ и может быть реализован поворотом механизма относительно опоры О₁ по направлению движения часовой стрелки (рис. 2)

где b₁ и b₂ – углы между кривошипом в его крайних положениях и горизонтальной осью и их сумма есть не что иное как угол перекрытия θ₂ , R – перемещение вершины L кулисы,

Рис. 2 – Крайние положения механизма с выделением вертикального H и горизонтального R перемещений вершины L

Для упрощения решения и возможного обобщения результатов задачи метрического синтеза, заключающейся в определении значений геометрических параметров механизма, введена относительная система координат kОm, где

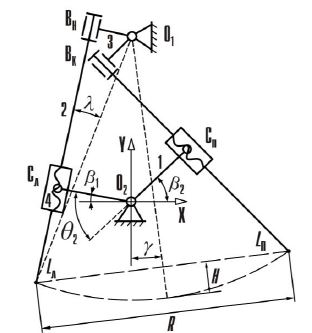
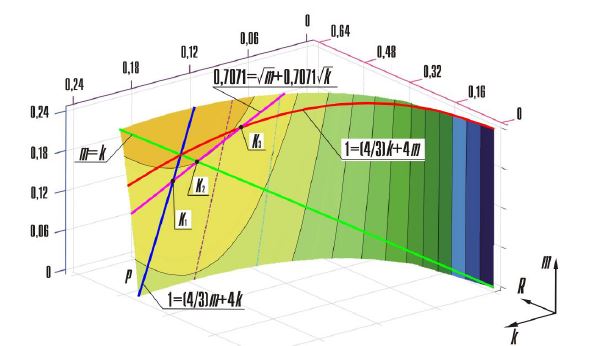
Рис. 3– Поверхность функции угла коррекции g = f(k,m) механизма

Отметим, что угол коррекции механизма достигает значения g_max»12^°при максимальном рекомендованном значении угла перекрытия q₂ =60° и реализуется в механизмах, синтезированных по координатам точки К₁(0,1988; 0,1536), принадлежащей области Е′,когда l₁>l₃, а также по координатам характерных точек К₂(0,1713; 0,1713)области Е1′ и К₃(0,1266; 0,2080) области Г1′ (рис.3).

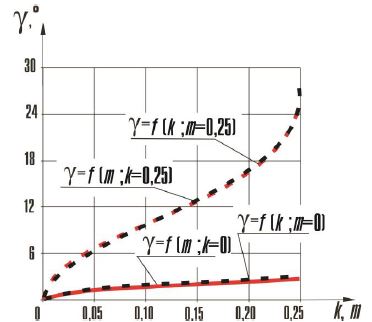
Рис. 4 – Графики функций γ=f(k) и γ=f(m)

Для разграничения степени влияния величины кривошипа и коромысла проведено поочередное исследование функции угла коррекции в зависимостиот одного параметра: от параметра k, или m, при фиксированном m=0 и 0,25, или при k=0 и 0,25, соответственно. В результате установлено равнозначное влияние на значение функции угла коррекции, параметра k или m при указанных условиях (рис. 4).

В корректированном положении механизма максимальные перемещения рабочего органаR (рис. 5)

равные стягивающей хорде центрального сектора (размах) на опорном угле q₂ реализуются, если длины звеньев удовлетворяют координатам К₂, когда k=m [5], [6].

Рис. 5– Поверхность функции перемещений R =f(R₁,θ₂), вершины винтаL

Для оценки производительности механизма введены критерии опти­мальности движения рабочего органа h и Н, равные отношению значений относительной угловой скорости φ¢₂₂ и переносной φ¢₂ к соответствующим путям S рабочего органа на прямых и обратных ходах звена 2 [7-9]. Путь рабочего органа при реализации переносного движения, отсчитываемый от крайнего левого до крайнего правого положения винта 2, проходит по дуге, величина которой определяется как:

гдеl^/₂ – габаритный размер звена 2, θ₂ – угол перекрытия равный углу кача­ния звена 2 относительно стойки О₁ (согласно рекомендации 0^°<θ₂ ≤60^°).

В относительном движении, путь кромки рабочего органа равен:

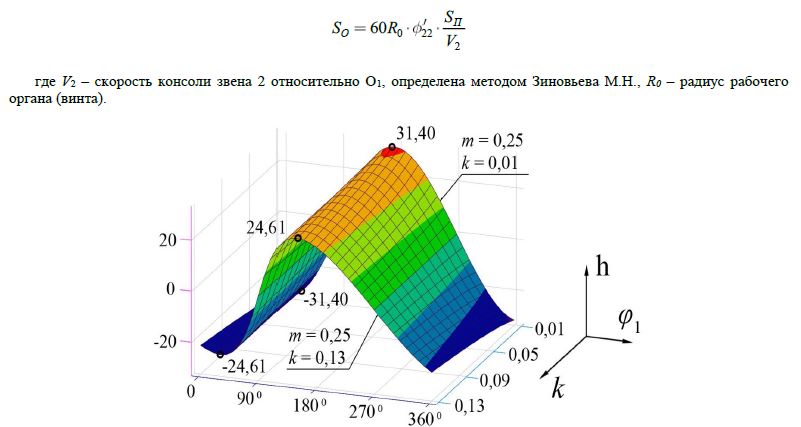
Рис. 6– Поверхность критерия оптимальности h= f(k,m,φ₁)

В пространстве относительных параметров k и m и угловой координаты кривошипаφ₁ при α=90° установлены значения k= 0,01 и m=0,25, при которых критерий h=f(k,m,φ₁) (рис. 6) принимает максимальные значения.

Отметим, что при выбранных значениях k и mуглы перекрытияθ₂ и дав­ленияνпринадлежат рекомендованным интервалам [4], тем самым обеспечи­вается благоприятное снижение динамических нагрузок на палец кривошипа А, повышается качество передачи сил в пространственной винтовой кинематической паре С (рис. 1,2).

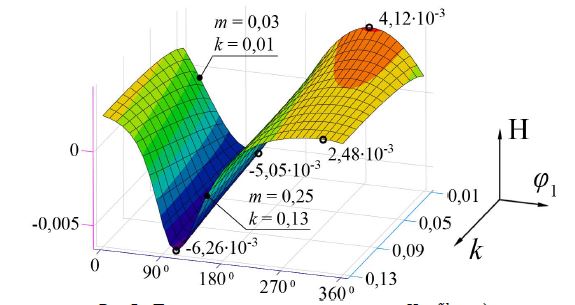
Рис. 7 – Поверхность критерия оптимальности Н = f(k,m,φ₁)

Установлено, что максимальные значения второго критерия Н = f(k,m,φ₁) для переносного движения звена 2, равное Н=(4,12∙10^–3;–5.05∙10^–3) (рис. 7), реализуется в механизмах с углами θ₂=ν£45⁰ [4] и длинами, удовлетворяю­щими относительным параметрам k=0,01 и m=0,03 .

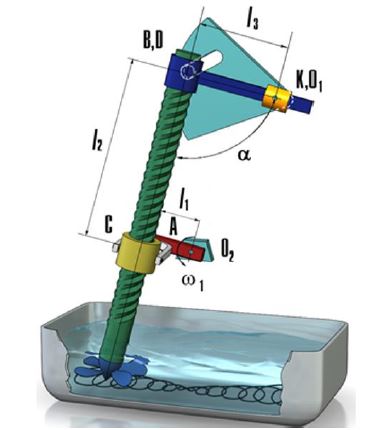
Таким образом, с целью реализации у критериев оптимальности как в переносном, так и относительном движениях максимальных значений, в механизме следует предусмотреть устройство, позволяющее автоматически, в течении рабочего цикла, дискретно изменять значение настроечного угла α, что в свою очередь, позволит провести переход размера О₁В с m=0,03 на m=0,25 (рис. 8)

Рис. 8 – Перемешивающее устройство

В работе установлено влияние расстояния между опорами стойки l₀ на параметры и при отобранных значениях kи m. Отметим, что увеличение значения l₀ не оказывает существенного влияния на критерий h оптимальности движения рабочего органа.

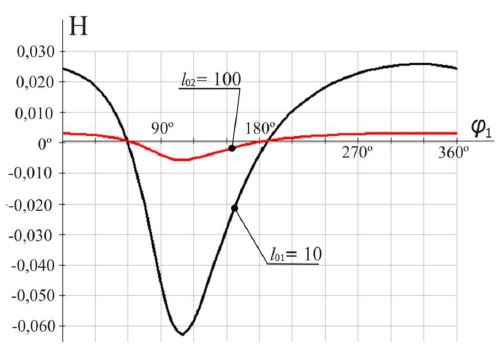
Увеличение размеров звеньев механизма при фиксированных параметрах k и m, обусловленное соответствующим изменением размера l₀, вне зависимости от соотношений углов перекрытия и давления (θ₂ = ν, θ₂ >νи θ₂<ν), приводит к уменьшению амплитуд критерия Н оптимальности движения рабочего органа вокруг О₁ (рис. 9).

Рис. 9 –Графики параметра движения Н = f(k,m,φ₁)

Таким образом предложена методика определения рациональных геометрических параметров механизма [8], [10] для достижения наилучших эксплуатационных характеристик механизма при прочих равных условиях.

Конфликт интересов Не указан.

Conflict of Interest None declared.

Список литературы / References

1. Дытнерский Ю.И. Процессы и аппараты химической технологии / Ю.И. Дытнерский. – М.: Химия, 2002. – Т. 1 – 2. – 400 с.
2. Иванец В. Н. Аппараты с перемешивающими устройствами: Учеб. пособие / В. Н. Иванец, В. Н. Зайцев. – Кемерово: Кемеров. технол. Ин–т пищевой пром–сти. 1993. – 135 с.
3. Gileta V.P. Parametric analysis of device for the mixng with the equal angles overlap and pressure / V.P. Gileta, N.. Choosovitin // IFOST – 2008. The 3^rd international strategic technologies. Novosibirsk, Russia: Proc. – NGTU, 2008. – Р. 414 – 416.
4. Гилета В.П. Параметрический синтез пространственного дезаксиального перемешивающего устройства /В.П. Гилета, Н.А. Чусовитин // Матер. IV Международной конференции «Проблемы механики современных машин». - Улан-Удэ: Изд. ВСГТУ, 2009. – Т. 2. – С. 22-28.
5. Гилета В. П. К вопросу кинематического исследования устрой­ства для перемешивания, с равными углами перекрытия q₂ и давления ν / В. П. Гилета, Н. А. Чусовитин // Межвуз. сб.// под ред. Н. В. Пустового. – Новосибирск. Изд. НГТУ, 2008г. – С. 128 –134.
6. Зурабишвили Л. А. Анализ и синтез четырех- и пятизвенных пространственных механизмов / Л. А. Зурабишвили. – Тбилиси: 1982. – 73 с.
7. Гилета В. П. Синтез пространственного кулисного дезаксиального механизма по углу перекрытия θ₂ / В. П. Гилета, А. И. Смелягин, Н. А. Чусовитин // Сборник докладов Междунар. конф. по теории мех–ов и механике машин. – Краснодар: Кубан. гос. технол. ун–т, 2006. – С. 50 –51.
8. Карелин В.С. Проектирование рычажных и зубчато-рычажных механизмов. Справочник / В.С. Карелин. – М.: Машиностроение, 1986. – 184 с.
9. Сумский С. Н. Расчет кинематических и динамических характеристик плоских рычажных механизмов: Справочник / С. Н. Сумский. – М.: Машиностроение, 1980. – 312 с.
10. Канунников И. А. Теория механизмов и машин / И.А. Канунников. – Красноярск: 2007. – 226 с.

Список литературы на английском языке / References in English

1. Dytnersky Yu.I. Processy i apparaty khimicheskojj tekhnologii [Processes and apparatuses of chemical technology] / Yu.I. Dytnersky. – M.: Khimiya, 2002. – Vol. 1-2. – 400 p. [in Russian]
2. Ivanets V. N. Apparaty s peremeshivajushhimi ustrojjstvami: Ucheb. posobie [Apparatuses with mixing devices: Textbook] / V. N. Ivanets, V. N. Zaitsev. – Kemerovo: Kemero Technological Institute of Food Industry. 1993. – 135 p. [in Russian]­
3. Gileta V.P. Parametric analysis of device for the mixng with the equal angles overlap and pressure / V.P. Gileta,N.. Choosovitin // IFOST – 2008. The 3^rd international strategic technologies. Novosibirsk, Russia: Proc. – NGTU, 2008. – p. 414 – 416 [in Russian]
4. Gileta V.P.Parametricheskijj sintez prostranstvennogo dezaksial'nogo peremeshivajushhego ustrojjstva [Parametric synthesis of a spatial deaxial mixing device] / V.P. Gileta, N.A. Chusovitin // Mater. IV Mezhdunarodnojj konferencii «Problemy mekhaniki sovremennykh mashin [Proceedings of the IV International Conference "Problems of mechanics of modern machines"]. - Ulan-Ude: Publishing House of VSSTU, 2009. – Vol. 2. – pp. 22-28 [in Russian]
5. Gileta V. P. K voprosu kinematicheskogo issledovanija ustrojjstva dlja peremeshivanija, s ravnymi uglami perekrytija 2 i davlenija ν [On the issue of kinematic investigation of the mixing device, with equal overlap angles 2 and pressure v] / P. Gileta, N. A. Chusovitin // Interacademic collection of studies // edited by N. V. Empty. – Novosibirsk. NSTU Publishing House, 2008 – pp. 128 -134 [in Russian]­
6. Zurabishvili L. A. Analiz i sintez chetyrekh- i pjatizvennykh prostranstvennykh mekhanizmov [Analysis and synthesis of four- and five-link ­spatial mechanisms] / L. A. Zurabishvili. – Tbilisi: 1982. – 73 p. [in Russian]
7. Gileta V. P. Sintez prostranstvennogo kulisnogo dezaksial'nogo mekhanizma po uglu perekrytija θInsert a tag (Alt+2)2 [Synthesis of a spatial rocker deaxial mechanism by the overlap angle θ ₂] / V. P. Gileta, A. I. Smelyagin, N. A. Chusovitin // Sbornik dokladov Mezhdunar. konf. po teorii mekh–ov i mekhanike mashin [Collection of reports of the International Conference on the theory of mechanisms and mechanics of machines]. – Krasnodar: Kuban. state. technol. un–t, 2006. – pp. 50-51 [in Russian]
8. Karelin V.S.Proektirovanie rychazhnykh i zubchato-rychazhnykh mekhanizmov. Spravochnik [Design of lever and gear-lever mechanisms. A Handbook] / V.S. Karelin. – M.: Mashinostroenie, 1986. – 184 p. [in Russian]
9. Sumy S. N.Raschet kinematicheskikh i dinamicheskikh kharakteristik ploskikh rychazhnykh mekhanizmov: Spravochnik [Calculation of kinematic and dynamic characteristics of flat lever mechanisms: A handbook] / S. N. Sumsky. – M.: Mashinostroenie, 1980. – 312 p. [in Russian]
10. Kanunnikov I. A. Teorija mekhanizmov i mashin [Theory of mechanisms and machines] / I.A. Kanunnikov. – Krasnoyarsk: 2007. – 226 p. [in Russian]