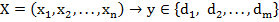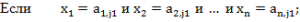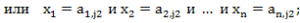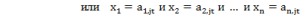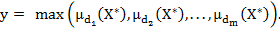ВЛИЯНИЕ ОБУЧАЮЩИХ ВЫБОРОК НА ПРОЦЕСС ОБУЧЕНИЯ АДАПТИВНЫХ НЕЙРО-НЕЧЕТКИХ СЕТЕЙ ДЛЯ РЕШЕНИЯ ЗАДАЧИ КЛАССИФИКАЦИЙ ДЕТАЛЕЙ

Нгуен Данг Минь

Аспирант, Иркутский государственный технический университет

ВЛИЯНИЕ ОБУЧАЮЩИХ ВЫБОРОК НА ПРОЦЕСС ОБУЧЕНИЯ АДАПТИВНЫХ НЕЙРО-НЕЧЕТКИХ СЕТЕЙ  ДЛЯ РЕШЕНИЯ ЗАДАЧИ КЛАССИФИКАЦИЙ ДЕТАЛЕЙ

Аннотация

В работе рассматривается задача классификации с помощью системы нечеткого вывода, описываются возможности ANFIS для решения задачи, и обсуждается влияние экспериментальных данных на качество получаемых результатов. Приводятся результаты применения ANFIS для создания системы классификации втулок, анализируется зависимость точности работы системы от количеств обучающих выборок.

Ключевые слова: нейро-нечеткая сеть, обучающая выборка, классификация деталей, система нечеткого вывода.

Nguyen Dang Minh

Postgraduate student, Irkutsk State Technical University

THE EFFECTS OF TRAINING DATA IN THE LEARNING PROCESS OF ADAPTIVE NEURAL-FUZZY NETWORKS FOR SOLVING THE PROBLEM OF CLASSIFICATION OF DETAILS

Abstract

This work consider the problem of fuzzy inference system for classification, describes possible solutions to the problem of ANFIS and the impact of experimental data on the quality of results. The application of ANFIS to create a classification system of plugs, depending on system accuracy is analyzed on the amounts of training data.

Key word: neural-fuzzy network, training data, classification of details, fuzzy inference system.

Введение

Детали, изготавливаемые на машиностроительных предприятиях, обрабатываются с использованием различных технологических процессов. Успешное решение задач унификации и нормализации технологических процессов в большой степени зависит от решения вопросов классификации объектов производства. Для решения задачи классификации деталей можно использовать различные информационные технологии, в том числе  адаптивные нейро-нечеткие сети, на основе которых генерируются системы нечеткого вывода [2, 3].

Адаптивные нейро-нечеткие сети или гибридные сети по замыслу их разработчиков призваны объединить в себе достоинства нейронных сетей и систем нечеткого вывода. С одной стороны, они позволяют разрабатывать и представлять модели систем в форме правил нечетких продукций, которые обладают наглядностью и простотой содержательной интерпретации. С другой стороны, для построения правил нечетких продукций используются методы нейронных сетей, что является более удобным и менее трудоемким процессом для системных аналитиков [4].

Вся информация, используемая сетью для построения системы нечеткого вывода,   содержится в множестве обучающих выборок. Поэтому качество обучения сети напрямую зависит от количества примеров, а также от того, насколько полно эти примеры описывают данную задачу.

В работе рассматривается возможность использования  системы нечеткого вывода для решения задачи классификации, формирование обучающих выборок для генерации системы классификации втулок с помощью ANFIS и анализируется точность системы.

Нечеткий логический вывод для задач классификации.

Классификация деталей дает возможность повысить технологичность конструкций деталей; решить вопросы выбора оптимального варианта производственной структуры участка, цеха, завода.

Нечеткая логика - обобщение традиционной Аристотелевой логики на случай, когда истинность рассматривается как лингвистическая переменная, принимающая значения «очень истинно», «более или менее истинно», «не очень ложно» и т.н. Эти лингвистические значения представляются «нечеткими множествами» [4].

Задача классификации состоит в отнесении объекта, заданного вектором информативных признаков 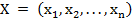, к одному из наперед описанных классов .

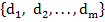Классификация соответствует отображению вида:

.

Для классификации необходима нечеткая база знаний вида:

 

 

 

  с некоторой степенью уверенности.

где 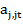 - нечеткий терм, которым оценивается переменная  x_i в правиле с номером  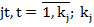 - количество правил, описывающих класс d_j.

Степени принадлежности объекта 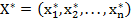 классам  рассчитывают по формул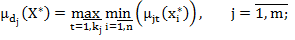е: где 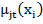 -функция принадлежности входа  x_i нечеткому терму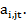 

В качестве решения выбирают класс с максимальной степенью принадлежности [4]:

 

Гибридная сеть как адаптивная система нейро-нечеткого вывода (ANFIS).

Гибридная сеть представляет собой многослойную нейронную сеть специальной структуры без обратных связей, в которой используются обычные (не нечеткие) сигналы, веса и функции активации.

Основная идея, положенная в основу модели гибридных сетей, заключается в том, чтобы использовать существующую выборку данных для определения параметров функций принадлежности, которые лучше всего соответствуют некоторой системе нечеткого вывода. При этом для нахождения параметров функций принадлежности используются известные процедуры обучения нейронных сетей.

С одной стороны, гибридная сеть ANFIS представляет собой нейронную сеть с единственным выходом и несколькими входами, которые представляют собой нечеткие лингвистические переменные. При этом термы входных лингвистических переменных описываются стандартными функциями принадлежности, а термы выходной переменной представляются линейной или константной функцией принадлежности.

С другой стороны, гибридная сеть ANFIS представляет собой систему нечеткого вывода FIS (fuzzy inference system) типа Сугено [4].

Решение задачи классификаций деталей с использованием ANFIS.

В вычислительную среду MATLAB интегрированы десятки пакетов прикладных инженерных и математических программ, одним из них является Fuzzy Logic Toolbox, который поддерживает все фазы разработки нечетких систем, включая синтез, исследование, проектирование, моделирование и внедрение в режиме реального времени [4]. Функции пакета реализуют большинство современных нечетких технологий, включая нечеткий логический вывод, нечеткую кластеризацию и адаптивную нейро-нечеткую настройку (ANFIS).

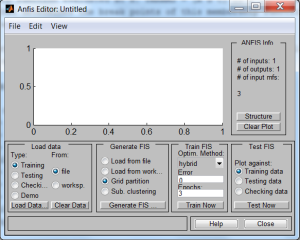
Рис.1 Окно редактора гибридных систем.

 

Редактор нейро-нечеткой сети (ANFIS Editor) позволяет автоматически синтезировать из экспериментальных данных нейро-нечеткие сети и настраивать их. Графический интерфейс гибридных нейронных систем вызывается из командного окна функцией аnfisedit. Исполнение функции приводит к появлению окна редактора гибридных систем, вид которого приведен на рис.1.

С помощью редактора осуществляется создание или загрузка структуры гибридной сети, просмотр структуры, настройка ее параметров, проверка качества функционировании такой системы. Создание структуры, настройка параметров и проверка осуществляются по выборкам (наборам данных) - обучающей (Training data), проверочной (Checking data) и тестирующей (Testing data), которые предварительно должны быть представлены в виде текстовых файлов (с расширением .dat и разделителями табуляциями), первые колонки которых соответствуют входным переменным, а последняя - единственной выходной переменной. Вид обучающей выборки представлен в табл.1.

Обучающая выборка будет использоваться в процессе настройки системы нечеткого вывода для классификации.

Данные записаны в файл data_learn.dat.

В режиме Load data (загрузить данные) выбираем Training и file, нажав кнопку Load Data ... ,загрузим файл data_learn.dat.

Затем в режиме Generate FIS (создание нечеткой системы вывода) выбираем Grid partition, нажимаем кнопку Generate FIS ..., появится  окно задания функции принадлежности. Для каждого входного параметра выбираем pimf - пи-подобную функцию принадлежности, а в качестве параметров функций задаем [6 6], чтобы создать по шесть термов для каждой входной переменной. Функция принадлежности выходной величины назначается как constant.

Рис.2 Результат обучения сети

 

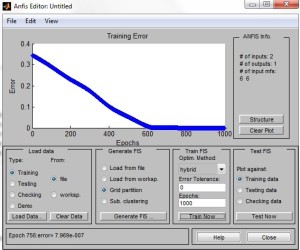
Далее зададим  режим обучения (Train FIS). Не будем менять задаваемые по умолчанию метод настройки параметров (hybrid - гибридный) и уровень ошибки (0), но количество циклов обучения зададим достаточно большим. Получившийся результат в виде графика ошибки сети в зависимости от числа проведенных циклов обучения  представлен на рис.2.

Влияние обучающих выборок на процесс обучения адаптивных нейро-нечетких сетей (НС).

При подготовке решения задачи на НС не всегда удается точно определить, сколько и каких входных данные нужно подавать на ее вход при обучении. В случае недостатка данных сеть не сможет обучиться решению задачи. Проблема усугубляется тем, что в большинстве плохо формализуемых областей человеческой деятельности эксперт часто не может точно сказать, какие именно данные являются важными. Поэтому обычно на вход сети подается избыточный набор данных. Для уменьшения времени обучения и повышения качества работы НС требуется определить, какие данные необходимы для решения конкретной задачи. Кроме того, в ходе решения этой задачи определяются значимости входных сигналов, что во многих предметных областях представляет самостоятельную ценность [1].

При отборе данных для НС необходимо учитывать следующие факты:

• при решении реальных задач с помощью НС довольно часто трудно установить связь выходного показателя с имеющимися данными, поэтому проводят сбор как можно большего числа данных;
• наличие корреляции между данными не позволяет произвести их ранжирование и, следовательно, невозможно использовать простой алгоритм отбраковки по степени важности.
• для того чтобы снизить действие фактора «очень большой размерности», часто просто удаляют некоторое число переменных; при этом возможно удаление таких, которые несут существенную информацию.

Чтобы гарантированно получить только полезные (информативные) данные, необходимо выполнить перебор большого количества наборов данных и архитектур НС. Однако практически это реализовать трудно даже при наличии мощных и эффективных нейроимитаторов [1, 5].

Экспериментальные результаты обучения ANFIS

В данной работе исследуется классификация втулок, которые имеют максимальные диаметры и высоты меньше 30 миллиметров, класс детали определен в соответствии с положениями, приведенными в [2, 3]: детали, характеризующиеся определенном соотношением высоты и максимального диаметра, попадут в определенный класс по технологии их обработки. Поэтому можно предположить наличие 5 классов для определенного соотношения высоты и диаметра, то есть 5 значений выходной величины в системе нечеткого вывода. Случайным образом были сгенерированы пять множеств обучающих примеров с разными размерами. В таблице 2 показан характер данных и ошибка обучения ANFIS  при использовании этих данных.

Таблица 2.
Количество обучающих примеров	Количество экземпляров каждого класса в каждом множестве обучающих примеров					Ошибка обучения ANFIS
	Класс 1	Класс 2	Класс 3	Класс 4	Класс 5
30	5	1	3	5	16	0.00003837
50	7	3	6	7	27	0.00000539
100	11	12	11	15	51	0.00000227
150	15	17	16	25	77	0.00000150
200	20	26	23	32	99	0.00000080

 

 

 

 

 

Из таблицы 2 видно, что при использовании описанной структуры нейро-нечеткой сети при обучении на разных множествах данных получены разные величины ошибок обучения системы нечеткого вывода. Чем больше число примеров, тем лучше полученный результат, значит, тем точнее система нечеткого вывода для классификации втулок.

Был реализован проверочный режим, фактически классифицирующий 34 реальные втулки на основе системы нечеткого вывода, сгенерированной ANFIS. Результаты приведены в табл. 3; они соответствуют фактическому распределению втулок по классам технологии. Из таблицы видно, что при классификации втулки № 16 наблюдается ошибка из-за неточности в процессе обучения ANFIS. Однако эта ошибка незначительная, то есть можно считать, что эта втулка попадает в класс 1.

Заключение

На основе проделанных экспериментов можно сделать вывод, что использование ANFIS для решения задачи классификации деталей является весьма перспективным. Недостатком является то, что качество результатов зависит от качества экспериментальных данных или обучающих выборок. Поэтому отбор обучающих выборок является важным процессом при использовании ANFIS.