ВЛИЯНИЕ ПРОДОЛЬНОЙ ЖЕСТКОСТИ ПУТИ НА ВОЗМОЖНОСТЬ ПРОСКАЛЬЗЫВАНИЯ КОЛЕСНЫХ ПАР ЛОКОМОТИВА ПРИ ДВИЖЕНИИ В РЕЖИМЕ ТЯГИ
Новосельцев В. П.1,Новосельцев П.В.2, Гордеева А.А.3
1Кандидат технических наук, доцент, Улан-Удэнский институт железнодорожного транспорта; 2кандидат технических наук; 2Улан-Удэнский институт железнодорожного транспорта; 3аспирант, Иркутский государственный университет путей сообщения
ВЛИЯНИЕ ПРОДОЛЬНОЙ ЖЕСТКОСТИ ПУТИ НА ВОЗМОЖНОСТЬ ПРОСКАЛЬЗЫВАНИЯ КОЛЕСНЫХ ПАР ЛОКОМОТИВА ПРИ ДВИЖЕНИИ В РЕЖИМЕ ТЯГИ
Аннотация
Рассматривается влияние продольной жесткости рельсового пути, его податливости под действием силы тяги на процесс взаимодействия колесной пары и рельса.
Ключевые слова: продольная динамика рельсового пути, приведенная жесткость.
Novoseltsev V.P1., Novoseltsev P.V.2, Gordeeva A.A.3
1PhD of Technical Sciences, assistant professor, Ulan-Ude institute of railway transport; 2PhD of Technical Sciences, Ulan-Ude institute of railway transport; 3Postgraduate stuent, Irkutsk state university of means of communication
THE INFLUENCE OF LONGITUDINAL FLEXIBILITY OF A RAILWAY LINE UPON THE POSSIBILITY OF THE LOCOMOTIVE SET OF WHEELS SLIDING WHEN MOVING IN THE MODE OF TRACTION
Abstract
The purpose of this paper is to evaluate the influence of longitudinal flexibility and compliance of a railway line under the propulsive force action on the process of interaction between the set of wheels and the rail.
Keywords: longitudinal dynamics of a railway line, the resulted flexibility.
Рассмотрим частный случай – колесная пара въезжает на конец рельса А-В длиной ℓ; на колесную пару действует движущий момент Мдв (Рис. 1).
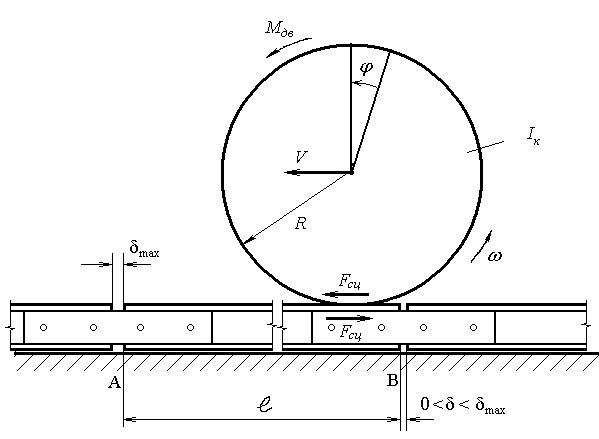
Рис. 1 - Схема взаимодействия рельсового пути и колесной пары
Стык А рельса полностью раскрыт, поэтому поступательное смещение рельса исключено. На рельс действуют силы сопротивления; предположим, что они существенно ослаблены и ими можно пренебречь. Под действием Fсц – силы сцепления колеса с рельсом происходит упругая деформация рельса; жесткость рельсового пути при этом:
 , (1)
, (1)
где:  – модуль упругости рельсового пути;
– модуль упругости рельсового пути;
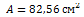 – площадь поперечного сечения рельса;
– площадь поперечного сечения рельса;
ℓ = 25 м – длина рельса.
Получим:
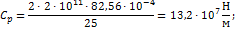
Движущий момент, на основании исследования [1] можно считать изменяющимся по закону:
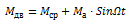 , (2)
, (2)
где 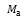 - амплитуда колебания движущего момента. Для грузовых локомотивов можно принять [1]:
- амплитуда колебания движущего момента. Для грузовых локомотивов можно принять [1]:
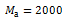 Нм.
Нм.
Частоту изменения движущего момента на основании того же источника можно принять:
 = 32 с-1
= 32 с-1
Сила сцепления колеса с рельсом:
 ; (3)
; (3)
Реакция рельса, как упругой пружины:
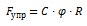 ; (4)
; (4)
Дифференциальное уравнение вращательного движения колесной пары в режиме малых колебаний. Представим угол поворота колесной пары состоящим из двух частей:
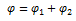 ; (5)
; (5)
где 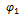 - основное угловое перемещение в режиме плоского движения колесной пары;
- основное угловое перемещение в режиме плоского движения колесной пары;
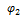 - дополнительное малое угловое перемещение колесной пары, вызванное гармонической составляющей движущего момента
- дополнительное малое угловое перемещение колесной пары, вызванное гармонической составляющей движущего момента 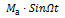 .
.
Дифференциальное уравнение малых угловых перемещений колесной пары:
 , (6)
, (6)
или
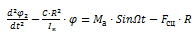 , (7)
, (7)
где
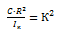 ; (8)
; (8)
– квадрат собственной частоты колебаний.
Для нашего случая:
 =
= ;
;
Решение дифференциального уравнения (7) имеет вид:
 =
= ; (9)
; (9)
Для конкретного примера: 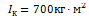 ;
; 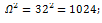
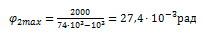 ;
;
Максимальное линейное смещение точки обода колеса:
 ;
;
Угловая скорость малых колебаний:
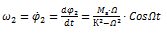 ; (10)
; (10)
Для нашего случая:
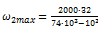 =0,88 с-1;
=0,88 с-1;
Смещение точки касания рельса под действием силы сцепления колеса с рельсами (для передней колесной пары):
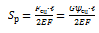 ; (11)
; (11)
Для нашего случая:
 ;
;
Разность:
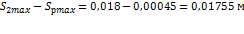 ;
;
представляет собой линейное скольжение колеса по рельсу.
Линейная скорость проскальзывания:
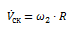 ; (12)
; (12)
Относительная скорость проскальзывания:
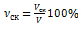 ; (13)
; (13)
Рассмотренный выше случай является предельно неблагоприятным для возникновения проскальзывания. В практике наиболее вероятен случай, когда продольная жесткость рельсового пути значительно выше, чем в нашем случае. В общем случае продольную жесткость рельсового пути, как отношение некоей осевой силы Fрасч , приложенной к рельсу, и вызывающей упругое смещение Δ, к величине этого смещения (Рис. 2):
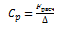 ; (14)
; (14)

Рис. 2 - Схема упругой деформации рельса
По сути, продольная жесткость рельсового пути, это жесткость самого рельса длиной ℓрасч. Здесь ℓрасч- расчетная длина, зависящая от состояния рельсового пути и определяемая опытным путем. Нами выполнены эксперименты [2], которые позволяют утверждать, что расчетная длина ℓрасч при силе Fрасч = 100 кН колеблется в широких пределах от 8 до 40 метров в зависимости от состояния рельсового пути, погодных условий, длины рельсов, способов крепления и т.д.
Список литературы
Зарифьян А. А. и др. Динамические процессы в асинхронном тяговом приводе магистральных электровозов. М. 2006, С. 351.
Новосельцев В. П., Гордеева А. А. Исследования продольной жесткости рельсового пути. (Сборник трудов сотрудников кафедры ВПО УУИЖТ. Улан-Удэ, 2012.
