ПРОГРАММНАЯ РЕАЛИЗАЦИЯ НАХОЖДЕНИЯ МИНИМАЛЬНО ЖЕСТКИХ ГРАФОВ

Степович-Цветкова Г.С.¹, Цветков А.А.²

¹Кандидат экономических наук, Ивановский государственный университет; ²аспирант, Шуйский филиал Ивановского государственного университета

ПРОГРАММНАЯ РЕАЛИЗАЦИЯ НАХОЖДЕНИЯ МИНИМАЛЬНО ЖЕСТКИХ ГРАФОВ

Аннотация

Описан алгоритм и особенности его программной реализации для нахождения минимально жестких графов с заданным количеством вершин.

Ключевые слова: алгоритм, программа, минимально жесткие графы, ламановы графы.

Stepovitch-Tsvetkova G.S.¹, Tsvetkov A.A.²

¹PhD in economic, Ivanovo State University; ²Postgraduate student, Shuya, Ivanovo State University branch

SOFTWARE IMPLEMENTATION OF FINDING HARD MINIMAL GRAPHS

Abstract

It is described the algorithm of finding hard minimal graphs with a given number of vertices and the features of its software implementation.

Keywords: algorithm, program, hard minimal graphs, Lamanov graphs.

Достаточно популярной структурой данных в программировании является граф, который используется во многих алгоритмах. Динамично развивающейся в данное время является область изучения шарнирных механизмов, где также используется понятие графа, причем одной из задач является нахождение так называемых минимально жестких, или ламановых, графов с заданным количеством вершин, то есть таких, при удалении любого ребра у которых они становились бы изгибаемыми.

При этом жесткость – это свойство тела,  заключающееся в том, что любое его движение в пространстве является тривиальным, то есть тело движется исключительно как «единое целое» и расстояние между любыми двумя его точками не изменяется.

Целью работы является построение и программная реализация алгоритма нахождения всех минимально жестких графов с заданным количеством вершин. То есть по заданному значению n – количеству вершин необходимо найти всевозможные минимально жесткие графы, порожденные этими вершинами (рис. 1).

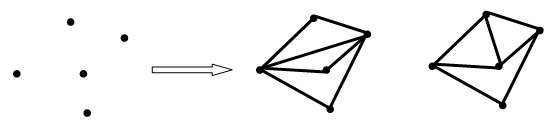
Рис. 1 – Постановка задачи

Построение ламановых графов может быть основано на теореме Ламана, согласно которой граф является минимально жестким тогда и только тогда, когда выполнены два условия: 1) m = 2n–3 (m – количество ребер); 2) всякий набор из k вершин порождает не более чем 2k–3 ребра.

Для описания алгоритма введем ряд понятий. Совокупность степеней всех вершин графа, упорядоченная по убыванию, назовем степенной характеристикой этого графа. Расширенной степенной характеристикой графа будем называть множество из n совокупностей чисел, где n – количество вершин. Каждая такая i-я совокупность характеризует некоторую j-ю вершину графа и состоит из степеней вершин, соединенных с j-ой вершиной ребром (i,j=1,...,n). Элементы совокупности упорядочены по убыванию, а сами совокупности внутри множества упорядочены по убыванию степеней вершин.

Итак, представляется следующий алгоритм нахождения матриц смежности для минимально жестких графов. По заданному n – количеству вершин строим всевозможные степенные характеристики с условием, что степень каждой вершины больше единицы, но меньше n, а также сумма всех степенных характеристик равна удвоенному количеству ребер. Количество ребер m находим из первого условия теоремы Ламана. Затем для каждой степенной характеристики строим всевозможные матрицы смежности. Каждую матрицу смежности проверяем на второе условие теоремы Ламана, и таким образом, получаем матрицы, соответствующие минимально жестким графам. После чего исключаем одинаковые графы с точностью до переименования вершин, во-первых, сравнивая расширенные степенные характеристики, во-вторых, проверяя матрицы смежности на изоморфность в случае, если  расширенные степенные характеристики получаются одинаковыми.

Для реализации данного алгоритма была написана компьютерная программа средствами Microsoft Visual Studio 2008 на языке программирования C#.

Для построения всевозможных степенных характеристик по заданному количеству вершин n реализована рекурсивная функция, в которую в качестве параметров передаются: количество вершин графа; массив для записи степеней вершин графа; номер текущей позиции, из которой ведется заполнение следующей; заполняемое значение; сумма степеней вершин. Если сумма степеней вершин положительна и не весь массив степенных характеристик заполнен, то есть может быть заполнена ячейка для степени следующей вершины, тогда следующая за текущей ячейка заполняется переданным значением, и сумма степеней уменьшается на это значение. Если дальнейшее заполнение оказывается невозможным, происходит возврат на шаг назад. Функция рекурсивно вызывается для каждого возможного заполняемого значения (1 < zn < n-1), начиная с большего, чтобы степенная характеристика была упорядочена по убыванию. Данная функция позволяет получить все степенные характеристика для заданного числа n.

Функция отыскания матриц смежности требует в качестве входных данных степенную характеристику для заданного количества вершин. Строка матрицы рекурсивно заполняется пока позволяет степень вершины единицами. Если на некотором шаге матрица не выстраивается, происходит возврат к последней поставленной единице, она заменяется на ноль, и происходит перестановка единицы на следующую позицию. Результат выводится при успешном заполнении матрицы до конца.

Функция проверки графа, заданного матрицей смежности, на второе условие теоремы Ламана, перебирает все наборы из k вершин (k=4,…,n-1), считает количество порожденных ими ребер и сопоставляет с 2k–3.

Для того чтобы исключить одинаковые графы с точностью до переименования вершин, достаточно проверить матрицы смежности на изоморфность, но для оптимизации программы сначала сравниваются расширенные степенные характеристики, что позволяет сократить число производимых операций. Затем если  расширенные степенные характеристики получаются одинаковыми, происходит проверка матриц смежности на изоморфность, для этого находятся всевозможные перестановки строк и столбцов матриц.

Результатом работы программы является набор, включающий в себя все степенные характеристики и матрицы смежности для найденных ламановых графов с заданным количеством вершин.