ИССЛЕДОВАНИЕ ПОТЕНЦИАЛЬНЫХ ВОЗМОЖНОСТЕЙ РАЗРЕШЕНИЯ ЦЕЛЕЙ ПО АЗИМУТУ В СИСТЕМАХ ЛОКАЦИИ
Решетняк Р.А.1, Власова К.В.2, Пахотин В.А.3
1Магистрант; 2кондидат физико-математических наук; 3доцент физико-математических наук, Балтийский федеральный университет им. И. Канта
ИССЛЕДОВАНИЕ ПОТЕНЦИАЛЬНЫХ ВОЗМОЖНОСТЕЙ РАЗРЕШЕНИЯ ЦЕЛЕЙ ПО АЗИМУТУ В СИСТЕМАХ ЛОКАЦИИ
Аннотация
Представлен новый метод обработки информации в системах локации. Он основан на положениях теории оптимального приема. В качестве принятого сообщения используется зависимость напряжения на выходе локационного приемника от угла сканирования диаграммой направленности антенной системы. Приводятся теоретические положения и результаты предварительных модельных расчетов. Показана возможность увеличения азимутального разрешения двух целей без изменения пространственной базы сигнала.
Ключевые слова: метод обработки информации в системах локации, метод максимального правдоподобия, увеличение азимутального разрешения двух целей.
Reshetniak R.A.1, Vlasov K.V.2, Pakhotin V.A.3
1Master student; 2kondidat physical and mathematical science; 3associate professor of Physics and Mathematics science, Immanuel Kant Baltic federal university
RESEARCH POTENTIAL TARGETS FOR PERMISSION AZIMUTH LOCATION SYSTEMS
Abstract
The new method of information processing in location systems is presented. It is based on provisions of the theory of optimum reception. As the accepted message dependence of tension at the exit of the locational receiver from a corner of scanning is used by the directional pattern of antenna system. Theoretical provisions and results of preliminary model calculations are given. Possibility of increase in azimuthal permission of two purposes without change of spatial base of a signal is shown.
Keywords: information processing method in location systems, maximum likelihood method, increase in azimuthal permission of two purposes.
Введение
Разрешающая способность локатора по азимуту является одним из наиболее важных параметров. Даже небольшое увеличение разрешающей способности локатора позволяет увеличить достоверность и точность информации об окружающем пространстве. В частности это относится к разрешению двух и более целей по азимуту. В настоящее время задача разрешения целей по азимуту решается с помощью узких диаграмм направленности антенных устройств. Сканируя диаграммой направленности в определенном азимутальном секторе можно получить функциональную зависимость амплитуды сигнала от азимута. Эта зависимость будет содержать столько максимумов, сколько целей будет в азимутальном секторе.

Рис.1 - Схема работы локатора при приеме двух целей
Если диаграмма направленности направлена на первую цель, то реализуется максимум функции на выходе приемника с азимутом
на выходе приемника с азимутом 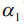 . Аналогично получается максимум функции
. Аналогично получается максимум функции 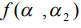 с азимутом
с азимутом 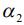 ,. Однако если цели по азимуту будут ближе, чем полуширина диаграммы направленности, то два отклика от двух близких по азимуту целей (две диаграммы направленности) будут сливаться вместе. В этом случае различить (разрешить) две цели оказывается невозможно. Для увеличения разрешающей способности локатора по азимуту ширину диаграммы направленности стараются сделать как можно меньше. Однако это можно сделать лишь за счет увеличения размера антенной системы при заданной длине волны
,. Однако если цели по азимуту будут ближе, чем полуширина диаграммы направленности, то два отклика от двух близких по азимуту целей (две диаграммы направленности) будут сливаться вместе. В этом случае различить (разрешить) две цели оказывается невозможно. Для увеличения разрешающей способности локатора по азимуту ширину диаграммы направленности стараются сделать как можно меньше. Однако это можно сделать лишь за счет увеличения размера антенной системы при заданной длине волны
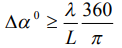 (1)
(1)
где λ – длина волны,
L – размер антенной системы
Следовательно, чем больше размер антенной системы, тем уже главный лепесток диаграммы направленности и выше разрешающая способность локатора. Однако для больших по размеру антенн требуются большие мощности для их сканирования по азимуту. В современных локаторах такая возможность увеличения разрешающей способности по азимуту практически исчерпана.
В настоящей работе предлагается новый метод увеличения разрешающей способности локатора по азимуту. Его основой являются положения теории оптимального приема [1,2]. Однако они применены не к временному сообщению, а к функциональной зависимости, которая получается на выходе локационного приемника при сканировании диаграммой направленности в азимутальном секторе.
Теоретические положения
Будем считать принятое сообщение суперпозицией подобных сигналов в азимутальном пространстве. Для ясности изложения ограничимся случаем суперпозиции двух сигналов. В этом случае принятое сообщение можно записать в виде
 , (2)
, (2)
где 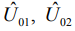 - комплексные амплитуды сигналов, представленных в азимутальном пространстве;
- комплексные амплитуды сигналов, представленных в азимутальном пространстве;
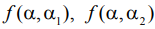 - азимутальные зависимости сигналов с направлений
- азимутальные зависимости сигналов с направлений 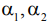 ;
;
 - аддитивный гаусовский шум со средним значением, равным нулю и дисперсией
- аддитивный гаусовский шум со средним значением, равным нулю и дисперсией 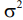 .
.

Интервал корреляции шумовой составляющей определяется пространственным фильтром Фурье 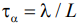 (
(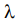 - длина волны,
- длина волны, - апертура антенной системы). Диаграмма направленности плоско – параболической антенной системы с прямоугольным раскрывом определяется выражением, которое можно получить с помощью углового преобразования Фурье /3 /
- апертура антенной системы). Диаграмма направленности плоско – параболической антенной системы с прямоугольным раскрывом определяется выражением, которое можно получить с помощью углового преобразования Фурье /3 /
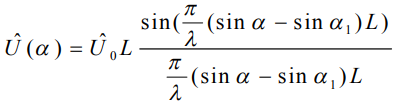 (3)
(3)
где  - апертура антенной системы.
- апертура антенной системы.
Ее вид показан на рис.2. Ширина диаграммы направленности 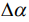 определяется размером зеркала
определяется размером зеркала  , точнее отношением длины волны к размеру зеркала. Если цели разнесены по азимуту достаточно далеко, тогда отмечаются два максимума с азимутами на первую и вторую цели. Если азимутальное различие не превышает полуширины диаграммы направленности, тогда два максимума сливаются в один и классическими методами их разделить невозможно.
, точнее отношением длины волны к размеру зеркала. Если цели разнесены по азимуту достаточно далеко, тогда отмечаются два максимума с азимутами на первую и вторую цели. Если азимутальное различие не превышает полуширины диаграммы направленности, тогда два максимума сливаются в один и классическими методами их разделить невозможно.
На основании выражения (2) запишем функционал правдоподобия [1,2]
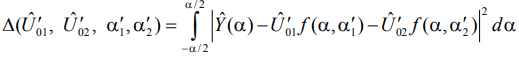 , (4)
, (4)
где 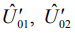 - оценочные (штрихованные) значения амплитуд составляющих сигнала;
- оценочные (штрихованные) значения амплитуд составляющих сигнала;
 - оценочные значения азимутов плоских волн.
- оценочные значения азимутов плоских волн.
Дифференцируя выражение (4) по оценочным амплитудам и приравнивая дифференциалы к нулю, получим систему уравнений правдоподобия. Они дают следующие решения
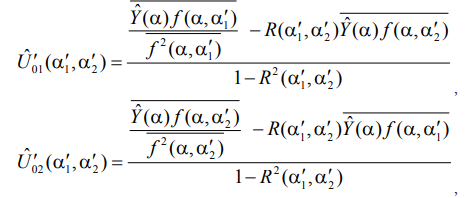 (5)
(5)
где
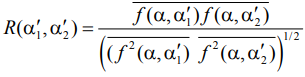 - коэффициент корреляции между сигналами в азимутальном пространстве; черта сверху означает интегрирование по азимуту
- коэффициент корреляции между сигналами в азимутальном пространстве; черта сверху означает интегрирование по азимуту 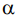 .
.
В этих выражениях значения оценочных азимутов 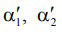 произвольные. Однако, если выражения для
произвольные. Однако, если выражения для 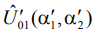 и
и 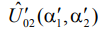 подставить в функционал правдоподобия (4), то исключается зависимость функционала от амплитуд сигнала. Остается зависимость только от оценочных азимутов. Возведем выражение (4) в квадрат и учтем уравнения правдоподобия, тогда выражение для функционала правдоподобия запишется в виде
подставить в функционал правдоподобия (4), то исключается зависимость функционала от амплитуд сигнала. Остается зависимость только от оценочных азимутов. Возведем выражение (4) в квадрат и учтем уравнения правдоподобия, тогда выражение для функционала правдоподобия запишется в виде
 , (6)
, (6)
где знак «*» обозначает комплексное сопряжение.
Полученное выражение определяет поверхность функционала правдоподобия в двумерном пространстве оценочных азимутов 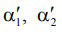 . Минимум этой поверхности определяет одновременно азимуты на первую и вторую цели, а с учетом (5) и амплитуды сигналов. Таким образом, задача оказывается решенной.
. Минимум этой поверхности определяет одновременно азимуты на первую и вторую цели, а с учетом (5) и амплитуды сигналов. Таким образом, задача оказывается решенной.
Результаты модельных расчетов
В соответствие с данной методикой была подготовлена программа для проведения модельных расчетов. Результаты расчетов представлены на следующих рисунках. На рисунке 3 коэффициент корреляции между азимутальными откликами близок к нулю.
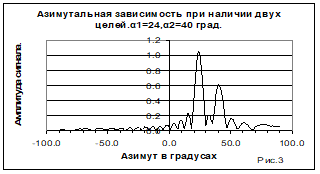

Две цели по азимуту разнесены на достаточное расстояние. По максимумам можно определить азимуты на две цели и их амплитуды. На рисунке 4 азимутального разнесения недостаточно для разрешения двух целей по азимуту. Различие азимутов на цели 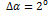 меньше, чем полуширина диаграммы направленности
меньше, чем полуширина диаграммы направленности 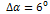 . Две диаграммы направленности сливаются, и их конфигурация в зависимости от разности фаз может существенно изменяться. При разности фаз, равной нулю, они усиливают друг друга. При разности фаз, равной 180 градусов, они подавляют друг друга.
. Две диаграммы направленности сливаются, и их конфигурация в зависимости от разности фаз может существенно изменяться. При разности фаз, равной нулю, они усиливают друг друга. При разности фаз, равной 180 градусов, они подавляют друг друга.
По новой методике решения находятся по максимуму поверхности обратного функционала правдоподобия 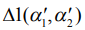 . Поверхность обратного нормированного функционала правдоподобия определяется выражением
. Поверхность обратного нормированного функционала правдоподобия определяется выражением
 (7)
(7)
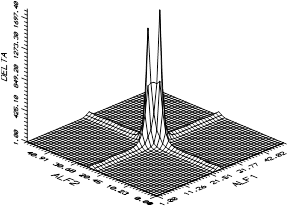
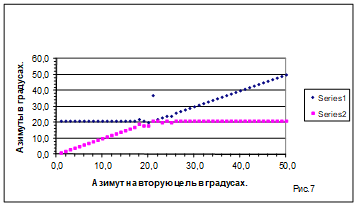
где черта сверху обозначает интегрирование по азимуту 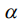 . На рисунке 5 показана поверхность функционала при большом разнесении целей по азимуту. Отмечается наличие двух максимумов функционала на плоскости азимутов. Один из них является зеркальным отображением первого. Однако зеркальный максимум не мешает найти два азимута на цели
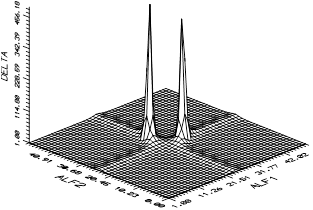
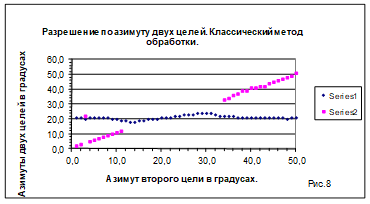
. На рисунке 5 показана поверхность функционала при большом разнесении целей по азимуту. Отмечается наличие двух максимумов функционала на плоскости азимутов. Один из них является зеркальным отображением первого. Однако зеркальный максимум не мешает найти два азимута на цели  . Во втором случае близких целей (рисунок 6) максимум функционала также позволяет получить оценки азимутов
. Во втором случае близких целей (рисунок 6) максимум функционала также позволяет получить оценки азимутов 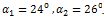
| Рис. 5 | Рис. 6 |
 |
 |
Один из них является зеркальным отображением первого. Однако зеркальный максимум не мешает найти два азимута на цели 
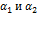 . Во втором случае близких целей (рисунок 6) максимум функционала также позволяет получить оценки азимутов
. Во втором случае близких целей (рисунок 6) максимум функционала также позволяет получить оценки азимутов 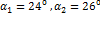
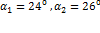
 |
 |
На рис.7 показаны азимуты на две цели, полученным методом максимального правдоподобия (МП). Азимут на первую цель постоянен и равен 21 градусу. Азимут на вторую цель меняется от 50 градусов до нуля градусов. Из рисунка ясно , что разрешение целей возможно в пределах углового различия азимутов 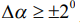 . При увеличении отношения сигнал/шум допустимое угловое различие азимутов
. При увеличении отношения сигнал/шум допустимое угловое различие азимутов 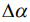 уменьшается.
уменьшается.
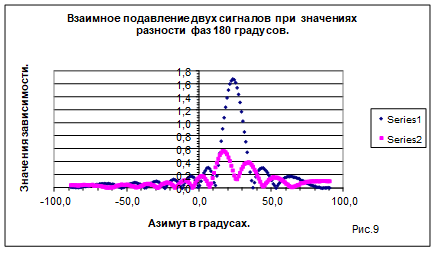
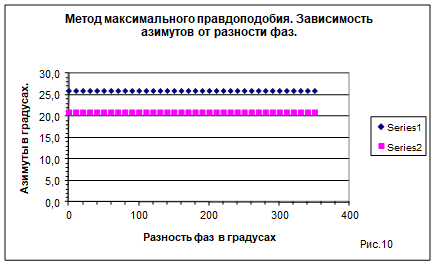
На рис. 8 показано аналогичное построение для классического способа обработки сигналов. Классический метод обработки позволяет разрешать азимуты на две цели в пределах 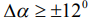 . Таким образом, метод МП позволяет увеличить разрешение целей по азимуту в 6 раз по сравнению с классическим методом обработки. В классическом методе обработки сигналов решение зависит от разности фаз между сигналами. Если разность фаз находится в пределах 180 градусов ,то диаграммы направленности от разных сигналов взаимно подавляют друг друга. Это показано на рис 9, где кривая (ряд 1) определяет суммарную диаграмму направленности при разности фаз ~ 70 градусов. Вторая кривая (ряд2) иллюстрирует изменение суммарной диаграммы направленности при разности фаз, равной 180 градусов. В результате оценки азимутов двух сигналов оказываются зависящими от разности фаз. Метод максимального правдоподобия полностью исключает погрешности оценки параметров двух сигналов, возникающие за счет изменения разности фаз между ними. На рис.10 показаны азимуты на цели (21 и 26 градусов) в зависимости от разности фаз между сигналами. Азимуты двух целей согласно рисунка не зависят от разности фаз.
. Таким образом, метод МП позволяет увеличить разрешение целей по азимуту в 6 раз по сравнению с классическим методом обработки. В классическом методе обработки сигналов решение зависит от разности фаз между сигналами. Если разность фаз находится в пределах 180 градусов ,то диаграммы направленности от разных сигналов взаимно подавляют друг друга. Это показано на рис 9, где кривая (ряд 1) определяет суммарную диаграмму направленности при разности фаз ~ 70 градусов. Вторая кривая (ряд2) иллюстрирует изменение суммарной диаграммы направленности при разности фаз, равной 180 градусов. В результате оценки азимутов двух сигналов оказываются зависящими от разности фаз. Метод максимального правдоподобия полностью исключает погрешности оценки параметров двух сигналов, возникающие за счет изменения разности фаз между ними. На рис.10 показаны азимуты на цели (21 и 26 градусов) в зависимости от разности фаз между сигналами. Азимуты двух целей согласно рисунка не зависят от разности фаз.
Заключение
В настоящей работе представлен новый метод обработки сигналов в системах локации. По результатам модельных расчетов можно сделать следующие выводы. Метод позволяет увеличить разрешение целей по азимуту по сравнению с Рэлеевским разрешением. Наряду с высоким разрешением целей по азимуту метод увеличивает точности оценок параметров сигнала в связи с интегральной обработкой данных. В классическом методе оценка азимута производится в точке - по максимуму азимутальной реализации. Динамический диапазон оценки двух сигналов ограничен уровнем шума и превосходит динамический диапазон классического метода обработки азимутальных реализаций.
Таким образом, согласно новому методу азимутальное разрешение целей зависит от отношения сигнал/шум, но не связано с размером антенной системы. Новый метод дает возможность улучшить разрешение целей по азимуту в несколько раз.
Список литературы
Перов А.И. Статистическая теория радиотехнических систем. Учебное пособие для вузов.- М.: Радиотехника, 2003, 400 с.
В.А.Пахотин, В.А.Бессонов, С.В. Молостова, К.В.Власова. Теоретические основы оптимальной обработки сигналов: Курс лекций для радиофизических специальностей .-Калининград:Из-во РГУ им И.Канта, 2008.-189 с.
А.Л. Драбкин, В.Л. Зузенко, А.Г.Кислов. Антенно-фидерные устройства. Изд.2-е.М., «Сов. радио», 1974.536 с.
Книхута Е.В. ,Пахотин В.А., Будник С.С., Ржанов А.А.Решение задачи оценки параметров сигнала в частотном пространстве // Изв.вузов России. Радиоэлектроника. 2005.Вып.2.С.
