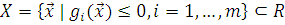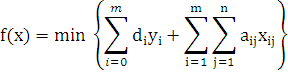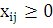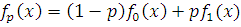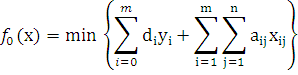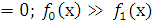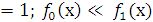РАЗРАБОТКА КРИТЕРИЕВ ВЫБОРА ОКОНЧАТЕЛЬНОГО РЕШЕНИЯ ПРИ ПОИСКЕ ИНСТРУМЕНТА В ЭКСПЕРТНОЙ СИСТЕМЕ ТЕХНОЛОГИЧЕСКОГО НАЗНАЧЕНИЯ

Филиппов А. Н.

Доцент, кандидат технических наук, Санкт-Петербургский национальный исследовательский университет информационных технологий, механики и оптики

РАЗРАБОТКА КРИТЕРИЕВ ВЫБОРА ОКОНЧАТЕЛЬНОГО РЕШЕНИЯ ПРИ ПОИСКЕ ИНСТРУМЕНТА В ЭКСПЕРТНОЙ СИСТЕМЕ ТЕХНОЛОГИЧЕСКОГО НАЗНАЧЕНИЯ

Аннотация

В статье описывается математическая модель оптимизации размещения инструментов по поверхностям для двух критериев, и реализация модели, применяя метод “ветвей и границ” и генетический алгоритм.

Ключевые слова: автоматизация, генетический алгоритм, метод ветвей и границ.

Filippov A. N.

Associate Professor, candidate of technical Sciences, Saint-Petersburg national   research University of information technologies, mechanics and wholesale

DEVELOPMENT  OF CRITERIA OF A CHOICE OF A FINAL SOLUTION WHEN SEARCHING FOR A TOOL IN THE EXPERT SYSTEM OF TECHNOLOGICAL PURPOSE

Abstract

The article describes the mathematical model of optimization of placement of instruments on surfaces for two criteria, and implementation of the model applying the method of branches and borders” and the genetic algorithm.

Keywords: automation, genetic algorithm, the method of branches and borders.  

Задачей оптимизации в математике называется задача о нахождении экстремума (минимума или максимума) вещественной функции в некоторой области. Как правило, рассматриваются области, принадлежащие R_n  и заданные набором равенств и неравенств.

Для того чтобы корректно поставить задачу оптимизации необходимо задать:

1. Допустимое множество 
2. Целевую функцию — отображение 
3. Критерий поиска (max или min).

Существующие в настоящее время методы поиска можно разбить на три большие группы: детерминированные, случайные, комбинаторные.

В случае с одним параметром задача оптимизации размещения [2] инструментов по поверхностям [3] выглядит так:

Минимизировать функцию:

 

при ограничениях:

 y_i = 0, если  x_ij для всех j=1...n

  y_i= 1, в остальных случаях

где:

a_ij– стоимость обработки j-й поверхности i-м инструментом

d_i – стойкость i-ого инструмента (фиксированная доплата)

n – количество инструментов

m – количество поверхностей

x_ij= 1 – для обработки  j-й поверхности выбран i-й инструмент

x_ij= 0 –инструмент не выбран

 y_i= 1 – i-й инструмент используется

 y_i= 0 – i-й инструмент не используется

Для того чтобы решить задачу оптимизации для двух критериев требуется минимизировать взвешенную сумму функций f₀(x) и f₁(x):

 

где:

 

 

p – параметр, лежащий в пределах от 0 до 1, учитывающий степень стоимости функции  f₀(x) по сравнению с f₁(x).

Например:

• При p  (f₀ много дороже, чем f₁)
• При p (f₀ много дешевле, чем f₁)

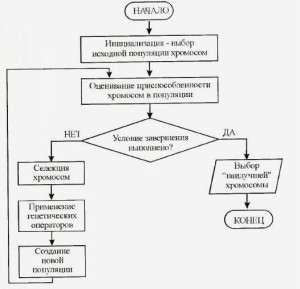
Рис. 1 Блок схема генетического алгоритма

На рис.1 представлена блок схема генетического алгоритма для решения задачи оптимизации с двумя критериями [1].

В результате проделанной работы разработана математическая модель, которая описывает алгоритм оптимизации размещения инструментов по поверхностям в случае с двумя параметрами, а также представлен модернизированный до двух критериев алгоритм оптимизации на основе методов: генетические алгоритмы, метод ветвей и границ.