ОПТИМИЗАЦИОННЫЙ МЕТОД ОПРЕДЕЛЕНИЯ ТЕМПЕРАТУРЫ ТРУДНОДОСТУПНОЙ ДЛЯ ИЗМЕРЕНИЯ

Телгожаева Ф.С.

Магистр, КазНУ имени аль-Фараби, Казахстан

ОПТИМИЗАЦИОННЫЙ МЕТОД ОПРЕДЕЛЕНИЯ ТЕМПЕРАТУРЫ ТРУДНОДОСТУПНОЙ ДЛЯ ИЗМЕРЕНИЯ

Аннотация

Разработана методика определения параметров регуляризации решения граничной обратной задачи теплопроводности, возникающей при определении температуры в зоне контакта электрод - деталь, недоступной для непосредственного термометрирования при восстановлении деталей почвообрабатывающих машин с помощью электроконтактного нагрева.

Ключевые слова: температура, алгоритм, труднодоступной.

Телгожаева F.S.

Master, KazNU named after al-Farabi Kazakh national University, Kazakhstan

OPTIMIZATION METHOD FOR DETERMINATION OF THE TEMPERATURE OF THE HARD-TO-REACH FOR THE MEASUREMENT OF

Abstract

The method was developed for determining the parameters of the regularization of solutions of inverse boundary value problem of heat conduction, which occurs in the definition of temperature in the zone of contact of the electrode - part, inaccessible for direct термометрирования when restoring parts of soil-cultivating machines with the help of electro contact heating.

Keywords: temperature, algorithm, hard-to-reach.

Рассмотрим задачу определения температуры поверхности труднодоступной для измерения. Найти  - из соотношений:                                          

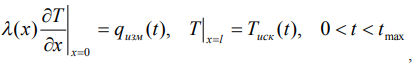 (3) по известной дополнительной информации: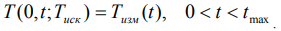                        

Пусть 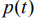 - приближенное решение обратной задачи. Рассмотрим функционал:

.                                       (4)                            

Пусть известно приближение 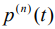. Последующие приближения определим из:

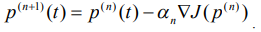                                    (5)

Здесь: 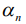 - коэффициент спуска, который определяется из условия: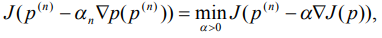  - градиент функционала.

Получим формулы для градиента функционала, по аналогии как в работе [1].

Зададим приращения: 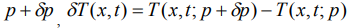. Приращение функционала, имеет вид:     

.         

Для приращения  имеем следующую задачу:

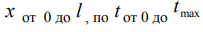Далее умножим обе части уравнения (7) на функцию  и проинтегрируем по  имеем:                      

                   (10)

Обозначим левую часть через 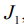 а правую часть через  и применяя интегрирование по частям, получим выражение: 

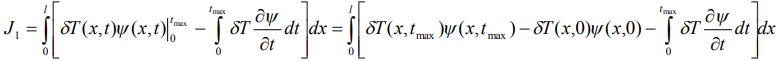
Учитывая, условия (8) и полагая что:

                                                      (11)

получим:  .

Далее проведем аналогичные выкладки для . Учитывая условия (8), (9) и полагая:

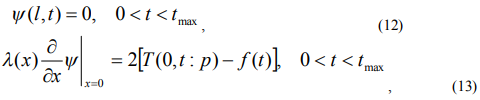
соотношение для , примет вид:

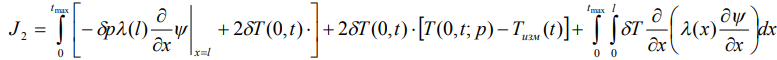
В результате соотношение (10) примет вид:

Полагая, что имеет место

                  (14)

получим, окончательно:     

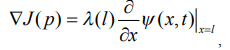                                                                 (15)

где - решения сопряженной задачи (11)-(14).

Алгоритм решения оптимизационной задачи выглядит так:

1⁰  Зададим начальные приближение 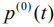, и решим прямую задачу (1)-(3), получим

2⁰  Вычислим краевое условие (13) и решая сопряженную задачу получим

3⁰    Вычислим градиент функционал (15), получим .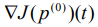

4⁰   Очередное приближение 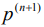, вычисляем по формуле (5)

5⁰     Проверяем значение функционала (4). Если он достиг минимума, то задача решена.