КОРРЕЛЯЦИОННО-СПЕКТРАЛЬНАЯ ОБРАБОТКА РАДИОИМПУЛЬСОВ

Пахотин В.А.¹, Гюлумян Д.К.², Рудниченко В.В.³

¹Доцент физико-математических наук; ²магистрант; ³магистрант, Балтийский федеральный университет им. И. Канта

КОРРЕЛЯЦИОННО-СПЕКТРАЛЬНАЯ ОБРАБОТКА РАДИОИМПУЛЬСОВ

Аннотация

 Рассмотрена возможность совместной корреляционно-спектральной обработки радиоимпульса. Выведены выражения, определяющие оптимальный алгоритм обработки, приведены выражения для дисперсии параметров радиоимпульса.

Ключевые слова: корреляционно-спектральная обработка, дисперсия, метод максимального правдоподобия.

Pahotin V.A.¹, Gjulumjan D.K.², Rudnichenko V.V.³

¹Associate professor; ²master student; ³master student, Immanuel Kant Baltic federal university

CORRELATION-SPECTRAL PROCESSING OF RADIO PULSES

Abstract

The possibility of joint correlation and spectral processing of the radio pulse was reviewed. Expressions determining the optimal processing algorithm were derived, expressions for the variance parameters of the radio pulse were given.

Keywords: correlation and spectral processing, dispersion, the method of maximum likelihood.

Введение

Одной из главных задач в радиотехнических комплексах аппаратуры является задача оценки параметров. Для отдельных радиоимпульсов  она решается с помощью корреляционного или спектрального анализа. Корреляционный анализ позволяет оценить комплексную амплитуду радиоимпульса и его время приема. Спектральный анализ позволяет оценить комплексную амплитуду радиоимпульса и его частоту. Однако в радиотехнических комплексах аппаратуры часто требуется оценка, как частоты радиоимпульса, так и времени приема. Например, в радиолокации время приема радиоимпульса определяет дальность до цели , а доплеровский сдвиг частоты определяет радиальную скорость движения цели. В связи с этим необходима методика совместного корреляционно – спектрального анализа, позволяющего оценивать по существу все параметры принятого радиоимпульса. Существующие возможности микроэлектроники вполне достаточны для создания программируемых радиоплат, реализующих фактически в режиме реального времени алгоритмы корреляционно-спектрального анализа вместо широко известных микросхем  быстрого преобразования Фурье (БПФ). В связи с этим в настоящей работе  рассмотрена методика совместного корреляционно-спектрального анализа радиоимпульса на основе положений теории оптимального приема.

Основы теории

Для проведения корреляционно-спектральной обработки радиоимпульса  запишем сигнал в виде

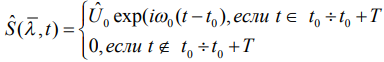                                               (1)

где 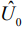 - комплексная амплитуда сигнала, 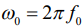– круговая частота,

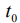– время приема радиоимпульса,

– длительность радиоимпульса,

- вектор параметров сигнала.

       Запишем принятое сообщение в виде:

                                                                                                      (2)

где 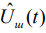– аддитивный гауссовский шум с дисперсией , средним значением, равным нулю, и интервалом корреляции .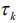

Запишем на основании (2) логарифм функции правдоподобия:

                                                           (3)

где штрихами определены оценочные параметры сигнала.

Дифференцируя логарифм функции правдоподобия по оценочной амплитуде  и приравнивая дифференциал нулю,  можно получить уравнение правдоподобия, которое дает оценку амплитуды.

 

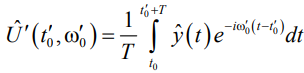                                                 (4)

Амплитуда 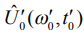 зависит от двух переменных и  представляет собой двумерную поверхность. Ее вид показан на рис.1.

Рис. 1 – Двумерная корреляционная функция: частота  (кГц) - время приема (мкс). Отношение сигнал/шум = 20 дБ.

Математическое ожидание от выражения (4) представляет собой корреляционную функцию.

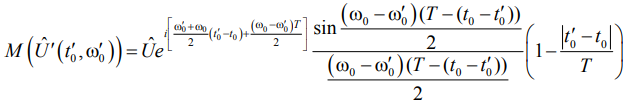        (5)

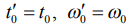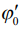В точке максимума  математическое ожидание оценочной амплитуды  равно амплитуде сигнала . Следовательно, решение несмещенное. Максимум двумерной корреляционной функции обеспечивает оценку всех параметров радиоимпульса:  амплитуды  , начальной фазы  , времени приема  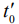 , частоты 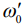. При условии  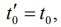выражение (5) преобразуется в амплитудно- частотный спектр, ширина которого определяется длительностью радиоимпульса  .

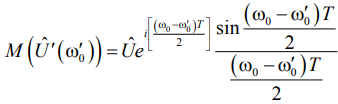                               (6)

При условии  выражение (5) преобразуется в известную корреляционную функцию радиоимпульса.

 

                                (7)

Подставляя решение (4) в функционал правдоподобия можно исключить зависимость функционала от комплексной амплитуды.

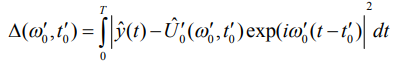                    (8)

Возведем данное выражение в квадрат и преобразуем. В результате получим.

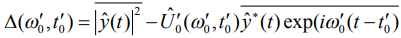                  (9)

Черта сверху означает интегрирование по времени.

Функционал (8) представляет собой поверхность, минимум которой определяет дисперсию шума 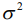 (на основании (3)). Использование минимума  функционала правдоподобия (8) предпочтительнее по сравнению с функцией корреляции (4). Если ширина двумерной  корреляционной функции (4) зависит от длительности радиоимпульса , то ширина двумерного функционала (8) зависит лишь от отношения сигнал/шум. На рис.2 показана поверхность обратного функционала  .

Рис. 2 – Обратный функционал 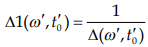 на двумерной плоскости частота (кГц) - время приема радиоимпульса (мкс).

Отношение сигнал/шум=20 дБ. Количество некоррелированных отсчетов 75.

Значение обратного функционала 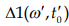   в максимуме является определенным критерием для оценки получаемого решения.

 Чем больше значение обратного функционала в максимуме, тем достовернее и точнее получаемые оценки параметров радиоимпульса. Корреляционная функция (4) или функционал правдоподобия (8)  позволяют оценить энергию сигнала 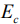 и энергию шума

                           (10)

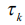- определяется полосой пропускания выходного блока  приемника.

Это позволяет по полученным данным решить задачу обнаружения радиоимпульса. Вероятность обнаружения определяется выражением.

                       (11)

Где 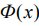- функция ошибок, - количество некоррелированных отсчетов шума на интервале .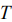

Метод максимального правдоподобия позволяет получить новое решение. Если логарифм функции правдоподобия продифференцировать по оценочной частоте 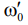 и приравнять дифференциал нулю, то можно получить.

.                           (12)

По своей структуре выражения (4) и (12) различны. Выражение (4) определяет при неизвестных параметрах спектральную и корреляционную функцию совместно. Выражение (12) определяет  корреляционную функцию и  спектральную функцию с весом. Весовая добавка 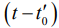 определяет ценность отсчетов для оценки частоты. В области 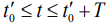ценность информации при обработке различна. Она минимальна вблизи  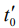и максимальна при  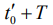.  Следовательно, оценка частоты более точная, если проводить обработку согласно (12).

Оценим дисперсии параметров радиоимпульса при корреляционно- спектральной обработке. Для этого согласно [1,2,3] определим элементы информационной матрицы Фишера, дифференцируя логарифм функции правдоподобия по параметрам сигнала.

                                            (13)

Диагональные элементы матрицы, обратной матрице Фишера, определяют дисперсии параметров радиоимпульса.

Амплитуда и начальная фаза радиоимпульса являются независимыми параметрами. Их дисперсии находятся отдельно.

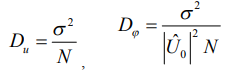                                    (14)

Для оценки дисперсии времени приема и частоты определим дифференцированием двумерную информационную матрицу Фишера

                                                    (15)

 Диагональные элементы обратной матрицы определяют дисперсии.

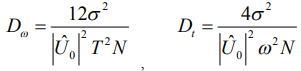                      (16)

По сравнению с аналогичными оценками дисперсии [1,2] при раздельном корреляционном или спектральном анализе дисперсии согласно (16) увеличились в 4 раза. Это результат отсутствия информации о частоте и времени приема при совместной корреляционно-спектральной обработке сигнала. Дисперсия частоты в значительной степени определяется длительностью радиоимпульса . При малых длительностях радиоимпульса дисперсия частоты значительная. Для дисперсии времени приема выражение (16) показывает явную зависимость от частоты. В настоящее время дисперсия времени приема оценивается не выражением (16), а формулой Вудворда [1,2].Для радиоимпульса она может быть записана в виде

                                             (17)

Формула Вудворда определяет дисперсию по огибающей радиоимпульса, выражение же (16) получено согласно формуле Рао-Крамера при известной фазе сигнала. Зависимости (16) и (17) существенно различаются. Формула Вудворда рекомендует малые длительности импульсов , при которых дисперсия  становится малой. В формуле Рао-Крамера дисперсия 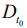 не зависит от длительности радиоимпульса , а зависит лишь от частоты.

Рис. 1.

На рис.3 показана косинусная часть корреляционной функции (4)  при     и начальной фазе радиоимпульса 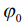, равной нулю. Различия в выражениях (16) и (17) можно понять, если алгоритм оценки  создать на основе косинусной квадратурной компоненты. При знании начальной фазы 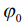, оценка дисперсии происходит по радиусу кривизны максимума основного лепестка косинусной составляющей корреляционной функции. Кривизна зависит лишь от частоты, но не зависит от длины радиоимпульса 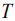. Кривизна же (наклон) огибающей зависит от длительности радиоимпульса 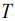. Однако использование косинусной (или синусной) составляющей корреляционной функции достаточно сложно в связи с большими боковыми лепестками. Использование же огибающей для оценки времени приема приводит к  проблеме: одновременное повышение точности оценок времени приема и частоты невозможно. При увеличении длительности радиоимпульса  точность оценки частоты возрастает (16), однако точность оценки времени приема падает (17).

Заключение

В настоящей работе на основе положений теории оптимального приема рассмотрен вопрос о совместной корреляционно-спектральной обработке радиоимпульса. Получены выражения, определяющие алгоритм оптимальной обработки радиоимпульса. Показана  вторая возможность корреляционно- спектральной обработки радиоимпульса, включающая в основное выражение   весовую обработку. При этом точность оценки частоты увеличивается. Выведены выражения, определяющие дисперсию параметров радиоимпульсов (дисперсию Рао-Крамера) при корреляционно-спектральной обработке. Обсуждаются вопросы, связанные с дисперсией времени приема радиоимпульса, полученные по выражению Рао-Крамера и по Вудворду.