ОЦЕНКА КАЧЕСТВА ПРОМЫСЛОВОЙ ОТЧЕТНОСТИ НА ОСНОВЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ

ОЦЕНКА КАЧЕСТВА ПРОМЫСЛОВОЙ ОТЧЕТНОСТИ НА ОСНОВЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ

Научная статья

Проценко И.Г.*

Камчатский государственный технический университет, Петропавловск-Камчатский, Россия

* Корреспондирующий автор (ip1954[at]list.ru)

Аннотация

Статья посвящена оценке качества промысловой отчетности в промышленном рыболовстве на основе прогностической модели процесса вылова рыбы. Оценка основана на сравнении прогностического значения улова и фактическими данными промыслового отчета. Применение математической модели позволяет уменьшить доверительный интервал ошибок отчетности и проводить эффективный контроль качества поступающих отчетных данных о вылове. Использование рекуррентных формул фильтра Калмана дает возможность реализовать вычисления в реальном масштабе времени. В совокупности, применение данного подхода обеспечит пользователей информационной рыбопромысловой системы качественной аналитической информацией.

Ключевые слова: информационная рыбопромысловая система, промысловая отчетность, авторегрессионная модель, фильтр Калмана, численные эксперименты.

ASSESSMENT OF THE QUALITY OF FISHERY ACTIVITY REPORTING BASED ON A MATHEMATICAL MODEL

Research article

Protsenko I.G.*

Kamchatka State Technical University,Petropavlovsk-Kamchatsky, Russia

* Corresponding author (ip1954[at]list.ru)

Abstract

The article discusses the assessment of the quality of fishery reporting in industrial fisheries on the basis of a predictive model of the fishing process. The assessment is based on a comparison of the predictive value of the catch yield and the actual data of the fishing report. The use of the mathematical model allows reducing the confidence interval of reporting errors and to carry out effective quality control of the incoming reporting data on the catch yield. The use of recurrent formulas of the Kalman filter makes it possible to implement calculations in real-time. Together, the application of this approach will provide users of the fishing information system with high-quality analytical information.

Keywords: information fishing system, fishery reporting, autoregressive model, Kalman filter, numerical experiments.

Отраслевая система мониторинга (ОСМ) предназначена для мониторинга водных биоресурсов на основе непрерывного наблюдения и контроля за выловом, транспортировкой и обработкой рыбы и морепродуктов [1], [2]. Решение данной задачи обеспечивается путем наблюдения за промысловой деятельностью на судах и рыболовных участках, местоположением судов и получения на этой основе косвенных показателей состояния водных биоресурсов: вылов на усилие и площади промысловых скоплений. Эти показатели позволяют оперативно отслеживать реализацию выделенных квот вылова, интенсивность промысла и его влияние на состояние рыбных запасов.

Конечной целью функционирования ОСМ является сохранение численности биоресурсов в размерах, необходимых для их воспроизводства и последующего использования в течение длительного срока. На основе поступающей в ОСМ информации формируются выходные формы и другие аналитические материалы, позволяющие решать широкий комплекс задач по управлению рыболовством, в том числе осуществлять контроль за местонахождением и промысловой деятельностью судов, следить за полнотой и достоверностью судовой промысловой отчетности и отчетности, поступающей от рыболовных участков.

Информация ОСМ является источником для органов рыбоохраны, которые проверяют правильность ведения отчетности, контролируют соответствие результатов промысла выделенным квотам.

Основными данными в ОСМ являются результаты промысловых операций, выраженные в объемах выловленной рыбы – отчет – сведения, которые ежесуточно передаются с промысловых судов и рыболовных участков. Источником этих сведений является промысловый журнал, который ведется на судне или участке. Помимо сведений о суточном улове и количестве рыбы, отгруженной по квитанции на транспорт или завод для дальнейшей обработки улова, в журнал заносятся более подробные сведения о промысловых операциях с указанием времени начала и окончания операции, её результатах, орудиях лова и прч.

Процесс обработки входных данных ОСМ, после того, как они поступили в центр мониторинга, включает в себя первичную обработку, в процессе которой выполняется преобразование формата исходных данных во внутренний формат информационной системы, комплексный анализ, выполняющий синтаксический и семантических разбор данных и подготовка аналитического материала, ввод в базу данных, рассылка информации другим пользователям [3].

Проверка данных, поступающих в ОСМ необходима, так как встречаются ошибки случайного и умышленного характера, когда пользователь ВБР хочет скрыть реальную цифру вылова. Несмотря на то, что ошибки в основном не умышленные, факты браконьерства ещё имеют место на промысле.

Контроль объема вылова [4] – сложная задача, т.к. величина улова зависит от многих причин: состояние сырьевой базы, погодные условия, технологические особенности судна или участка и может меняться от нуля до максимальной в производственном смысле величины (т.е. зависит от производительности оборудования обработки сырца). Поэтому к величине вылова, который указан в отчете, устанавливается доверительный интервал, в который величина улова должна с высокой вероятность укладываться. В общем случае, как это выше упоминалось, в доверительный интервал входят все возможные значения вылова, что на практике снижает эффективность контроля за отчетными данными величины улова.

Снизить доверительный интервал предлагается за счет использовании математической модели расчета величины вылова на отчетные сутки, т.е. за счет прогноза величины улова по времени на 1 шаг вперед, после даты предыдущего отчета. Это спрогнозированное значение улова сравнивается с отчетным значением. А условием удовлетворительного качества поступившего отчета является попадание отчетного значения в доверительный интервал прогноза. Предполагается, что можно построить модель, в которой дисперсия ошибки прогноза будет меньше, чем дисперсия самого процесса, а значит и доверительный интервал будет давать эффективный контроль отчетных данных. Снизить доверительный интервал можно также за счет включения в модель отчетов с ближайших судов и рыболовных участков, так картина изменений промысловой обстановки (уловистости) имеет очевидную пространственную корреляцию.

В ОСМ тысячи судов и рыболовных участков, и понятно, что нужно построить тысячи моделей, т.к. объекты отчетности отличаются друг от друга, что в вычислительном плане не простая задача, поэтому для расчета параметров математической модели будут привлекаться эффективные алгоритмы.

Отчетную величину суточного улова на рыболовном участке -  за указанные сутки t можно рассматривать как сумму двух частей: части, являющейся функцией всех значений до выбранных суток t-1, и чисто случайной составляющей  [5]:

  (1)

 - совокупность данных вектора  до момента времени t-1 включительно; a - вектор неизвестных коэффициентов модели;  - управляющее воздействие, либо экзогенный фактор;  - последовательность независимых одинаково распределенных величин;  - детерминированная функция.

Ввод в уравнение шума  отражает допущенные погрешности при случайном или умышленном искажении величины улова, а также поиске неизвестного вида функции .

Перепишем (1) в векторно-матричном виде. Система уравнений M - для m-мерного векторного процесса :

   (2) - имеет размерность  и составляется в виде функции из компонент векторов ;

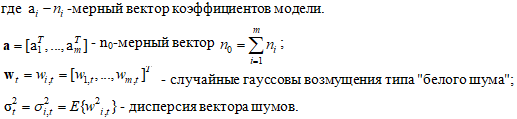
 - наблюдаемый входной вектор.

Поскольку правая часть уравнения (2) определена как шум , чтобы компенсировать недостатки модели, то естественно за счет подбора вида функции  и вектора коэффициентов модели  сделать влияние шума минимальным, а в качестве критерия выбрать минимум дисперсии шума  [6]:

  (3) Минимизация дает выражение для вектора  в виде [5]:    (4)

Расчет по формуле (4) требует необходимости запоминания всей совокупности наблюдений  до момента времени t. При мониторинге, т.е. непрерывном отслеживании динамики показателей, характеризующих процесс, необходим пересчет оценки  в новые оценки  с использованием наблюдений . Проведение подобных расчетов требует выполнения растущего с числом t количества суммирований, а при реализации на ЭВМ возрастают затраты на поиск и отбор записей наблюдений .

Можно воспользоваться алгоритмом, принадлежащим семейству алгоритмов фильтрации Калмана [7], [8], [10] и реализующем процедуру вычислений оценки коэффициентов модели в реальном масштабе времени.

Суть алгоритма, реализующего Калмановскую фильтрацию, заключается в согласовании наблюдений и физических моделей.

Введем в рассмотрение матрицу :

   (5) Оценку вектора коэффициентов модели можно записать в виде:   (6) Алгоритм вычисления оценки  можно получить исходя из описанных соотношений и представить в следующем виде:    (7) Можно вычислить оценку дисперсии шума   в реальном масштабе времени:    (8) где  - дисперсия ошибок оценивания самого процесса по модели    (9)

Алгоритм контроля входных отчетных данных выглядит следующим образом. По модели конкретного промыслового участка делается прогноз на один шаг вперед по времени (формулы 8-9) и это значения сравнивается с поступившим на эту дату отчетом о вылове. Если расхождение укладывается в доверительный интервал, то значит поступивший отчет скорее всего достоверен и нет причин подозревать пользователя ВБР в его искажении. Если же расхождение велико, то это прямой сигнал к проведению анализа поступивших данных на предмет их ошибочности или умышленного искажения. После исправления ошибок отчета коэффициенты модели и ковариационная матрица ошибок пересчитывается и сохраняется в базе данных.

Применение математической модели рыбопромыслового участка позволяет проводить контроль качества поступающих отчетных данных о вылове. В свою очередь, количество участков, как и количество соответствующих им моделей велико, поэтому применение рекуррентных формул фильтра Калмана весьма целесообразно. В совокупности, применение данного подхода повысит качество промысловой информации ОСМ, которая, в свою очередь обеспечит пользователей системы качественной аналитической информацией.

Конфликт интересов Не указан.

Conflict of Interest None declared.

Список литературы / References

1. Проценко И.Г. Информационная система мониторинга рыболовства / И.Г. Проценко // Рыбное хозяйство, 2001. Спец. выпуск. С.3-18.
2. Мониторинг рыболовства 2005. Инструкции и рекомендации экипажам промысловых судов и судовладельцам / Под общ. ред. д.т.н. Проценко И.Г., – Петропавловск-Камч.: ФГУП "Камчатский центр связи и мониторинга", 2005. – 264 с.
3. Проценко И.Г. Оптимизация обработки входной информации в отраслевой системе мониторинга рыболовства/ И.Г. Проценко //Международный научно-исследовательский журнал, №8(86)/2019.Часть 1,Август,Екатеринбург.
4. Кошкарева Л.А. Алгоритм контроля расхода сырца при выпуске рыбной продукции на основе данных промысловой отчетности / Л.А. Кошкарева // Материалы международных научных чтений «Приморские зори – 2005». Владивосток: ТАНЭБ, 2005. – 286 с. Выпуск второй.
5. Кашьяп Р.Л. Построение динамических стохасти­ческих моделей по экспериментальным данным / Р.Л. Кашьяп, А.Р. Рао. Пер. с англ.,- М.: Наука, 1983.
6. Epstein Ed. S. Stochastik dynamik prediction / Ed. S. Epstein // Tellus, v.21, N6, p.739-759, 1969.
7. Калман Р.Л. Очерки по математической теории систем / Р.Л. Калман, Фалб., М. Арбиб. М.: Мир, 1971.
8. Браммер К. Фильтр Калмана-Бьюси / К. Браммер, Г. Зиффлинг. М.: Наука, 1982. [Электронный ресурс] - URL: https://www.twirpx.com/file/21556/ (дата обращения: 12.03.2021)
9. Kalman R.E. New methods in Wiener filtering theory / R.E. Kalman // In: Proc.Symp.Eng.Appl.Random Functious - New York: Wiley, 1963.
10. Petersen D. P. On the concept and implementation of sequential analylis for linear random fields / D. P. Petersen // Tellis, v. 20, N 4, p. 673-686, 1968.

Список литературы на английском языке / References in English

1. Protsenko I. G. Informacionnaja sistema monitoringa rybolovstva [Information System for Monitoring Fisheries] / I. G. Protsenko // Rybnoe khozyaistvo [THE FISHERIES JOURNAL], 2001. Special issue, pp. 3-18 [in Russian]
2. Fisheries Monitoring 2005 Instrukcii i rekomendacii ehkipazham promyslovykh sudov i sudovladel'cam [Instructions and Recommendations to the Crews of Fishing Vessels and Shipowners]. Edited by Protsenko I. G., Doctor of Engineering Sciences - Petropavlovsk-Kamchatsky.: Federal State Unitary Enterprise "Kamchatka Center for Communication and Monitoring", 2005. - 264 p. [in Russian]
3. Protsenko I. G. Optimizacija obrabotki vkhodnojj informacii v otraslevojj sisteme monitoringa rybolovstva [Optimization of Processing Input Information in the Industrial Fisheries Monitoring System] / I. G. Protsenko // Mezhdunarodnyjj nauchno-issledovatel'skijj zhurnal [International Research Journal], No. 8 (86)/2019.Part 1, August, Yekaterinburg, ISSN 2227-6017 (ONLINE), ISSN 2303-9868 (PRINT), DOI:10.18454/IRJ.2227-6017.PI No. FS 77-51217, 16+ [in Russian]
4. Koshkareva L. A. Algoritm kontrolja raskhoda syrca pri vypuske rybnojj produkcii na osnove dannykh promyslovojj otchetnosti [Algorithm for Monitoring the Consumption of Raw Materials in the Production of Fish Products Based On the Data of Commercial Reporting] // Materialy mezhdunarodnykh nauchnykh chtenijj «Primorskie zori – 2005». [Proceedings of the International Scientific Readings "Primorskie Zori - 2005"]. Vladivostok: TANEB, 2005 – 286 p. Issue two. [in Russian]
5. Kashyap R. L. [Construction of Dynamic Stochastic Models Based On Experimental Data] / R. L. Kashyap, A. R. Rao // Translation from English, - M.: Nauka, 1983 [in Russian]
6. Epstein Ed. S. Stochastik dynamik prediction / Ed. S. Epstein // Tellus, v.21, N6, p.739-759, 1969.
7. Kalman R. L. Ocherki po matematicheskoj teorii sistem [Essays on the mathematical theory of systems] / R. L. Kalman, P. Falb, M. Arbib. Moscow: Mir, 1971 [in Russian]
8. Brammer K. Fil'tr Kalmana-B'jusi [The Kalman-Bucy Filter] / K. Brammer, G. Siffling // Moscow: Nauka, 1982. [Electronic resource] - URL: https://www.twirpx.com/file/21556/ (accessed: 12.03.2021) [in Russian]
9. Kalman R.E. New methods in Wiener filtering theory / R.E. Kalman // In: Proc.Symp.Eng.Appl.Random Functious - New York: Wiley, 1963.
10. Petersen D. P. On the concept and implementation of sequential analylis for linear random fields / D. P. Petersen // Tellis, v. 20, N 4, p. 673-686, 1968.