СВОБОДНЫЕ КОЛЕБАНИЯ ОСЕСИММЕТРИЧНЫХ ОБОЛОЧЕЧНЫХ КОНСТРУКЦИЙ

СВОБОДНЫЕ КОЛЕБАНИЯ ОСЕСИММЕТРИЧНЫХ ОБОЛОЧЕЧНЫХ КОНСТРУКЦИЙ

Научная статья

Латухин А.Ю.¹, Латухина Ю.А.^2, *

^{1, 2} Нижегородский государственный технический университет Дзержинский политехнический институт (филиал), Дзержинск, Россия

* Корреспондирующий автор (julia[at]dzerginsk.ru)

Аннотация

В статье рассматривается задача о свободных колебаниях осесимметричных оболочечных конструкций, представляющих собой произвольную композицию оболочек вращения и круговых пластин. Отдельные оболочки вращения (подконструкции) могут быть выполнены из различных изотропных линейно-упругих материалов с переменными вдоль образующей геометрическими характеристиками. В данной работе разработана методика для численного решения обобщенной проблемы на собственные значения, которая возникает при рассмотрении задач расчета на прочность оболочечных конструкций.

Ключевые слова: колебания, осесимметричная конструкция, тонкостенная конструкция.

FREE OSCILLATIONS OF AXISYMMETRIC SHELL STRUCTURES

Research article

Latukhin A.Yu.¹, Latukhina Yu.A.^2, *

^{1, 2} Nizhny Novgorod State Technical University Dzerzhinsk Polytechnic Institute (branch), Dzerzhinsk, Russia

* Corresponding author (julia[at]dzerginsk.ru)

Abstract

The paper considers the problem of free oscillations of axisymmetric shell structures, which are an arbitrary composition of shells of revolution and circular plates. Separate shells of rotation (substructure) can be made of various isotropic linearly elastic materials with variable geometric characteristics along the generatrix. In this paper, the authors have developed a technique for numerically solving a generalized eigenvalue problem that arises when considering the problems of calculating the strength of shell structures.

Keywords: vibrations, axisymmetric construction, thin-walled construction.

Введение

Оболочечные конструкции, имея высокие прочностные характеристики и малый вес, широко используются в различных областях техники. Рост требований, предъявляемых к надежности оболочечных конструкций, приводят к необходимости создания методик, позволяющих решать задачи расчета на прочность, которые возникают при проектировании оболочечных конструкций.

Одной из подобных задач прочности оболочечных конструкций является задача определения параметров свободных колебаний.

Уравнения, описывающие свободные колебания тонкостенной конструкции, можно сформулировать на основе принципа виртуальной работы совместно с принципом Даламбера [2], [3], [4]:

    (1)

где V – объем тела; – тензор напряжений;  – тензор деформаций; p – плотность материала;  – поле перемещений, удовлетворяющее заданным кинематическим граничным  условиям;  – поле ускорений; δ –кинематически возможные вариации соответствующей величины.

Рассмотрим оболочку вращения, срединная поверхность которой образована вращением некоторой плоской кривой F(x) вокруг оси OX.

Положение точки на поверхности вращения определяется криволинейными ортогональными координатами α₁ и α₂, отсчитываемыми соответственно вдоль меридиана и параллели. В этом случае коэффициенты Ламе A₁ и A₂ и главные радиусы кривизны R₁ и R₂ не зависят от координаты α₂. Координату z, определяющую расстояние от некоторой точки оболочки до срединной поверхности, определим таким образом, чтобы система координат (α_1,α_{2, z}) образовывала правую ортогональную систему координат.

Так как оболочка вращения находится в условиях осесиммметричной деформации, то все параметры напряженно-деформированного состояния не зависят от координаты α₂.

Предполагается, что для оболочки вращения справедливы гипотезы Кирхгофа-Лява [7].

Тогда компоненты тангенциальной  и изгибной  деформаций срединной поверхности оболочки вращения, находящейся в условиях осесимметричной деформации, можно записать в следующем виде [7]:

   (2)

где u, w – перемещения срединной поверхности в направлении α₁ и z соответственно; Θ – угол поворота нормали к срединной поверхности вокруг направления α₂.

    (3)

Компоненты перемещения и деформации произвольной точки оболочки, отстоящей на расстоянии z от срединной поверхности, определяются по формулам:

    (4) Физические соотношения, устанавливающие связь между напряжениями и деформациями, записываются в виде [7]:     (5)

где E – Модуль Юнга; v – коэффициент Пуассона.

Введем усилия и моменты, действующие в осевом и окружном направлениях: нормальные усилия  и изгибающие моменты . Внутренние усилия и моменты приводятся к срединной поверхности оболочки и определяются по формулам:

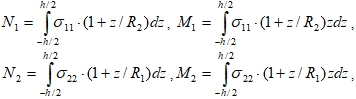   (6)

где h – толщина оболочки.

Используя соотношения (4) и (5), выполняя в формулах (6) интегрирование по толщине оболочки и пренебрегая членами порядка , получаем:

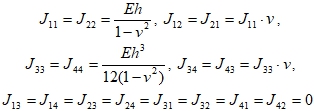    (7) Коэффициенты жесткости  оболочки, определяются из выражений:    (8)

С учетом приведенных геометрических и физических соотношений преобразуем вклад n-й подконструкции в исходное вариационное уравнение (1).

Вариация внутренней энергии отдельной оболочки вращения, находящейся в условиях осесимметричной деформации, может быть записана в следующем виде:

 (9)

Используя геометрические соотношения (4), выполняя интегрирование по толщине в выражении (9) с учетом (6) и (7), получаем

   (10)

где  – вектор деформаций срединной поверхности; [J] – квадратная матрица размерности 4 x 4 с компонентами , выражения которых даны соотношениями (8).

В соответствии с характером деформирования оболочки, определяемыми гипотезами Кирхгофа-Лява, инерционные силы путем интегрирования по толщине могут быть приведены к системе распределенных по срединной поверхности инерционных обобщенных сил: .

Таким образом, вариация работы инерционных сил, действующих на отдельную симметрично нагруженную оболочку вращения может быть записана следующим образом:

    (11)

где  – вектор обобщенных перемещений срединной поверхности;  – вектор обобщенных ускорений;  – диагональная квадратная матрица размером 3 x 3 с компонентами.

Объединяя (10) и (11) получим вклад n-й подконструкции в исходное уравнение

    (12) После этого исходное вариационное уравнение можно записать:    (13) где N – количество подконструкций, входящих в состав тонкостенной конструкции.

Дискретизация исходного вариационного уравнения (1) по пространственной переменной осуществляется на основе метода конечных элементов. Тонкостенная осесимметричная конструкция условно расчленяется на N подконструкций, которые, в свою очередь, набираются из отдельных конечных элементов.

Согласно принятой численной схеме исходное вариационное уравнение (1) может быть записано в виде:

   (14)

где  – вклад одного конечного элемента с индексом s подконструкции n:

   (15)

В качестве конечного элемента выбран элемент тонкой усеченной конической оболочки с линейным и кубическим законами распределения тангенциальных u и нормальных w перемещений срединной поверхности соответственно.

Этот конечный элемент имеет шесть граничных степеней свободы, удовлетворяет условиям совместности и учитывает смещения тела как жесткого целого.

В соответствии с конечно-элементной техникой дискретизации выразим вектор обобщенных перемещений срединной поверхности конечного элемента через его узловые перемещения :

    (16)

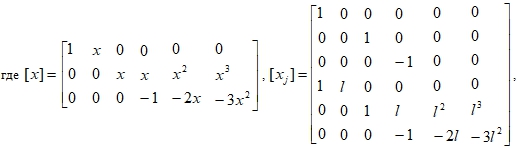
  – длина образующей конечного элемента.

Аналогичным образом выражаются векторы обобщенных скоростей и ускорений срединной поверхности конечного элемента:

   (17) Геометрические соотношения для элемента конической оболочки получаются из зависимостей (2), если положить   Тогда с учетом (16) имеем:     (18) Где  

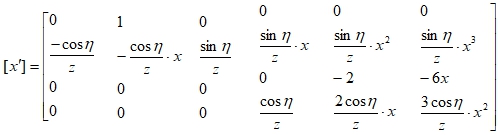
Физические соотношения, устанавливающие связь внутренних усилий и моментов с деформациями срединной поверхности конечного элемента, записываются согласно (7) и (16):

    (19)

С учетом введенных конечно-элементных аппроксимаций вклад отдельного конечного элемента (1.15) в исходное вариационное уравнение (1) может быть представлен в виде:

где  – матрица массы и жесткости конечного элемента:

   (20)    (21)

При этом предполагается, что компоненты матриц [p], [J] и координата z изменяются вдоль образующей конечного элемента по линейному закону:

 

где нижний индекс у величин означает принадлежность соответствующему узлу конечного элемента.

Вычисление интегралов (20) и (21) осуществляется численно с помощью квадратурной формулы Гаусса [3,8].

Выражения (20) и (21) для матрицы массы и жесткости получены для отдельных конечных элементов, не связанных какими-либо условиями с соседними элементами. Объединение их на уровне подконструкции требует выполнения условий совместности ускорений и перемещений по границам смежных элементов. Для этого необходимо произвести переход от местной системы координат (Oxz) к глобальной (OXZ). Это преобразование осуществляется с помощью соотношений:      (22)

После подобного преобразования вклад отдельного конечного элемента в исходное вариационное уравнение (1) запишется в виде:

    (23)

где [m], [k] – матрицы массы и жесткости конечного элемента в глобальной системе координат:

    (24)

Последовательное объединение вкладов отдельных конечных элементов, входящих в состав n-й подконструкции, с учетом общих перемещений в узлах соседних элементов, а затем вкладов подконструкций с учетом общих перемещений по их границам приводит к дискретным уравнениям, описывающим свободные колебания оболочечных конструкций:

    (25)

где [M], [K] – матрицы массы и жесткости конструкции;  – векторы обобщенных узловых ускорений и перемещений конструкции.

Математически (25) представляют собой систему линейных однородных обыкновенных дифференциальных уравнений второго порядка с постоянными коэффициентами.

Решение системы (25) может быть записано в виде:

     (26)

где  – вектор формы свободных колебаний конструкции; ω – угловая частота свободных колебаний; t – время; t₀ – начальная фаза.

Подставляя (26) в (25), получаем обобщенную проблему на собственные значения:

    (27)

Решение задачи нахождения частот и форм свободных колебаний в заданном диапазоне частот осуществляется численно с помощью методов, основанных на делении спектра матрицы и решении характеристического уравнения, в сочетании с методом обратных итераций со сдвигом.

Численное решение обобщенной проблемы на собственные значения (27) осуществляется по следующей схеме:

1. на первом этапе определяется число собственных частот, расположенных в заданном диапазоне частот; реализация этого этапа опирается на теорему [1], [4], которая утверждает:

Если матрица  допускает разложение , где  – нижняя треугольная матрица с единицами на главной диагонали,  – диагональная матрица, то количество собственных значений, меньших , равно числу отрицательных элементов матрицы ;

2. на втором этапе производится локализация частот свободных колебаний, т.е. находятся левая и правая границы интервалов, внутри каждого из которых лежит единственная частота;
3. на третьем этапе осуществляется уточнение каждой частоты свободных колебаний ω в рассматриваемом диапазоне частот и соответствующей ей формы колебаний 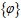 с помощью метода обратных итераций со сдвигом.

Заключение

В данной работе разработана методика для численного решения обобщенной проблемы на собственные значения. Численная методика используется для решения задачи нахождения частот и форм свободных колебаний в заданном диапазоне частот тонкостенных конструкций, представляющих собой произвольную композицию оболочек вращения в условиях осесимметричной деформации.

На модельных задачах выполнен ряд расчетов по определению параметров свободных колебаний некоторых элементов оболочечных конструкций. Сопоставление полученных результатов с имеющимися в литературе аналитическими решениями показывает их хорошее соответствие.

Конфликт интересов Не указан.

Conflict of Interest None declared.

 

Список литературы / References

1. Бате К. Численные методы анализа и метод конечных элементов: Пер. с англ / Бате К., Вилсон Е. – М.: Мир, 1982. – 448 с., ил.
2. Новожилов В.В. Теория тонких оболочек / Новожилов В.В. – Л.: Судпромгиз, 1951. – 344с.
3. Демидович Б.П. Основы вычислительной математики / Демидович Б.П., Марон И.А. – М.: Физматгиз, 1963. – 660 с., ил.
4. Воеводин В.В. Матрицы и вычисления / Воеводин В.В., Кузнецов Ю.А. – М.: Наука. Гл. ред. физ.-мат. лит., 1984. – 320 с.
5. Годунов С.К. Лекции по современным аспектам линейной алгебры / Годунов С.К. – Новосибирск: Научная книга (ИДМИ), 2002. – 216 с., ил.
6. Голуб Дж., Матричные вычисления: Пер. с англ / Голуб Дж., Ван Лоун Ч. – М.: Мир, 1999. – 548 с., ил.
7. Джордж .А. Численное решение больших разреженных систем уравнений: Пер. с англ / Джордж .А, Лю Дж. – М.: Мир, 1984. – 333 с., ил.
8. Икрамов Х.Д. Численные методы для симметричных линейных систем / Икрамов Х.Д. – М.: Наука. Гл. ред. физ.-мат. лит., 1988. – 100 с.
9. Каханер Д.Численные методы и программное обеспечение: Пер. с англ. / Каханер Д., Моулер К., Нэш С. – Изд. второе стереотип. – М.: Мир, 2001. – 575 с., ил.
10. Молчанов И.Н. Основы метода конечных элементов / Молчанов И.Н., Николаенко Л.Д. – Киев: Наук. думка, 1989. – 272 с.
11. Писсанецки С. Технология разреженных матриц: Пер. с англ. / Писсанецки С. – М.: Мир, 1988. – 410 с., ил.
12. Райс Дж. Матричные вычисления и математическое обеспечение: Пер. с англ. / Райс Дж. – М.: Мир, 1984. – 264 с., ил.

Список литературы на английском языке / References in English

1. Bate K. Chislennyye metody analiza i metod konechnykh elementov [Numerical analysis methods and finite element method]: Trans. from English / Bate K., Wilson E. – M.: Mir, 1982. – 448 p., Ill. [in Russian]
2. Novozhilov V.V. Teoriya tonkikh obolochek [Theory of thin shells] / Novozhilov V.V. – L.: Sudpromgiz, 1951. – 344 p. [in Russian]
3. Demidovich B.P. Osnovy vychislitel'noy matematiki [Fundamentals of Computational Mathematics] / Demidovich B.P., Maron I.A. – M.: Fizmatgiz, 1963. – 660 p., Ill. [in Russian]
4. Voevodin V.V. Matritsy i vychisleniya [Matrices and calculations] / Voevodin V.V., Kuznetsov Yu.A. – M.: Science. Ch. Ed. Phys.-Math. lit., 1984. – 320 p. [in Russian]
5. Godunov S.K. Lektsii po sovremennym aspektam lineynoy algebry [Lectures on modern aspects of linear algebra] / Godunov S.K. – Novosibirsk: Scientific Book (IDMI), 2002. – 216 p., Ill. [in Russian]
6. Golub J. Matrichnyye vychisleniya [Matrix calculations] / Golub J., Van Lone C. // Trans. from English – M.: Mir, 1999. – 548 p., Ill. [in Russian]
7. George A. Chislennoye resheniye bol'shikh razrezhennykh sistem uravneniy [Numerical solution of large sparse systems of equations]: Trans. from English / George A., Liu J. – M.: Mir, 1984. – 333 p., Ill. [in Russian]
8. Ikramov H.D. Chislennyye metody dlya simmetrichnykh lineynykh sistem [Numerical methods for symmetric linear systems]. / Ikramov H.D. – M.: Science. Ch. ed. Phys.-Math. lit., 1988. – 100 p. [in Russian]
9. Kahaner D. Chislennyye metody i programmnoye obespecheniye [Numerical methods and software] Trans. from English – 2^nd / Kahaner D., Mowler K., Nash S. – M.: Mir, 2001. – 575 p., Ill. [in Russian]
10. Molchanov I.N. Osnovy metoda konechnykh elementov [Fundamentals of finite element method] / Molchanov I.N., Nikolaenko L.D. – Kiev: Nauk. Dumka, 1989. – 272 p. [in Russian]
11. Pissanetski S. Tekhnologiya razrezhennykh matrits [Technology of sparse matrices]: Trans. from English / Pissanetski S. – M.: Mir, 1988. – 410 p., Ill. [in Russian]
12. Rice J. Matrichnyye vychisleniya i matematicheskoye obespecheniye [Matrix calculations and software]: Per. from English / Rice J. – M.: Mir, 1984. – 264 p., Ill. [in Russian]