НЕРАВНОВЕСНАЯ ТЕРМОДИНАМИКА. ТЕОРИЯ ПОЛЯ И ВАРИАЦИОННЫЕ ПРИНЦИПЫ
НЕРАВНОВЕСНАЯ ТЕРМОДИНАМИКА. ТЕОРИЯ ПОЛЯ И ВАРИАЦИОННЫЕ ПРИНЦИПЫ
Обзор
Клюева Я.И.1, Медведева Г.А.2, *
1, 2 Казанский государственный архитектурно-строительный университет, Казань, Россия
* Корреспондирующий автор (medvedevaga79[at]mail.ru)
АннотацияВ данной статье предлагается общий теоретический обзор понятий неравновесной термодинамики с точки зрения основных постулатов классической теории поля и ее вариационных принципов. Рассматривается линейная термодинамика Л. Онзагера и его принцип наименьшего рассеивания энергии. Особое внимание уделяется и другой формулировке этого принципа, сформулированного И. Дьярмати, в пространстве сил при постоянстве потоков для локального функционала. А также заостряется внимание на принципе минимума производства энтропии Пригожина.
Ключевые слова: теория поля, непрерывные системы, феноменологические уравнения, потенциалы рассеяния в энтропийном представлении.
NONEQUILIBRIUM THERMODYNAMICS. FIELD THEORY AND VARIATIONAL PRINCIPLES
Review
Klyueva Ya.I.1, Medvedeva G.A.2, *
1, 2 Kazan State University of Architecture and Engineering, Kazan, Russia
* Corresponding author (medvedevaga79[at]mail.ru)
AbstractThe article offers a general theoretical review of the concepts of nonequilibrium thermodynamics from the basic postulates of the classical field theory and its variational principles. Onsager’s linear thermodynamics and its principle of least energy dissipation are considered in the paper. Particular attention is paid to another formulation of this principle, formulated by I. Gyarmati, in the space of forces with constant flows for a local functional. The authors also focus on the principle of minimum production of Prigogin’s entropy.
Keywords: field theory, continuous systems, phenomenological equations, scattering potentials in the entropy representation.Первый закон термодинамики или закон сохранения и превращения энергии утверждает, что тепло ![]() , подводимое к системе, расходуется на совершение работы системой
, подводимое к системе, расходуется на совершение работы системой ![]() над внешними телами и на изменение внутренней энергии системы
над внешними телами и на изменение внутренней энергии системы ![]() :
:
где Т - это температура.
Что же касается неравновесных процессов в изолированной системе, то здесь второе начало термодинамики утверждает о невозможности уменьшения энтропии.
Большинство встречающихся в мире систем являются термодинамически неравновесными. Для того, чтобы использовать соотношение типа (2) вводится такой принцип, как локальное равновесие. Последний постулирует о сохранении условия равновесия в элементарных объемах системы при переходи её во всем масштабе от равновесного к неравновесному состоянию. Т.е. предполагается справедливость уравнения Гиббса в локальной форме:
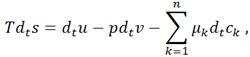 (3)
где
(3)
где 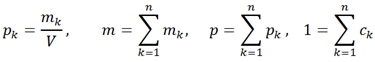
где s,u,v - удельная энтропия, внутренняя энергия и объем, m, p – масса и плотность системы, ![]()
![]() - удельная массовая концентрация, плотность и масса k-ого элемента n-компонентной системы, а также интенсивные величины: T, p, - температура, давление и химический потенциал k-ого элемента.
- удельная массовая концентрация, плотность и масса k-ого элемента n-компонентной системы, а также интенсивные величины: T, p, - температура, давление и химический потенциал k-ого элемента.
При наличии в системе релаксационных процессов соотношение Гиббса нужно дополнить. Пусть в каждой точке системы происходит ɭ химических реакций, тогда
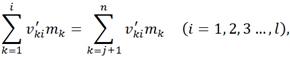
где ![]() - стехиометрический коэффициент k-ого элемента системы в i-й реакции [2], при этом
- стехиометрический коэффициент k-ого элемента системы в i-й реакции [2], при этом ![]() положителен в правой части уравнения и отрицателен в левой.
положителен в правой части уравнения и отрицателен в левой.
В каждой i-й реакции выполняется закон сохранения массы:
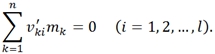
В этой связи вводится новый коэффициент ![]() , который упрощает запись локальных скоростей химических реакции в непрерывной системе:
, который упрощает запись локальных скоростей химических реакции в непрерывной системе:
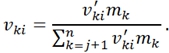
В духе принципа локального равновесия термодинамику неравновесных процессов можно рассматривать как полевую теорию и формулировать для нее законы сохранения. При этом стоит выделить два класса термодинамических систем − непрерывные и прерывные. К первому классу можно отнести системы, в которых переменные, определяющие их состояния, являются непрерывными функциями пространственных координат и времени. Второй класс состоит из нескольких подсистем, разделенных естественной и искусственной границей. Параметры состояние системы определяются только временем. Переход от одной подсистемы в другую происходит скачком.
Для непрерывных систем законы сохранения, представленный в виде локальных и субстанциональных форм, записываются в след. виде. Баланс масс:
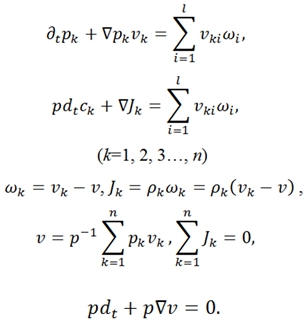 Баланс заряда:
Баланс заряда:
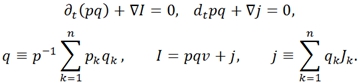 Баланс импульса:
Баланс импульса:
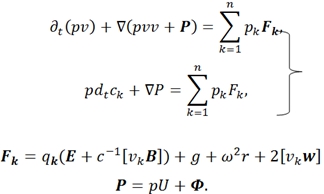 Баланс внутренней энергии:
Баланс внутренней энергии:
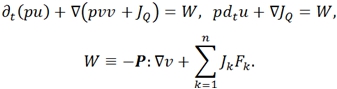 Баланс энтропии:
Баланс энтропии:
- в этих уравнениях ![]() – заряд ед. массы, скорость и диффузионный поток k-ого компонента системы; р – давление; q – полный заряд ед. массы;
– заряд ед. массы, скорость и диффузионный поток k-ого компонента системы; р – давление; q – полный заряд ед. массы; ![]() - потоки тепла и энтропии; v – скорость центра масс; Ф – тензор давления;
- потоки тепла и энтропии; v – скорость центра масс; Ф – тензор давления; ![]() – вектор внешних сил, действующих на ед. массы k-ого компонента системы; j, I – диффузионный и полные эл. поля; B – вектор магнитной индукции; r – радиус-вектор; g- ускорение свобод. падения; ω – угловая скорость системы; E – вектор напряжения эл. поля; W − источник внутренней энергии; θ − локальное производство;
– вектор внешних сил, действующих на ед. массы k-ого компонента системы; j, I – диффузионный и полные эл. поля; B – вектор магнитной индукции; r – радиус-вектор; g- ускорение свобод. падения; ω – угловая скорость системы; E – вектор напряжения эл. поля; W − источник внутренней энергии; θ − локальное производство; ![]() − оператор частной производной по времени t [1].
− оператор частной производной по времени t [1].
Построение формы баланса энтропии для конкретных термодинамических систем достигается подстановкой вышеперечисленных законов сохранения в соотношение Гиббса (3).
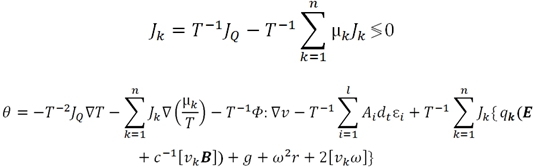
В представлении обобщенных потоков ![]() и обобщенных сил
и обобщенных сил ![]() производство энтропии имеет вид билинейной формы:
производство энтропии имеет вид билинейной формы:
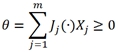 (4)
где m − число потоков (сил); (∙) − q-кратная свертка; q − ранг тензорной величины.
Энергетическое ψ описание рассевания в необратимых процессах:
(4)
где m − число потоков (сил); (∙) − q-кратная свертка; q − ранг тензорной величины.
Энергетическое ψ описание рассевания в необратимых процессах:
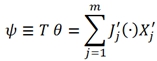 (5)
где ψ – диссипативная функция
(5)
где ψ – диссипативная функция
При условии термодинамического равновесия все силы и потоки, а также производство энтропии превращаются в нуль. В следствие с этим, при незначительном удалении от равновесия используется гипотеза Онзагера, которая устанавливает линейную связь между потоками и силами:
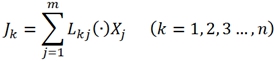 (6)
(6)
где ![]() – это обобщенные потоки и силы любой тензорной валентности; m – число независимых сил и потоков;
– это обобщенные потоки и силы любой тензорной валентности; m – число независимых сил и потоков; ![]() – тензор, декартовые компоненты которого называются феноменологическими либо кинетическими коэффициентами, либо коэффициент Онзагера.
– тензор, декартовые компоненты которого называются феноменологическими либо кинетическими коэффициентами, либо коэффициент Онзагера.
А сами соотношения (6) называются феноменологическими уравнениями или линейными уравнениями Онзагера. Они соответствуют энтропийному представлению процессов рассеивания (4).
В энергетическом представлении (5) новые феноменологические коэффициенты ![]() связаны с коэффициентом
связаны с коэффициентом ![]() соотношениями:
соотношениями:
![]() (7)
(7)
Пользуясь законом (6), можно представить энтропии θ и диссипативную функцию ψ как некоторые квадратичные формы обобщенных сил [1]:
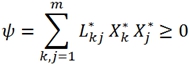
и
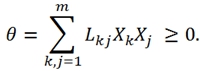
В 1931-1932 году Онзагер устанавливает важную линейную связь между кинетическими коэффициентами в отсутствие внешнего магнитного поля и вращения системы в целом в виде [2]:
Соотношения (6) и (8) составляют основу линейной термодинамики. Необходимо учитывать только то, что они справедливы в случае небольших термодинамических сил (в этом случае связь между термодинамическими потоками и силами можно считать линейной). Несмотря на то, что круг задач, решаемый с помощью этого простого формализма, является достаточно широким, встречаются примеры, где расчет с использованием соотношений (6) и (8) бывает некорректным [2].
В 1931 году Л. Онзагер предлагает вариационный принцип, из которого могут быть получены соотношения (6) и (8). Этот принцип, названный принципом наименьшего рассеивания энергии, утверждает экстремальность некоторого локального функционала, записанного в представлении варьируемых потоков J при постоянстве термодинамических сил X в виде [2]:
![]() (9)
(9)
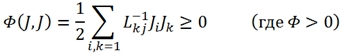 (10)
А
(10)
А 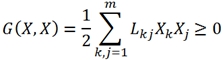 (11)
В энергетическом представлении
(11)
В энергетическом представлении С учетом (4), (9) варьируя по потокам, условие (10) можно представить в ином виде:
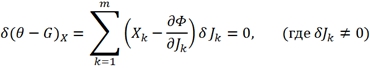 (12)
Вариационный принцип Онзагера сформулирован в пространстве термодинамических потоков. Другая формулировка этого принципа в пространстве сил при постоянстве потоков для локального функционала была дана И. Дьярмати [1].
(12)
Вариационный принцип Онзагера сформулирован в пространстве термодинамических потоков. Другая формулировка этого принципа в пространстве сил при постоянстве потоков для локального функционала была дана И. Дьярмати [1].
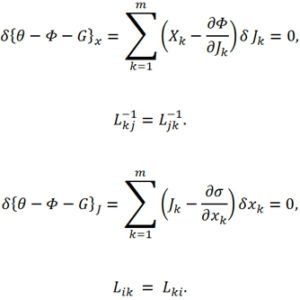
Запись является другой, если потенциалы рассеяния (10) и (11) заменены энергетическим представлением ![]() а вместо производства энтропии θ взята диссипативная функция
а вместо производства энтропии θ взята диссипативная функция ![]()
Дьярмати была также представлена интегральная форма для континуума в виде [1]:
При рассмотрении необратимых процессов в адиабатически изолированных системах, когда ![]() , форма интегрального принципа представляется в следующем виде [1]:
, форма интегрального принципа представляется в следующем виде [1]:
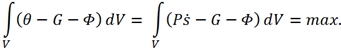 Независимо от принципа Онзагера для стационарных процессов был установлен новый принцип, называющийся принципом минимума производства энтропии. Первая формулировка для прерывных систем принадлежит Пригожину и известна в виде следующей теоремы [3]: если система поддерживается в состоянии с постоянными силами
Независимо от принципа Онзагера для стационарных процессов был установлен новый принцип, называющийся принципом минимума производства энтропии. Первая формулировка для прерывных систем принадлежит Пригожину и известна в виде следующей теоремы [3]: если система поддерживается в состоянии с постоянными силами 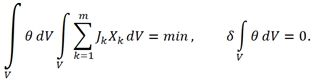 (17)
(17)
Из этого следует, что производство энтропии обладает экстремальным свойством в стационарных состояниях системы, вызванных граничными условиями. Предельным случаем стационарных состояний является равновесное состояние системы, где производство энтропии равно нулю, а энтропия максимальна.
Сравнивая формулировки принципов минимального производства энтропии и наименьшего рассеяния энергии, Дьярмати нашел между ними связь. Более того, он нашел, что принцип Пригожина является лишь эквивалентной формой принципа Онзагера на основе энтропийных представлений [2].
Рассмотрим открытые системы, находящиеся в сильно неравновесных состояниях. В них могут возникать такие структуры, которые способны к спонтанной самоорганизации, т.е. к самопроизвольному переходу от беспорядка и хаоса к упорядоченным состояниям. Пригожин назвал эти структуры диссипативными.
Примеры самоорганизации можно зафиксировать в природных и социокультурных системах. В системах неживой природы к примерам самоорганизации можно отнести: переход ламинарного течения в турбулентное, временную и пространственную упорядоченность в химических реакциях, ячейки Бенара и т. п.
Рассмотрим образование ячеек Бенара в жидкости. Если нагревать при небольших градиентах температуры не слишком толстый слой вязкой жидкости, то до определенного момента передача тепла от нижнего слоя жидкости к верхнему обеспечивается только с помощью теплопроводности [8] Однако при достижении критической разности температур нижнего и верхнего слоев система выходит из равновесия. Появляется конвекционный поток, имеющий структуру в форме правильных шестиугольных призм (конвективных ячеек). Так как система производит обмен со средой только теплом и в стационарных условиях получает такое же количество тепла, что и отдает, то можно сделать вывод, что система отдает энтропию среде, т. е. самоорганизация возникает за счет поглощения отрицательной энтропии. Стоит отметить, что подобные конвективные ячейки могут образовываться и в атмосфере, если отсутствует горизонтальный перепад давления.
В живой природе примером самоорганизации может служить первый этап создания термитами термитника [9]. На начальных этапах строительства наземного жилища термиты разбрасывают материал (частички земли) в хаотическом порядке, опрыскивая их при этом гормоном, который привлекает внимание других термитов. Вскоре число насекомых в данной точке увеличивается и вероятность сброса в этой области частичек земли растет. Так и возникают опорные стены термитника на первом этапе.
Попытки объяснения самоорганизации не обошлись стороной и в социальных сферах. Так в своих работах Адам Смит уделяет особое внимание проблемам соотношения личных и общественных интересов. По мнению мыслителя, спонтанный порядок на рынке возникает в результате взаимодействия противоположных целей и интересов участников. Его принцип «невидимой руки», гласящей об ответственность за то, чтобы конечный результат от эгоистических действий каждого индивида был полезен всему обществу в целом, и является выражением самоорганизации.
Заключение
Таким образом, исходя из проделанной работы, можно сделать вывод о том, что:
- перевод неравновесной термодинамики на язык теории поля был необходимы решением, так как многие физики только недавно стали понимать сущность необратимой термодинамики и возможность ее применения. Такой перевод был выполнен венгерским физиком Дьярмати, который сформулировал новый вариационный принцип.
- Термодинамическая формулировка этого принципа восходит к работам Л. Онзагера и Пригожина. Дьярмати объединил принципы наименьшего рассеяния и наименьшего производства энтропии, и применил этот принцип к ряду задач.
- Вариационный принцип благодаря своей простоте и физической очевидности используют многие ученые.
- Излагая неравновесную термодинамику на языке теории поля, Дьярмати в своем принципе открывает пути для решения любых задач в линейных приближениях
Следует также отметить, что среди всех научных дисциплин основное достоинство неравновесной термодинамики заключается в универсальности ее выводов, которые не привязаны к каким-либо конкретным системам. Это обстоятельство позволяет применять неравновесную термодинамику для анализа самых разных объектов живой и неживой природы, включая социальную сферу.
| Конфликт интересов Не указан. | Conflict of Interest None declared. |
Список литературы / References
- Дьярмати И. Неравновесная термодинамика. Теория поля и вариационные принципы / Дьярмати И. − М.: Мир, 1974. − 304 с.
- Журавлев В.А. Термодинамика необратимых процессов в задачах и решениях. / Журавлев В.А. − Ижевск: Издательский дом «Удмуртский университет», 1998. – 151 с.
- Пригожин. И. Введение в термодинамику необратимых процессов. / Пригожин. И − М.: Изд-во иностр. лит-ры, 1960. − 160 c.
- Био М. Вариационные принципы в теории теплообмена / Био М. − М.: Энергия, 1975. − 209 с.
- Де Гроот С.Р. Термодинамика необратимых процессов. / Де Гроот С.Р. − М.: Гос. Изд.-во техн.-теор. лит., 1956. − 280 с.
- Зубарев Д. П. Неравновесная статистическая термодинамика. / Зубарев Д. П.– М.: Наука, 1971. − 414 с.
- Новик А. Релаксационные явления в кристаллах. / Новик А., Берри Б. − М. Атомиздат, 1975 − 472 с.
- Осипов А.И. Термодинамика вчера, сегодня, завтра. Часть 2 / Осипов А.И. // Соросовский Образовательный Журнал. – М.: 1999. − № 5. − С. 91-97.
- Кочергин А.Н. Процессы самоорганизации в природных, социальных и когнитивных системах / А.Н. Кочергин // Научный вестник МГТУ ГА. – 2014. - № 203. -С. 36-42.
Список литературы на английском языке / References in English
- Gyarmati I. Neravnovesnaya termodinamika. Teoriya polya i variatsionnyye printsipy [Non-equilibrium thermodynamics. Field theory and variational principles] / I. Gyarmati − M.:Mir, 1974. – 304 p. [in Russian]
- Zhuravlev A. Termodinamika neobratimykh protsessov v zadachakh i resheniyakh. [Thermodynamics of irreversible processes in problems and solutions] / V.A. Zhuravlev − Izhevsk.: Publishing House «Udmurt University», 1998. − 151 p. [in Russian]
- I. Vvedeniye v termodinamiku neobratimykh protsessov [Introduction to the thermodynamics of irreversible processes] / I. Prigogine − M.: Publishing house of foreign literature, 1960. − 160 p. [in Russian]
- Bio M. Variatsionnyye printsipy v teorii teploobmena [ Variational principles in the theory of heat transfer]/ M. Bio − M.: Energy, 1975. − 209 р. [in Russian]
- Groot R. Termodinamika neobratimykh protsessov [Thermodynamics of irreversible processes] S. R. Groot − M.: State Publishing House of Technical and Theoretical Literature., 1956. − 280 p. [in Russian]
- Zubarev D.P. Neravnovesnaya statisticheskaya termoddinamika [Nonequilibrium statistical thermodynamics]/ D. P. Zubarev − M .: Nauka, 1971. − 414 p. [in Russian]
- Novik A. Relaksatsionnyye yavleniya v kristallakh [Relaxation phenomena in crystals] / A. Novik, B. Berry − M .: Atomizdat, 1975. − 472 р. [in Russian]
- Osipov A.I. Termodinamika vchera, segodnja, zavtra [Thermodynamics of yesterday, today and tomorrow]. Chast' 2 / A.I. Osipov // Sorosovskij Obrazovatel'nyj Zhurnal [Soros Educational Journal] − 1999. − № 5. − P. 91-97. [In Russian]
- Kochergin A.N. Protsessy samoorganizatsii v prirodnykh, sotsial'nykh i kognitivnykh sistemakh [Processes of self-organization in natural, social and cognitive systems.] / A.N. Kochergin // Civil Aviation High Technologies. −2014. − № 203.− P. 36-42. [in Russian]
