ЭФФЕКТИВНОСТЬ ТОРМОЖЕНИЯ ПОЛОЖИТЕЛЬНО И ОТРИЦАТЕЛЬНО ЗАРЯЖЕННЫХ ЧАСТИЦ В УЛЬТРАХОЛОДНОМ ГАЗЕ ЗАМАГНИЧЕННЫХ ЭЛЕКТРОНОВ

ЭФФЕКТИВНОСТЬ ТОРМОЖЕНИЯ ПОЛОЖИТЕЛЬНО И ОТРИЦАТЕЛЬНО ЗАРЯЖЕННЫХ ЧАСТИЦ В УЛЬТРАХОЛОДНОМ ГАЗЕ ЗАМАГНИЧЕННЫХ ЭЛЕКТРОНОВ

Научная статья

Бобров А.А.*

Объединенный институт высоких температур Российской академии наук, Москва, Россия

* Корреспондирующий автор (abobrov[at]inbox.ru)

Аннотация

Проведено моделирование методом молекулярной динамики процесса торможения заряженных частиц, движущихся в потном ультрахолодном замагниченном электронном газе. Рассмотрен случай однородного магнитного поля. Рассмотрено движение ионов с зарядом +е и –е. Исследована зависимость эффективности торможения от знака заряда, а также от угла между скоростью иона и направлением магнитного поля. Проведено сравнение результатов моделирования с имеющимися теоретическими моделями и ранее полученными результатами.

Ключевые слова: молекулярная динамика, столкновения в плазме, электронное охлаждение.

BRAKING EFFICIENCY OF POSITIVELY AND NEGATIVELY CHARGED PARTICLES IN ULTRA-COLD GAS OF MAGNETIZED ELECTRONS

Research article

Bobrov A.A. *

Joint Institute for High Temperatures of the Russian Academy of Sciences, Moscow, Russia

* Corresponding author (abobrov[at]inbox.ru)

Abstract

We performed the molecular dynamics simulation of the braking process of charged particles moving in a dense ultra-cold magnetized electron gas. The case of the uniform magnetic field is considered. The motion of ions with a charge +e and –e is considered. The dependence of the braking efficiency on the sign of the charge, as well as on the angle between the ion velocity and the direction of the magnetic field, is investigated. Results of the simulation are compared with available theoretical models, as well as with the previously obtained results.

Keywords: molecular dynamics, plasma collisions, electron cooling.

Введение

Интерес к задаче о торможении ионов в газе замагниченных электронов впервые возник в связи с идеей электронного охлаждения, впервые предложенной Будкером [1]. В рамках решения задачи о торможении Дербеневым и Скринским была предложена физическая модель [2], [3], позволяющая рассчитать эффективную силу трения, действующую на заряженную частицу.

В последнее время интерес к этой задаче усилился в связи с экспериментами по получению антиводорода [4]. В этих экспериментах для получения атомов антиматерии антипротоны инжектируются в облако замагниченных позитронов. Для описания процессов торможения антипротонов в позитронах также может применяться модель [2], [3].

В теоретических моделях, описывающих торможение ионов как в системе замагниченных частиц [2], [3], так и в обычных кулоновских системах [5] без магнитного поля, результирующие выражения для силы трения получаются симметричными относительно знаков зарядов, то есть содержат величины зарядов взаимодействующих частиц в четной степени. Однако появился ряд численных и экспериментальных результатов, показывающих, что сила трения, действующая на ион, распространяющийся в газе электронов, может зависеть не только от абсолютной величины, но и от знака заряда.

Экспериментальное отличие торможения положительно и отрицательно заряженных ионов в пучке замагниченных электронов было обнаружено в [6]. При этом более сильное трение испытывали отрицательные ионы. Отличия во взаимодействии ионов разного знака с электронным газом были получены в численных расчетах [7]. В этих расчетах решалась задача с изотропным распределением частиц по скоростям и в результате более сильное трение испытывали положительные ионы, в отличие от [6]. В [8] были также проделаны численные расчеты при условии изотропного распределения частиц по скоростям как в сильном магнитном поле, так и без магнитного поля, в результате, как и в [7] сила трения для положительных ионов оказалась больше, чем для отрицательных.

Целью настоящей работы является численное исследование методом молекулярной динамики процессов торможения положительно и отрицательно заряженных ионов в газе замагниченных электронов. Для того, чтобы снять противоречие расчетов [7] и [8] с экспериментальными результатами [6], в настоящей работе в отличие от [7] и [8] проведено исследование зависимости силы трения, действующей на ионы от угла между направлением скорости иона и магнитного поля.

Статья построена следующим образом: сначала приводится краткое описание теоретической модели Дербенева и Скринского, затем описывается метод расчета, в заключение приводятся результаты расчетов и обсуждение.

Модель Дербенева и Скринского

В модели Дербенева и Скринского [2], [3] сила трения, действующая на ион, движущийся в газе электронов, получается при пренебрежении поперечным движением электронов. То есть рассматривается случай такого сильного магнитного поля, что электроны имеют только одну степень свободу и могут двигаться только по оси, параллельной магнитному полю (то есть являются «замагниченными»). В рамках этой модели в приближении линейного отклика сила трения может быть записана в виде:

   (1)

где e – элементарный заряд, Z – зарядовое число иона, n – концентрация электронов, m – масса электрона,– скорость иона,  – модуль относительной скорости иона и скорости  «ларморовского кружка», представляющего электрон,  - компоненты скорости иона поперек и вдоль магнитного поля, . Кулоновский логарифм  в этом случае записывается в виде

где  - плазменная частота. Усреднение 〈...〉 производится по одномерному распределению электронов по скоростям (по компоненте скорости электронов, параллельной магнитному полю).

Метод расчета

Для моделирования процесса торможения ионов в газе замагниченных электронов применялся метод молекулярной динамики. Один ион с зарядом  или -1 и с массой, равной массе протона и 200 электронов помещались в кубическую ячейку моделирования.

Начальное распределение электронов по скоростям задавалось соответствующим температуре  K, начальное распределение по координатам задавалось случайным. Концентрация электронов задавалась равной  см^-3. Вдоль одного из ребер ячейки моделирования было направлено магнитное поле величиной 3 Тл. Эти параметры характерны для экспериментов [4].

Для частиц решались классические уравнения движения в рамках периодических граничных условий в микроканоническом ансамбле. Магнитная сила Лоренца, действующая на заряженные частицы, учитывалась по методу Бориса [9]. Использовался неизмененный кулоновский потенциал взаимодействия и метод с переменным шагом,  более подробное описание метода см. в [10].

В процессе моделирования скорость иона со временем уменьшалась. Зависимости компонентов квадрата скорости иона от времени аппроксимировались экспоненциальной функцией  – константа затухания.

Для исследования зависимости констант затухания от направления скорости иона, расчеты проводились для разных значений отношения квадрата компонент скорости иона , при фиксированной начальной скорости , где E  – кинетическая энергия иона, m_p – масса протона.

Результаты и обсуждение

Расчеты проведены для трех начальных энергий иона 7500, 15000 и 30000 К. Эти параметры соответствуют трем случаям: скорость иона меньше характерной тепловой скорости электронов для  К (для 7500 К), порядка тепловой скорости (для 15000 К) и больше тепловой скорости (для 30000 К). Для каждого значения энергии и отношения r проводилось 200 расчетов с разными начальными пространственными распределениями частиц. Затем временные зависимости усреднялись и аппроксимировались экспонентой.

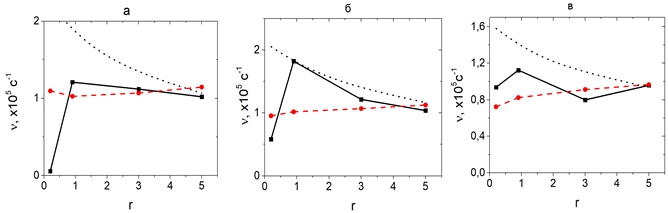
Рис. 1 – Константа затухания  для начальной энергии иона 7500 К (а), 15000 К (б) и 30000 К (в):

квадраты и сплошная линия – Z=+1, кружки и пунктир - Z=-1, короткий пунктир – формула (1)

 

На рисунке 1 представлены константы затухания для продольного направления. Расчетные значения представлены точками, соединенными отрезками. Также на рисунках нанесены теоретические кривые по формуле (1). Для определения теоретической константы затухания использовалось соотношение:

 

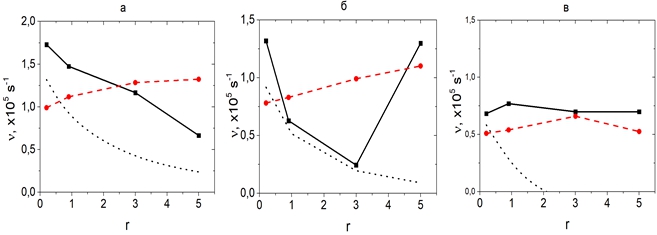
Рис. 2 – Константа затухания ; обозначения такие же, как на рисунке 1

 

На рисунке 2 представлены зависимости поперечной константы затухания для тех же значений энергии, что и на рисунке 1. Видно, что и в поперечном направлении торможение для отрицательных ионов может быть как больше, так и меньше, чем для положительных. Из рисунка видно, что формула (1) не описывает поведение силы трения в поперечном направлении даже качественно. Следует отметить, что в экспериментах поперечное затухание скорости как правило не измеряется, в частности в [6] есть данные только по продольному затуханию.

Заключение

В настоящей работе проведено моделирование процесса торможения положительно и отрицательно заряженных ионов в холодном газе замагниченных электронов. Показано, что в зависимости от угла между скоростью иона и направлением магнитного поля трение для положительных ионов может быть как больше, так и меньше, чем для отрицательных. Также отметим, что теоретическая модель [2], [3] в определенной области параметров не совпадает с полученным в расчетах затуханием ни для положительных ни для отрицательных ионов. В этой связи актуально развитие модели для описания ведущихся в настоящее время экспериментов по антиводороду [4].

Финансирование Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 18-32-00421.	Funding The reported study was funded by RFBR according to the research project № 18-32-00421.
Конфликт интересов Не указан	Conflict of Interest None declared

Список литературы / References

1. Budker G. I. Experimental studies of electron cooling / Budker G. I., Dikanskij N. S., Pestrikov D. V. et al. // Part. Accel. - 1976. – V. 7. – P. 197-211.
2. Derbenev Y. S. The effect of an accompanying magnetic field on electron cooling / Derbenev Y. S., Skrinsky A. N. // Part. Accel. – 1978. – V. 8. – P. 235-243.
3. Fedotov A. V. Numerical study of the magnetized friction force / Fedotov A. V., Bruhwiler D. L., Sidorin A. O. et al. // Physical Review Special Topics-Accelerators and Beams. – 2006. - V. 9. - №7. – P. 074401.
4. Amoretti M. High rate production of antihydrogen / Amoretti M. // Physics Letters B. – 2004. – V. 578. - №1-2. P. 23-32.
5. Spitzer L. Physics of Fully Ionized Gases / Spitzer L. - New York: Wiley, 1962.
6. Dikanskii N. S. Influence of the sign of the charge of an ion on the friction force in electron cooling / Dikanskii N. S., Kot N. K., Kudelainen V. I. t al. // JETP. – 1988. - V. 67. - №1. - P. 35
7. Ordonez C. A. Possibilities for achieving antihydrogen recombination and trapping using a nested Penning trap and a magnetic well / Ordonez C. A., Dolliver D. D., Chang Y. // Physics of Plasmas. - 2002. – V. 9. - №8. - P. 3289-3302.
8. Bobrov A. A. Proton energy relaxation in an electron gas in a uniform magnetic field. Plasma Physics Reports / Bobrov A. A., Bronin S. Y., Zelener B. B. et al. – 2017. – V. 43. - №5. – P. 547-554.
9. Birdsall C. K. Plasma Physics via Computer Simulation / Birdsall C. K., Langdon A. B. –New York : McGraw-Hill, 1985.
10. Bobrov A. A. Energy relaxation rate in antiproton–positron nonneutral plasma / Bobrov A. A., Bronin S. Y., Zelener B. B. et al. // Journal of Physics: Conf. Series. – 2018. – V. 946. – P. 012129