МОДЕЛИРОВАНИЕ ДВИЖЕНИЯ ШАРОВ В ПЛАНЕТАРНОЙ МЕЛЬНИЦЕ С ПОМОЩЬЮ SOLIDWORKS

МОДЕЛИРОВАНИЕ ДВИЖЕНИЯ ШАРОВ В ПЛАНЕТАРНОЙ МЕЛЬНИЦЕ С ПОМОЩЬЮ SOLIDWORKS

Научная статья

Чайка В.А.^1, *, Савин В.В.², Савина Л.А.³, Осадчий А.В.⁴, Мелешко А.В.⁵

¹ ORCID: 0000-0003-3877-2383;

² ORCID: 0000-0002-7166-4133;

³ ORCID: 0000-0002-8181-5169,

^{1, 2, 3} Балтийский федеральный университет им. Иммануила Канта, Калининград, Россия;

⁴ ORCID: 0000-0002-6882-9953,

⁴ Институт общей физики им. Прохорова РАН, Москва, Россия;

⁵ ORCID: 0000-0003-0377-6165,

⁵ Запорожский авиационный колледж, Запорожье, Украина

* Корреспондирующий автор (v_chayka8[at]rambler.ru)

Аннотация

Для понимания термодинамического аспекта процессов при механоактивационной обработке оцениваются энерговыделения в мельницах различного типа. Моделирование движения шаров мельницы и оценка генерации энергии в системе шаров трудоемкая задача, зачастую описываемая системой более десятка уравнений. Компьютеризация решения такой задачи требует порой специализированных программ и больших компьютерных мощностей. В работе показано как с помощью программного комплекса Solidworks можно выполнить моделирование движения шаров в планетарной мельнице. По результатам моделирования определен оптимальный состав размеров шаров и оценено энерговыделение в системе шаров.

Ключевые слова: моделирование движения шаров, планетарная мельница.

SIMULATION OF THE MOTION OF BALLS IN A PLANETARY MILL USING SOLIDWORKS

Research article

Chaika V.A.^1, *, Savin V.V.², Savina L.A.³, Osadchy A.V.⁴, Meleshko A.V.⁵

¹ ORCID: 0000-0003-3877-2383;

² ORCID: 0000-0002-7166-4133;

³ ORCID: 0000-0002-8181-5169,

^{1, 2, 3} Immanuel Kant Baltic Federal University, Kaliningrad, Russia;

⁴ ORCID: 0000-0002-6882-9953,

⁴ Prokhorov General Physics Institute of the Russian Academy of Sciences, Moscow, Russia;

⁵ ORCID: 0000-0003-0377-6165,

⁵ Zaporizhia Aviation College, Zaporozhe, Ukraine

* Corresponding author (v_chayka8[at]rambler.ru)

Abstract

To understand the thermodynamic aspect of processes during mechanoactivation processing, the energy release in mills of various types is estimated. Simulation of the motion of balls of a mill and estimating the generation of energy in a system of balls is a time-consuming task, often described by a system of more than a dozen equations. The computerization of solving such a task sometimes requires specialized programs and large computer capacities. The paper shows how using the Solidworks software package you can simulate the movement of balls in a planetary mill. According to the simulation results, the optimal composition of ball sizes was determined and the energy release in the system of balls was estimated.

Keywords: ball motion simulation, planetary mill. Introduction

Nowadays, industry widely uses mills of various types and not only for crushing, grinding, but also in the modern rapidly developing direction of mechanical alloying (fusion, synthesis), the so-called mechanical activation processing in order to obtain composite nanomaterials and alloys in the amorphous state [1], [2]. To increase the efficiency and expand the capabilities of the considered method (technology) of material processing, it is necessary to be able to predict (calculate, evaluate or simulate) the characteristics of the impact of the mechanical activation system with the material processed in it, including the interaction of the processed particles with each other. Therefore, today many researchers are engaged in modeling the movement of grinding bodies in the mill in order to quantify the energy introduced into the processed material during mechanical activation processing. The physical and mathematical description of the motion of grinding bodies contains a large number of complex equations, including a matrix type, whose solution requires the use of tensor analysis methods and cumbersome computational calculations. As a result, carrying out such calculations and interpreting the obtained results require large computer capacities, considerable time and a complex algorithm for their visualization (modeling the process under consideration).

In this paper, we propose a simplified approach to modeling the process of mechanical activation of the powder material in ball planetary mills of the type PM100 (manufacturer, Retsch, Germany [10]), which does not require complex implementation. The aim of the work is to simulate the movement of balls in a planetary mill using the Solidworks software, determine the optimal number and ratio of ball sizes for a fixed cup size and quantify the average energy released in the ball system during mechanical activation processing.

Results

To quantify the average energy transferred to the material by the balls interacting with each other and the powders during the mechanical activation treatment in a planetary mill, we simulated the motion of balls in the volume of a cylindrical cup of the Retsch PM 100 ball mill used in our work. In the mill, the glasses with the grinding bodies rotate around their own axis, which rotates around the axis of the mill. The speed of the planetary mill varies from 100 to 650 rpm. The simulation was performed in the Solidworks software package using the procedure of fixing the averaged values for one ball: the translational and angular velocity of the balls, their translational and angular acceleration, energy and force of action on the glass walls by all the balls. The time for modeling the motion of the balls was 1 sec, since the values of all fixed parameters during this time stabilized around a certain value. Since the program does not have the capacity to introduce a large number of objects, the modeling was carried out in stages with a step-by-step increase in the number of objects.

At the first stage, 12 balls with a diameter of 10 mm were placed in a single layer in a glass with r = 3.25 cm and a height of 6 cm. The radius of the carrier of the glass was R = 7 cm, the rotation of the carrier and the glass was W = w = 600 rpm. The glass and the carrier rotate in one direction clockwise. The density of the material of the glass and balls 7.8 g/cm³.

Since in reality the balls move not only along the bottom of the glass, but also throughout its volume, it was decided to group the balls into 4 pieces. into tetrahedra. This assumption is legitimate, since at any given moment in time all the balls can be divided into groups (into tetrahedra), which have the same error (the agreed speed and acceleration) with an allowable fraction of the error. This made it possible to introduce into the calculation system a large number of objects, gradually approaching the real state of the system when the glass is filled with balls by two thirds of the volume.

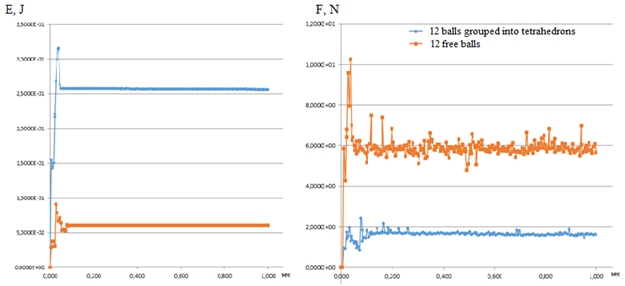
Comparing the obtained values of the motion parameters of grouped and non-grouped balls, it can be concluded that the distribution of balls in the volume, compared with the plane distribution of balls on the bottom of the glass, gives an increased average value of the energy of the balls and their force on the walls of the glass (Fig. 1). When calculating the average energy, it is necessary to take into account that for balls grouped into a tetrahedron, the value of this parameter is divided into four.

Fig. 1 – The energy of the ball and the force of the impact of the ball on the glass

 

The following modeling steps were performed: modeling the motion of balls in the amount of 12, 16, 20, 24, 28, and 32 balls, which are grouped into tetrahedra. Fragments of a typical movement are shown in Fig.2.

Fig. 2 – Fragments of motion of 32 balls grouped into tetrahedrons

 

By analyzing changes in the values of parameters and performing approximations, one can obtain the parameters of the optimal mode. When the system moves to a larger number of tetrahedra, the force values for one tetrahedron vary from 5.9 to 6.9 N, and energies from 0.26 to 0.24 J. Accordingly, as the number of tetrahedra increases, the total energy values increase.

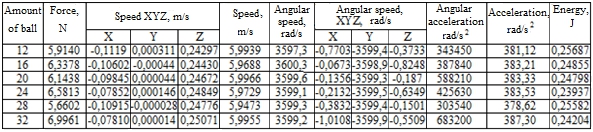
Since the material was being processed is affected not only by the surface of the glass, but also throughout the entire volume, changes in parameters such as the speed and acceleration of the ball are analyzed (see Table 1). The following graphs are constructed according to the parameter modules without direction. Table 1 presents the parameter values for a single 10 mm ball, which is located in a system with a different number of balls. The axis OY coincides with the axis of the glass.

 

Table 1 – The results of simulation of movement in the system of 10 mm balls (average steady-state values without direction)

Note: the simulation was carried out in the Solidswork computer complex, in which the values provided are the result of averaging over the time period of each analysis act. For 10 mm balls, this period was 0.005 s

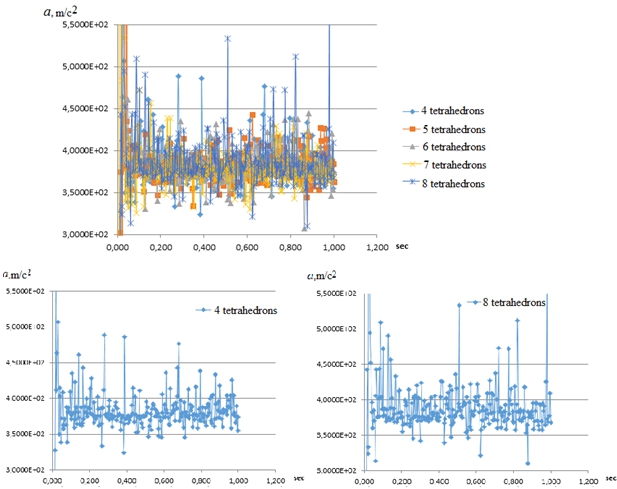
Analyzing the graphs of the acceleration, we can assume that the system approaches the state of resonance with 4 tetrahedrons and 8 tetrahedrons (16 and 32 balls, respectively), as evidenced by strong bursts in the corresponding graphs of translational acceleration (Fig. 3).

Fig. 3 – Forward acceleration for the ball system

 

When analyzing the angular acceleration, strong bursts of values are detected for systems with 6, 7, and 8 tetrahedrons (Fig. 4).

It is noteworthy that the angular acceleration and the force of action of the ball on the surface of the glass takes on maximum values for a system of 8 tetrahedrons.

Since the aim of the project in which this work is being implemented is to obtain the most dispersed powder material, based on the principle of achieving maximum packing density of spherical bodies, it was proposed to use a set of balls of different diameters. Therefore, the next stage of modeling was the study of the effect of introducing balls of the second diameter into the mechanoactivation

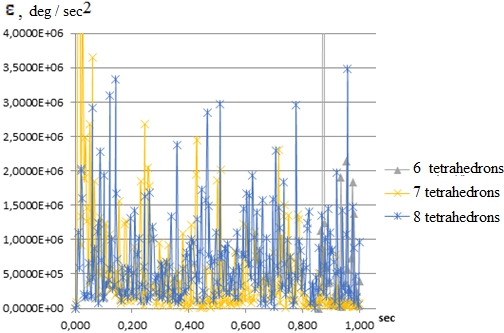
Fig. 4 – Angular acceleration bursts for systems of 6, 7, and 8 tetrahedrons system of balls

 

The diameter and the number of balls of the second size were chosen to be multiples of the size and number of octa-or / and tetra-pores in the structure of close-packed balls of the original size. Since the state of the system for 7 and 8 tetrahedrons approaches the resonant one, it was decided to use 5 groups of 5 balls of 10 mm each (ie, one ball was added to the tetrahedron), to which 6 pieces of balls with a diameter of 15 5 and 2 mm were added. Table 2 presents the parameter values for one group of 10 mm balls in the system of balls with the addition of 15; 5 and 2 mm balls. For a system of balls with 5 and 2 mm balls, the values for one group of 10 mm balls are almost the same.

 

Table 2 – Parameter values for a group of 10 mm balls in the ball system (average steady-state values without direction)

Table 3 presents the parameter values for a single ball with a diameter of 15; 5 and 2 mm.  

Table 3 – Parameters for one ball in a system of balls of different diameters (average steady-state values without taking into account the direction)

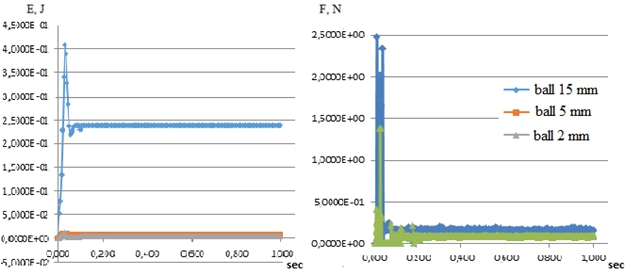
The effect of balls 5 and 2 mm on the inner surface of the glass and their energy practically have similar values that differ from those for balls 15 mm (see Fig. 5).

Fig. 5 – The energy of one ball and the force of impact of one ball on the inner surface of the glass

 

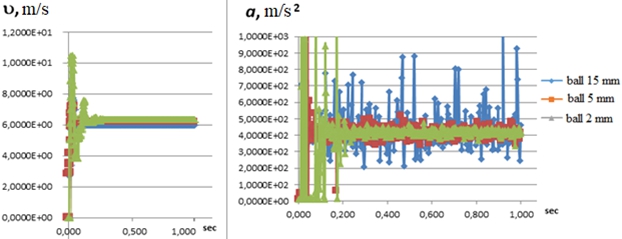
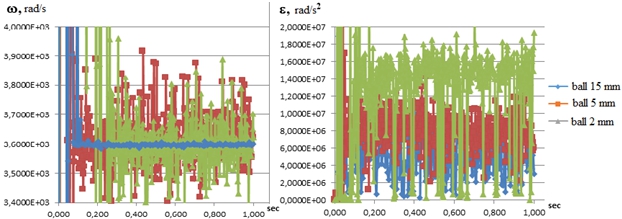
The forward speed and acceleration of balls of 15, 5, and 2 mm differ little (Fig. 6). The angular velocity of the 15 mm ball does not have strong bursts, in contrast to 5 and 2 mm balls (Fig. 7). And the angular acceleration of a 2 mm ball is almost an order of magnitude larger than the other balls (Fig. 7).

Fig. 6 – Forward speed and progressive acceleration of one ball

Fig. 7 – Angular velocity and angular acceleration of one ball

 

According to the results of modeling the movement of balls in the mill, we estimate the energy received by the glass as the balls move according to the formula:

Е_gl = t*(F_gr *t_gr *u_гр*5 + F_b15 *t_b15*u_b15*13 + F_b5 *t_b5 *u_b5*8 + F_b2 *t_b2 *u_b5*5),

where F is the force of impact on the inner surface of the glass during the exposure time t, respectively: gr - groups of balls 10 mm, b15 - ball 15 mm, b5 - ball 5 mm and b2 - ball 2 mm.

Е_gl = 60*60s*(13,2N/s*0,005s*5,89 m/s*5 + 10N/s*0,005s*5,97m/s*13+ +0,17N/s*0,003s*6,19m/s*8+ 0,08N/s*0,003s*6,36m/s*5) *3600s = (1,9437J/s+ +3,8805J/s +0,0253J/s+0,007632J/s) *3600s = 5,857*3600 J = 21085,68 J

Discussion

Since in the volume of the glass the collision energy between the balls is also released, the total energy released will be 1.5 times more Eats. The resulting value of energy E_t ~ 31.6 kJ is greater than the calculated energy introduced into the material: E = 27.7 kJ. The difference in values can be attributed to the thermal phenomena present during processing in the mill.

Conclusion

The paper shows that when combining balls into small groups, you can simulate the movement of a set of balls of different diameters in a planetary mill using the Solidworks software.

According to the simulation results, the optimal composition of ball sizes was determined and the energy release in the system of balls was estimated.

Финансирование Исследование было поддержано из средств субсидии, выделенной на реализацию Программы повышения конкурентоспособности БФУ им. И. Канта. Работа выполнены по проекту №16.1419.2017/ПЧ, финансируемого Министерством образования и науки Российской Федерации.	Funding The study was supported by a subsidy allocated for the implementation of the Program for Enhancing the Competitiveness of the Immanuel Kant Baltic Federal University. The work was performed under the project No. 16.1419.2017/PCh, financed by the Ministry of Education and Science of the Russian Federation.
Конфликт интересов Не указан.	Conflict of Interest None declared.

Список литературы / References

1. Suryanarayana c. mechanical alloying and milling. Progress in materials science, 2001, vol. 46, pp. 1-184.
2. Savin, V.V. Formation of amorphous powders of alloys of cu-ti system with mechanical activation of powder mixtures (1998) powder metallurgy and metal ceramics  / Savin, V.V., Chayka, V.A, 37 (7-8), pp. 448-451
3. Шелехов Е.В. Компьютерное моделирование процесса механического сплавления в шаровых мельницах / Шелехов Е.В., Свиридова Т.А. // Материаловедение. – 2007. – № 11. – с. 13–21.
4. Шелехов Е.В. Компьютерное моделирование процесса механического сплавления в шаровых мельницах / Шелехов Е.В., Свиридова Т.А.  // Материаловедение. – 2007. – № 12. – с. 10–15.
5. Шелехов Е.В. Компьютерное моделирование процесса механического сплавления в шаровых мельницах. ч. iii. Кинетика движения мелющих тел и расчет температуры мелющей среды / Шелехов Е.В., Свиридова Т.А. // Материаловедение. – 2008. – № 2. – с. 10–22.
6. Шелехов Е.В. Компьютерное моделирование процесса механического сплавления в шаровых мельницах. ч. iii. Кинетика движения мелющих тел и расчет температуры мелющей среды (окончание iii ч.) / Шелехов Е.В., Свиридова Т.А. // Материаловедение. – 2008. – № 3. – с. 11–25.
7. Кузьмич Ю.В. Модель энергетических характеристик планетарной мельницы / Кузьмич Ю.В., Коротков В.Г. //Труды Кольского научного центра РАН.- 2015.- № 1.- С. 380–384.
8. Зубко И.Ю. Моделирование движения мелющих тел в процессе механического легирования / Зубко И.Ю., Зайцев А.В. // Вестник ПНИПУ. Аэрокосмическая техника. № 48. С. 5-15. doi: 10.15593/2224-9982/2017.48.01.
9. Feng Y.T. Discrete element simulation of the dynamics of high energy planetary ball milling processes. Materials Science and Engineering A / Feng Y.T., Han K., Owen D.R.J., 2004, vol. 375-377, pp. 815-819.
10. https://www.retsch.ru/ru/products/milling/ball-mills/planetary-ball-mill-pm-100-cm/function-features.

Список литературы на английском языке / References in English

1. Suryanarayana C. Mechanical alloying and milling. Progress in Materials Science, 2001, vol. 46, pp. 1-184.
2. Savin, V.V. Formation of amorphous powders of alloys of Cu-Ti system with mechanical activation of powder mixtures (1998) Powder Metallurgy and Metal Ceramics / Savin, V.V., Chayka, V.A., 37 (7-8), pp. 448-451.
3. Shelehov E.V. Kompyuternoe modelirovanie protsessa mekhanicheskogo splavleniya v sharovykh melnitsakh [Simulation of mechanical alloying in ball mills] / Shelehov E.V., Sviridova T.A. Materialovedenie, 2007, № 11, pp. 13-21.
4. Shelehov E.V. Kompyuternoe modelirovanie protsessa mekhanicheskogo splavleniya v sharovykh melnitsakh [Simulation of mechanical alloying in ball mills] / Shelehov E.V., Sviridova T.A. Materialovedenie, 2007, № 12, pp. 10-15.
5. Shelehov E.V. Kompyuternoe modelirovanie protsessa mekhanicheskogo splavleniya v sharovykh melnitsakh. Chast III. Kinetika dvizheniya melyushchikh tel i raschet temperatury melyushchey sredy [Simulation of mechanical alloying in ball mills. Part III. Kinetics of milling bodies motion and computation of milling mass temperature]. / Shelehov E.V., Sviridova T.A. Materialovedenie, 2008, № 2, pp. 10-22.
6. Shelehov E.V. Kompyuternoe modelirovanie protsessa mekhanicheskogo splavleniya v sharovykh melnitsakh. Chast III. Kinetika dvizheniya melyushchikh tel i raschet temperatury melyushchey sredy (okonchanie III ch.) [Simulation of mechanical alloying in ball mills. Part III. Kinetics of milling bodies motion and computation of milling mass temperature (continuation of part III)] / Shelehov E.V., Sviridova T.A.. Materialovedenie, 2008, № 3, pp. 11-25.
7. Kuzmich Yu.V. Model' energeticheskikh kharakteristik planetarnoy mel'nitsy [Simulation of the energy characteristics of the planetary mill]/ Kuzmich Yu.V., Korotkov V. G. // Trudy Kol'skogo nauchnogo tsentra RAN [Proceedings of the Kola Scientific Center of the Russian Academy of Sciences].- 2015.- №- P. 380–384. [in Russian]
8. Zubko I.Yu. Modelirovaniye dvizheniya melyushchikh tel v protsesse mekhanicheskogo legirovaniya [Simulation of milling balls motion within mechanical alloying process] / Zubko I.Yu., Zaitsev A.V. // Vestnik PNIPU. Aerokosmicheskaya tekhnika [Bulletin PNRPU. Aerospace engineering]. 2017. № 48. P. 5-15. doi: 10.15593 / 2224-9982 / 2017.48.01.[in Russian]
9. Feng Y.T. Discrete element simulation of the dynamics of high energy planetary ball milling processes. Materials Science and Engineering A, 2004, vol. 375-377, pp. 815-819.
10. https://www.retsch.ru/ru/products/milling/ball-mills/planetary-ball-mill-pm-100-cm/function-features