МОДЕЛЬНЫЕ ХАРАКТЕРИСТИКИ МАГНИТНЫХ СИСТЕМ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ И ИЗУЧАЕМЫХ ОБРАЗЦОВ

МОДЕЛЬНЫЕ ХАРАКТЕРИСТИКИ МАГНИТНЫХ СИСТЕМ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ И ИЗУЧАЕМЫХ ОБРАЗЦОВ

Научная статья

Ткаченко Р.Ю.¹, Мишина Е.Д.², Сандуляк А.В.³, Полисмакова М.Н.⁴, Сандуляк А.А.^5, *, Сандуляк Д.А.⁶

¹ ORCID: 0000-0002-6951-059Х;

³ ORCID: 0000-0001-7605-2702;

⁴ ORCID: 0000-0002-4564-6206;

⁵ ORCID: 0000-0002-5111-6092;

^{1, 2, 3, 4, 5, 6} МИРЭА – Российский технологический университет, Москва, Россия

* Корреспондирующий автор (m.polismakova[at]mail.ru)

Аннотация

Выполнено компьютерное моделирование (в программной среде COMSOL Multiphysics 5.3) магнитных систем измерительных устройств типа «многосекционный удлиненный соленоид с изучаемым образцом», «магнетометр Фарадея (полюсные наконечники сферической формы)» для оперативного получения прогнозных магнитных характеристик этих систем и изучаемых в них образцов. Приведены модельные полевые зависимости индукции поля в сплошных и гранулированных (засыпка шаров) образцах цилиндрической формы – при различных отношениях длины образца к его диаметру, показано их отличие от соответствующих предельных (получаемых экспериментально для достаточно «длинных» образцов) зависимостей. Приведены также модельные координатные характеристики индукции поля в межполюсной области магнетометра – при различных значениях расстояния между полюсами и токовой нагрузки; выявленный их извилистый тренд (с перегибом) указывает на наличие требуемых (для размещения исследуемого образца) зон стабильности градиента.

Ключевые слова: компьютерное моделирование, магнитные системы измерительных устройств, сплошной и гранулированный образцы, полевые и координатные зависимости индукции. 

MODEL CHARACTERISTICS OF MAGNETIC SYSTEMS OF MEASURING DEVICES AND STUDIED SAMPLES

Research article

Tkachenko R.Yu.¹, Mishina E.D.², Sandulyak A.V.³, Polismakova M.N.⁴, Sandulyak A.A.^5, *, Sandulyak D.A.⁶

¹ ORCID: 0000-0002-6951-059Х;

³ ORCID: 0000-0001-7605-2702;

⁴ ORCID: 0000-0002-4564-6206;

⁵ ORCID: 0000-0002-5111-6092;

^{1, 2, 3, 4, 5, 6} MIREA – Russian Russian Technological University, Moscow, Russia

* Corresponding author (m.polismakova[at]mail.ru)

Abstract

The authors conducted computer simulations (in the COMSOL Multiphysics 5.3 software environment) of magnetic systems of measuring devices such as “multi-section elongated solenoid with a test sample,” “Faraday magnetometer (pole tips of spherical shape)” to obtain predictive magnetic characteristics of these systems and the samples studied in them. Model field dependences of field induction in solid and granular (filling balls) cylindrical specimens are given for various ratios of the sample length to its diameter, and they are shown to differ from the corresponding limit (experimentally obtained for fairly “long” samples) dependencies. Model coordinate characteristics of the field induction in the interpolar region of the magnetometer are also given for various values of the distance between the poles and the current load; their twisty trend (with an inflection) revealed the presence of gradient stability zones required for placing the sample under study.

Keywords: computer simulation, magnetic systems of measuring devices, solid and granular samples, field and coordinate dependences of induction.

При решении многих технико-технологических задач, связанных с применением магнитного поля в реализации производственных процессов, необходимо располагать данными о магнитных свойствах элементов и узлов оборудования, обеспечивающего создание этого поля, а также данными о магнитных свойствах дисперсных фаз рабочих сред, подвергаемых воздействию магнитного поля.

В частности, такая необходимость всегда возникает в случае предполагаемого применения магнитных сепараторов, предназначенных для выделения из жидких, сыпучих и газообразных сред ферро- и ферримагнитных включений (полезных или примесных): в горнодобывающей, энергетической, химической, металлургической и других отраслях промышленности. Так, для создания высокоградиентных магнитных сепараторов фильтрационного типа, в которых магнитное воздействие на среду осуществляется в матрице, представляющей собой «упаковку» ферромагнитных тел, например, засыпку шаров, крайне необходимой является информация о магнитных свойствах этих матриц. И в такой информации речь должна идти о практически используемых, геометрически разных, образцах матриц (на примере цилиндрических образцов – при различных значениях отношения длины образца L к его диаметру D). Кроме того, для создания магнитных сепараторов, особенно когда стоит задача строго адресного их применения, столь же необходимой является и информация, касающаяся магнитных свойств выделяемых феррочастиц, о которых можно судить по магнитным свойствам дисперсных образцов таких частиц.

Все это требует выполнения магнитных измерений с привлечением для этого соответствующих методов измерения и устройств для их реализации (содержащих те или иные магнитные системы). Так, для получения информации о магнитных свойствах образцов гранулированных матриц (как и обычных сплошных образцов, например, из стали) можно использовать баллистический метод, практичный вариант которого реализуется с применением достаточно длинного, а потому секционного, соленоида. Для получения же информации о магнитных свойствах дисперсных образцов феррочастиц, выделяемых из среды, подлежащей магнитной сепарации, целесообразно использование высокочувствительного пондеромоторного метода – с помощью магнетометра Фарадея: ввиду получения, как правило, объективно малых по объему образцов, что недостаточно для реализации того же баллистического метода. При этом предпочтительно применять в таком магнетометре полюса сферической формы, что дает возможность создания и обнаружения зон стабильности градиента и магнитного силового фактора – для размещения изучаемого образца [5], [6], [7].

Надо сказать, что получение необходимой информации о магнитных свойствах образцов матриц и дисперсных (с дисперсной фазой феррочастиц) образцов требует выполнения большого объема экспериментов. Следовательно, такой, сугубо экспериментальный, подход, хотя и гарантирует наиболее достоверные результаты, является затратным, трудоемким и, что особенно нежелательно в условиях безотлагательного принятия тех или иных решений – сравнительно долгосрочным.

Вместе с тем, эта информация может последовать, причем намного более оперативно, из соответствующего компьютерного моделирования (методом конечных элементов) той или иной магнитной измерительной системы и характерных особенностей ее функционирования. При этом, разумеется, проверка на соответствие модельных, во многих случаях – как прогнозных, данных и экспериментальных данных остается вполне правомочной и необходимой.

Система: многосекционный (удлиненный) соленоид с изучаемым образцом

Как указано выше, при решении многих научных и практических задач существует потребность в информации о магнитных свойствах образцов разных размеров. Для оценки соответствующей роли этих размеров целесообразно получить полевые зависимости индукции поля B в обычно изучаемых (в таких и подобных случаях) образцах цилиндрической формы – при разных значениях отношения длины образца L к его диаметру D, т.е. разных значениях L/D.

Для оперативного получения (путем моделирования) таких зависимостей, полезных при прогнозной оценке роли параметра L/D, необходимо располагать экспериментальной зависимостью B от H, присущей именно материалу данного образца. Такую зависимость, т.е. кривую намагничивания, можно найти экспериментально, используя, как известно, тороидальный или достаточно длинный цилиндрический образец (L/D ≥ 50 для сплошного стального образца [8] и L/D ≥ 10-12 для гранулированного образца в виде засыпки подшипниковых шаров [9]), когда размагничивающий фактор образца либо отсутствует вообще, либо сведен к минимуму. В случае использования цилиндрического образца его можно помещать в соленоид.

Параметры предназначенного для этого шестисекционного многослойного соленоида таковы: общая длина 778 мм, внутренний и внешний диаметры каждой из его секций 47,5 мм и 132 мм при длине 123 мм и числе витков 750. При этом зазоры между секциями, включая толщину неферромагнитных щек каркасов для катушек-секций, составляли 9,2 мм, за исключением зазора между двумя центральными секциями (3,5 мм). Величина тока питания секций – варьируемая: от I = 0,8 А до I = 8,3 А.

При осуществлении моделирования – методом конечных элементов в программной среде COMSOL Multiphysics 5.3, с количеством элементов здесь порядка 6∙10⁵ – размеры окружающей данную магнитную систему области, а именно куб с длиной ребра 2 м, следуя рекомендации [10], существенно превышали собственные размеры самой системы, габариты которой: 0,13х0,13х0,8 м.

Соответствующие результаты моделирования показали, что в отсутствие образца на концевых участках соленоида напряженность H создаваемого им магнитного поля, как известно, все более убывает. При длине каждого из этих концевых участков до 0,06 м их совокупная длина достигает примерно 0,12 м, что составляет 15 % всей длины соленоида. Следовательно, рабочим для размещения изучаемого образца может быть лишь «срединный», сравнительно протяженный, участок соленоида: начинающийся на расстоянии 0,06 м от одного торца соленоида и заканчивающийся соответственно на таком же расстоянии от другого его торца. Здесь длина этого рабочего участка соленоида: 0,658 м, напомним, при его общей длине 0,778 м.

Данные индукции поля B в используемом, достаточно длинном, образце в зависимости от напряженности создаваемого соленоидом поля H получали посредством измерения микровеберметром магнитного потока сквозь петлю, установленную в средней части образца (рис.1), с последующим делением величины этого потока на произведение сечения одного витка петли и числа витков.

На рис.2 (кривая E) показана экспериментальная полевая зависимость индукции, полученная для этого, достаточно «длинного», цилиндрического стального образца: длиной L = 600 мм и диаметром D = 12 мм, т.е. при L/D = 50 (заметим, что сталь образца соответствовала стали магнитопровода рассматриваемой ниже такой магнитной измерительной системы как магнетометр Фарадея). Значит, эта зависимость, полученная, напомним – для образца, относительная длина которого удовлетворяет критерию [8], практически в полной мере эквивалентна полевой зависимости индукции для самого материала такого рода сплошного образца.

На рис.3 (кривая E) показана экспериментальная полевая зависимость индукции, полученная для специфичного цилиндрического образца – гранулированного (засыпка шаров диаметром 8 мм из стали 95Х18 в корпусе диаметром D = 40 мм). Высота такого образца составляла L = 640 мм, т.е. L/D = 16. Значит, применительно к гранулированным средам – это тоже достаточно «длинный» образец [9] и получаемая для него полевая зависимость индукции практически в полной мере эквивалентна полевой зависимости индукции для «квазисплошного материала» такого рода образца.

Представленные на рис.2 (кривая E) и рис.3 (кривая E) экспериментальные полевые зависимости индукции в соответствующих «длинных» образцах, т.е. сплошном стальном – при L/D = 50 и гранулированном в виде засыпки шаров – при L/D = 16, являются необходимой информацией для моделирования полевых зависимостей «коротких» сплошных образцов (когда L/D < 50) и «коротких» гранулированных образцов (когда L/D < 13-16).

На рис.2 кривыми 1-10 и на рис.3 кривыми 1-9 показаны эти модельные полевые зависимости магнитной индукции как в сплошном, так и в гранулированном образцах при различных значениях L/D.

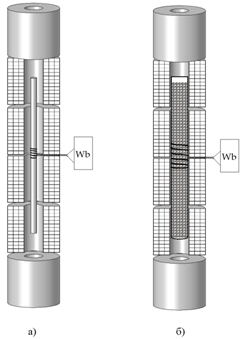
Рис. 1 – Реализация баллистического метода получения полевой зависимости индукции в сплошном (а) и гранулированном (б) образцах с применением шестисекционного многослойного соленоида

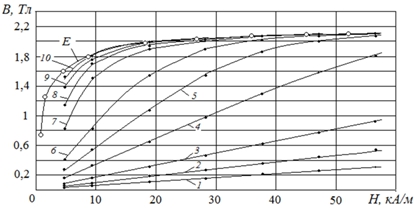
Рис. 2 – Модельные (1-10) полевые зависимости индукции в сплошных «коротких» образцах – с различными значениями L/D: 1 – L/D = 1; 2 – L/D = 1,8; 3 – L/D = 3; 4 – L/D = 5,5; 5 – L/D = 8; 6 – L/D = 11; 7 – L/D = 19; 8 – L/D = 25; 9 – L/D = 32; 10 – L/D = 43; кривая Е – экспериментальная зависимость для сплошного, достаточно «длинного», образца: L/D = 50

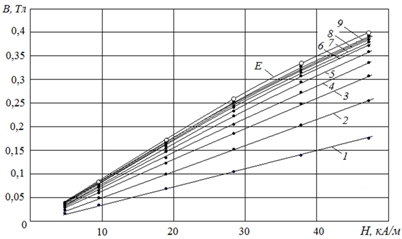
Рис. 3 – Модельные (1-9) полевые зависимости индукции в гранулированных «коротких» образцах – с различными значениями L/D: 1 – L/D = 1,01; 2 – L/D = 2,04; 3 – L/D = 3,12; 4 – L/D = 4,11; 5 – L/D = 5,43; 6 – L/D = 6,78; 7 – L/D = 8,27; 8 – L/D = 9,4; 9 – L/D = 12,9; кривая Е – экспериментальная зависимость для гранулированного (засыпка шаров), достаточно длинного, образца:  L/D = 16

 

Что касается сплошных образцов (рис.2), то отчетливо видно: полевые зависимости индукции 1-10 с уменьшением относительного габарита образца L/D располагаются все ниже, свидетельствуя тем самым об ухудшении их магнитных свойств. Нелишне при этом сравнить данные индукции из модельных зависимостей 1-10 с данными индукции из экспериментальной, т.е. предельной, зависимости E. Это сравнение дает основание судить о том, что по своим магнитным свойствам «короткие» образцы уступают «длинному» образцу, т.е. самому материалу этих образцов (с потенциально возможными магнитными свойствами), причем для малых значений L/D – весьма существенно. Например, для образца с сопоставимыми значениями длины и диаметра (L/D =1) значение индукции в нем более чем на порядок ниже, чем в «длинном» образце.

Что же касается гранулированных образцов (рис.3), то качественно полученные результаты остаются аналогичными предыдущим – как при сравнении модельных полевых зависимостей индукции 1-9 между собой, так и с экспериментальной, т.е. предельной, полевой зависимостью индукции E. Количественно же эти результаты несколько иные. Например, для такого же равновеликого (L/D =1), но гранулированного, образца значение индукции в нем по сравнению со значением индукции в «длинном» образце – примерно в два раза ниже, а не на порядок, как для уже упомянутого равновеликого сплошного образца.

Система: магнетометр Фарадея (полюсные наконечники сферической формы)

На рис.4 показан схематично усовершенствованный магнетометр Фарадея [5], [6], [7] применительно к которому тоже можно осуществить моделирование – с получением прогнозных характеристик создаваемого им неоднородного магнитного поля в межполюсной области.

В [5], [6], [7] описаны особенности этого магнетометра (рис.4), предназначенного, как и другие магнетометры такого же назначения, для измерения пондеромоторной силы, действующей на изучаемый образец (малого объема, в частности, порошка примесей-феррочастиц, выделенных из рабочей среды), и последующего определения магнитной восприимчивости образца. По сравнению с магнетометрами-аналогами он обладает существенным преимуществом: благодаря рекомендуемому в [5], [6], [7] применению полюсных наконечников в виде полусфер координатная характеристика индукции (напряженности) поля в межполюсной области должна иметь выраженный извилистый характер, т.е. иметь перегиб. Тем самым, в таком магнетометре можно, в отличие от ряда других магнетометров-аналогов, гарантированно создавать (и, что весьма важно – экспериментально и аналитически идентифицировать) зону стабильной неоднородности, т.е. зону позиционирования изучаемого образца: в окрестности перегиба координатной зависимости индукции и соответственно в окрестности экстремума координатной зависимости ее градиента [5], [6], [7].

 

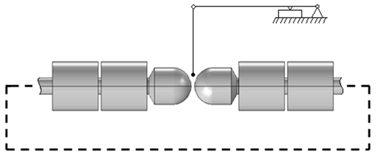
Рис. 4 – Схема магнетометра Фарадея – модернизированного [5], [6], [7] с применением полюсных наконечников сферической формы

 

Блок, представляющий первостепенный интерес для моделирования, отвечающий за создание в магнетометре градиентного магнитного поля (рис.4), состоит из четырех (двух сдвоенных) катушек намагничивания, замкнутого стального магнитопровода, имеющего полюсные наконечники с торцевой поверхностью сферической формы. Каждая катушка намагничивания, в которой внутренний и внешний диаметры составляют соответственно 47,5 мм и 132 мм, а длина – 123 мм, имеет 750 витков медного провода, зазоры между сдвоенными катушками, включая толщину щек каркасов, – до 8 мм. Величина тока питания катушек I – варьируемая в пределах от I = 1 А до I = 7,5 А. Габаритные размеры замкнутого стального магнитопровода (в виде прямоугольника) составляют 1240х300 мм, его диаметр в поперечном сечении за пределами полюсных наконечников – 50 мм, диаметр полюсного наконечника – 100 мм, его длина, включая конусный переход 100х50 мм длиной 15 мм, – 115 мм; имеются также (учитываемые при моделировании) зазоры в стыках элементов магнитопровода и детали крепежа. Расстояние между полюсными наконечниками b – варьируемое в пределах от b = 3,5 мм до b = 15,3 мм.

Как и ранее, здесь при осуществлении моделирования в программной среде COMSOL Multiphysics 5.3 с количеством элементов порядка 2∙10⁵) при собственных размерах самой системы габаритом 1,24х0,3х0,13 м размеры области, окружающей данную магнитную систему (рис.4), выбирали существенно больше – это параллелепипед размерами 6х4х4 м.

Результаты моделирования отражались в виде той или иной координатной зависимости индукции B (т.е. индукции B в точках, удаленных на расстояние x от оси симметрии межполюсной области – вдоль линии действия пондеромоторной силы) при разных расстояниях между полюсами b и разных значениях тока питания катушек I.

На рис.5 и рис.6 показаны модельные координатные характеристики индукции B между полюсами при разных расстояниях между ними b и разных значениях величины тока I. Для их получения, что уже оговорено выше, использовалась экспериментальная полевая зависимость индукции E (рис.2) для соответствующей стали.

Как это видно на рис.5 и рис.6, полученные модельные координатные зависимости индукции B – извилистые, с перегибом, причем наблюдающимся при разных значениях и параметра b, и параметра I. Это значит, что их последующее дифференцирование, которое необходимо осуществить для получения соответствующих координатных характеристик градиента (вдоль x), всегда продемонстрирует наличие экстремумов, в окрестности которых и локализуется та или иная зона относительно стабильного градиента, приемлемая для размещения в ней изучаемого образца.

Используя возможности моделирования, важно было также выяснить, в какой мере содержание в стали одного из таких основных элементов, существенно влияющих на магнитные свойства стали, как углерод [11], могут оказывать влияние и на координатную характеристику индукции в межполюсной области между стальными полюсами. С этой целью использованы имеющиеся в [11] две, несколько отличающиеся друг от друга, полевые зависимости индукции в стали, показанные на рис.7 – с содержанием углерода 0,1 % и 0,3 %.

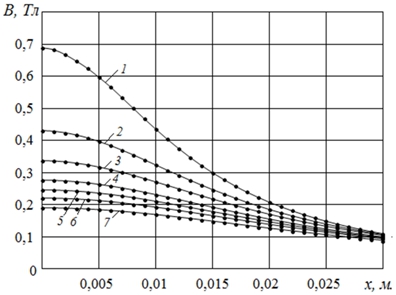
Рис. 5 – Модельные координатные характеристики индукции между полюсами при величине тока питания катушек 4A и различных расстояниях между полюсами b: 1 – b = 3,5мм; 2 – b = 6мм; 3 – b = 8мм; 4 – b = 10мм; 5 – b = 11,5мм; 6 – b = 13мм; 7 – b = 15,3мм

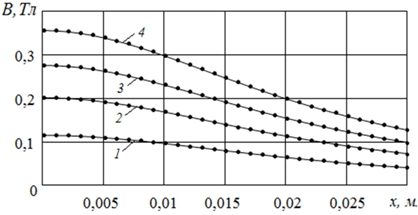
Рис. 6 – Модельные координатные характеристики индукции между полюсами при межполюсном расстоянии 10мм и различных значениях величины тока питания катушек I: 1 – I = 1A; 2 – I = 2A; 3 – I = 4A; 4 – I = 7,5A

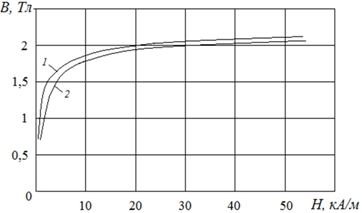
Рис. 7 – Экспериментальные кривые намагничивания стали (по [11]): 1 и 2 – соответственно с содержанием углерода 0,1% и 0,3%

 

Соответствующее моделирование приводит к результату, согласно которому взаимное отличие получаемых координатных характеристик индукции (кривые 1 и 2 на рис.8) не превышает 7 %. Это означает, что роль «сортности» стали, из которой может быть изготовлен магнитопровод магнетометра Фарадея, в известных пределах не оказывает существенного влияния на ключевую координатную характеристику индукции в межполюсной области магнетометра.

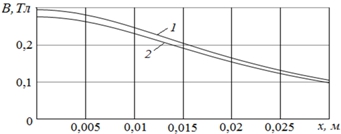
Рис. 8 – Модельные координатные характеристики индукции между полюсами магнетометра (рис.6, I = 4A, b = 10мм), полученные для случаев, если бы при изготовлении магнитопровода магнетометра использовалась сталь согласно данным рис.9; 1 и 2 – с содержанием углерода 0,1% и 0,3%

Благодарности Исследование выполнено при финансовой поддержке Министер-ства образования и науки Россий-ской Федерации по Госзаданию в сфере научной деятельности № 9.9626.2017.	Acknowledgement The research is conducted with financial support from the Russian Federation Ministry of Education and Science No 9.9626.2017.
Конфликт интересов Не указан.	Conflict of Interest None declared.

Список литературы/ References

1. Baskar D. High temperature Faraday balance for in situ measurement of magnetization in transition metal oxides / Baskar D., Adler S.B. // Review of Scientific Instruments. – 2007. – V. 78. – P. 023908.
2. Bombik A. Magnetic susceptibility of powder and single-crystal TmFeO3 orthoferrite / A. Bombik, B. Leśniewska, A.W. Pacyna // Journal of Magnetism and Magnetic Materials. – 2000. – V. 214. – P. 243–250.
3. Gopalakrishnan R. Magnetic susceptibility measurements on fly ash admixtured cement hydrated with groundwater and seawater / R. Gopalakrishnan, S. Barathan, D. Govindarajan // American Journal of Materials Science. – 2012. – № 2 (1). – P. 32–36.
4. Zhang C.P. Crystalline phase transition information induced by high tem-perature susceptibility transformations in bulk PMP-YBCO superconductor growth in-situ / C.P. Zhang, X. Chaud, E. Beaugnon, et al. // Physica C. – 2015. – V. 508. – P. 25–30.
5. Sandulyak A.V. The approach to the creation and identification of the positioning zone of the sample in the Faraday magnetometer / A.V. Sandulyak, A.A. Sandulyak, M.N. Polismakova, D.A. Sandulyak, V.A. Ershova // Journal of Magnetism and Magnetic Materials. – 2018. – V. 469. – P. 665–673.
6. Сандуляк А.А. Использование полюсных наконечников сферической формы для реализации метода Фарадея / А.А. Сандуляк, А.В. Сандуляк, М.Н. Полисмакова, Д.О. Киселев, В.А. Ершова, Д.А. Сандуляк // Приборы и техника эксперимента. – 2018. – № 1. – С. 109–112.
7. Сандуляк А.В. Магнетометр Фарадея с полюсными наконечниками-полусферами: идентификация зоны стабильного силового фактора / А.В. Сандуляк, А.А. Сандуляк, М.Н. Полисмакова, Д.О. Киселев, Д.А. Сандуляк // Российский технологический журнал. – 2017. – Т. 5. – № 6. – С. 43–54.
8. Кифер И.И. Испытания ферромагнитных материалов. / И. И. Кифер – М.: Энергия, 1969. – 360 с.
9. Сандуляк А.В. Очистка жидкостей в магнитном поле. / А.В Сандуляк – Изд. при Львовском ун-те, 1984. – 167с.
10. Потапов Л.А. COMSOL Multiphysics: моделирование электромеханических устройств. / Л.А. Потапов, И.Ю. Бутарев – Изд-во Брянского гос. тех. ун-та, 2011. – 113 с.
11. Справочник по электротехническим материалам. Т.2. Под общ. ред. К.А. Андрианова и др., М-Л: Госэнергоиздат, 1960. – 512 с.

Список литературы на английском языке / References in English

1. Baskar D. High-temperature Faraday balance for in situ measurements of magnetization in transition metal oxides / Baskar D., Adler S.B. // Review of Scientific Instruments. – 2007. – V. 78. – P. 023908.
2. Bombik A. Magnetic susceptibility of powder and single-crystal TmFeO3 orthoferrite / A. Bombik, B. Leśniewska, A.W. Pacyna // Journal of Magnetism and Magnetic Materials. – 2000. – V. 214. – P. 243–250.
3. Gopalakrishnan R. Magnetic susceptibility measurements on fly ash admixtured cement hydrated with groundwater and seawater / R. Gopalakrishnan, S. Barathan, D. Govindarajan // American Journal of Materials Science. – 2012. – № 2 (1). – P. 32–36.
4. Zhang C.P. Crystalline phase transition information induced by high tem-perature susceptibility transformations in bulk PMP-YBCO superconductor growth in-situ / C.P. Zhang, X. Chaud, E. Beaugnon, et al. // Physica C. – 2015. – V. 508. – P. 25–30.
5. Sandulyak A.V. The approach to the creation and identification of the positioning zone of the sample in the Faraday magnetometer / A.V. Sandulyak, A.A. Sandulyak, M.N. Polismakova, D.A. Sandulyak, V.A. Ershova // Journal of Magnetism and Magnetic Materials. – 2018. – V. 469. – P. 665–673.
6. Sandulyak А.А. Ispol'zovaniye polyusnykh nakonechnikov sfericheskoy formy dlya realizatsii metoda Faradeya [The Use of Spherical Pole Pieces For Performing the Faraday Balance Method] / A.A. Sandulyak, A.V. Sandulyak, M.N. Polismakova, D.O. Kiselev, V.A. Ershova, D.A. Sandulyak // Pribory i tekhnika eksperimenta [Instruments and Experimental Techniques]. – 2018. – V. 61. – No. 1. – P. 123–126. [in Russian]
7. Sandulyak А.V. Magnetometr Faradeya s polyusnymi nakonechnikami-polusferami: identifikatsiya zony stabil'nogo silovogo faktora [Faraday magnetometer with sheric pole pieces: identification zone with a stable force factor] / А.V. Sandulyak, А.А. Sandulyak, M.N. Polismakova, D.O. Kiselev, V.A. Ershova, D.A. Sandulyak // Rossiyskiy tekhnologicheskiy zhurnal [Russian Technological Journal] – 2017. – V. 5. – № 6. – P. 43–54. [in Russian]
8. Kifer I.I. Ispytaniya ferromagnitnykh materialov [Testing of ferromagnetic materials] / I.I. Kifer – Moscow, Energy, 1969. – P. 360. [in Russian].
9. Sandulyak A.V. Ochistka zhidkostey v magnitnom pole [Purification of Liquids in Magnetic Field]. / A.V. Sandulyak – High School, Lvov, 1984. – P. 167. [in Russian].
10. Potapov L.A. COMSOL Multiphysics: modelirovaniye elektromekhanicheskikh ustroystv. [COMSOL Multiphysics: modeling of electromechanichal assemblies]. – Publ. by Bryansk state techn. Univ., 2011. – P. 113. [in Russian].
11. Spravochnik po elektrotekhnicheskim materialam. [Electrotechnical materials reference guide. Т.2]. Under general editorship of K.A. Adrianova et al. Moscow – Leningrad: Gosenergoizdat, 1960. – P. 512. [in Russian].