ЗАВИСИМОСТЬ ДАВЛЕНИЯ НА ВАЛКИ ПРОФИЛЕГИБОЧНОГО СТАНА ОТ НЕКОТОРЫХ ПАРАМЕТРОВ ПРОФИЛИРОВАНИЯ

Манжурин И.П.¹, Сидорина Е.А.²

¹Профессор, кандидат технических наук, ² Магистр технических наук,

Карагандинский государственный технический университет г. Караганда

ЗАВИСИМОСТЬ ДАВЛЕНИЯ НА ВАЛКИ ПРОФИЛЕГИБОЧНОГО СТАНА ОТ НЕКОТОРЫХ ПАРАМЕТРОВ ПРОФИЛИРОВАНИЯ

Аннотация

В статье приведены результаты исследования зависимости давления на валки профилегибочного стана от некоторых технологических параметров профилирования. При изгибе полосы в валках профилегибочного стана одними из основных параметров являются: угол подгибки элементов профиля, радиус изгиба (относительный), ширина подгибаемого элемента профиля, настройка стана (относительный зазор между валками) и другие факторы. Влияние указанных параметров исследовано с использованием  теории математической обработки эксперимента, в частности  корреляционно-регрессионного анализа. Приведены экспериментальные и расчетные линии регрессии, для последних приведены расчетные уравнения  регрессии с указанием коэффициентов  достоверности аппроксимации  экспериментальных данных.

Ключевые слова: давление, корреляционно-регрессионный анализ, коэффициенты  достоверности аппроксимации,  закон распределения.

Manzhurin I.P.¹, Sidorina E.A.²

¹Professor, PhD in Engineering, ²Master of Engineering,

Karaganda State Technical University of Karaganda

DEPENDENCE OF PRESSURE ON SHAFTS OF PROFILE BENDING MACHINE FROM SOME PARAMETERS OF PROFILING

Abstract

The article presents the results of the study of pressure dependence on the shafts of profile bending machines from certain technological parameters of profiling. When bending a strip in the shafts of the profile bending machines, one of the main parameters is the angle of the bend of the profile elements, the bending radius (relative), the width of the bent profile member, the mill setting (the relative gap between the rollers), and other factors. The influence of these parameters was investigated using the theory of mathematical processing of the experiment, in particular, correlation-regression analysis. The experimental and calculated regression lines are presented, for the latter the calculated regression equations with the coefficients of reliability of the approximation of the experimental data are given.

Keywords: pressure, correlation-regression analysis, coefficients of reliability of approximation, distribution law.

Давление на валки профилегибочного стана имеет разные значения при различных условиях производства гнутых профилей. Оно зависит не только от толщины исходной заготовки и радиуса изгиба, но и от других параметров: ширины подгибаемых элементов, диаметров валков, углов подгибки, настройки стана, свойств материала и др. Решить столь сложную задачу по учету влияния всех факторов с помощью общей теории пластичности, не делая серьезных допущений, довольно затруднительно. Вопрос усложняется еще и тем, что влияние указанных факторов, большинство из которых носит статистический характер, различно по величине и направлению. Все это определяет давление на валки как стохастическую переменную величину.

Стохастическая величина, в рассматриваемом случае давление на валки, полностью может быть описана, если известен закон ее распределения, т.е. соотношение, устанавливающее связь между возможными значениями переменной величины и соответствующими им вероятностями. Закон распределения может быть установлен на основе анализа статистического материала.  С этой целью было проанализировано 526 значений давления при профилировании уголков и швеллеров из полосы толщиной t₀=1÷5 мм из углеродистых и низколегированных сталей по единичным маршрутам с углами подгибки α=0˚-15˚; α=0˚-30˚; α=0˚-45˚; α=0˚-60˚;  α=0˚-75˚;  α=0˚-90˚ при  относительном радиусе изгиба  =0,5÷8,  ширине подгибаемой полки b =50÷350 мм при различной настройке стана  (где r-радиус изгиба, мм; s-зазор между валками, мм).

Интервальный ряд для усилий с величиной интервала i=5,3 кН приведен в таблице 1.

Таблица 1 – Интервальный ряд распределения Р

№ п/п	Интервалы, Р,кН	Частота
		Абсолютная ni	Относительная ωi
1	2	3	4
1.	0 ÷ 5,3	115	0,2186
2.	5,3 ÷10,6	174	0,3308
3.	10,6 ÷ 15,9	118	0,2243
4.	15,9 ÷ 21,2	60	0,1140
5.	21,2 ÷26,5	21	0,0400
6.	26,5 ÷ 31,8	16	0,0304
7.	31,8 ÷ 37,1	12	0,0228
8.	37,1 ÷ 42,4	5	0,0095
9.	42,4 ÷ 47,7	2	0,0038
10.	47,7 ÷ 53	2	0,0038
11.	53,0 ÷ 58,3	1	0,0019
	Σ	526	0,9999

 

По данным табл.1 построены гистограмма и полигон распределения, приведенные на рис.1.

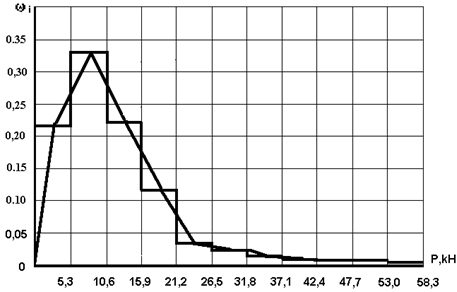
Рис. 1 – Гистограмма и полигон распределения усилия на валки стана

 

По данным табл.1 рассчитаны основные статистики ряда распределения:

первый центральный момент (оценка математического ожидания) μ₁ =11,77 кН;

второй центральный момент (оценка дисперсии) μ₂ =76,46;

третий центральный момент 

четвертый центральный момент .

Показатель отклонения распределения от симметричного его вида – асимметрия A – определяется  соотношением .  В качестве характеристики большего или меньшего подъема графика по сравнению с нормальной кривой распределения (кривой Гаусса) является эксцесс:

. Оценки дисперсий асимметрии D(A) и эксцесса D(E) определяются соотношениями:

и соответственно равны A=1,685; E=3,801, а среднеквадратичные отклонения .

Возвращаясь к закону распределения необходимо отметить, что некоторая функция от исследуемой величины x, распределенной асимметрично, например x², lgx и др. приближенно следует нормальному закону. Функциональное преобразование P в lgP позволило получить ряд распределения lgP, представленный в таблице 2.

Таблица 2 – Интервальный ряд распределения

№ п/п	Интервалы  lgP	ni	ωi	pi
1	2	3	4	5
1	0,3572÷ 0,4893	22	0,0418	0,0475
2	0,4893 ÷ 0,6214	42	0,0800	0,0635
3	0,6214 ÷ 0,7535	64	0,1216	0,1093
4	0,735 ÷ 0,8856	75	0,1426	0,1538
5	0,8856 ÷ 1,0177	83	0,1578	0,1768
6	1,0177 ÷1,1498	87	0,1654	0,1671
7	1,1498 ÷ 1,2819	69	0,1311	0,1298
8	1,2819 ÷ 1,4140	43	0,0818	0,0822
9	1,4140 ÷ 1,5461	28	0,0532	0,0430
10	1,5461÷ 1,6782	10	0,0190	0,0182
11	1,6782 ÷ 1,8103	3	0,0057	0,0064
	Σ	526	1,0000	0,9976

 

Статистики для ряда распределения lgP с интервалом i=0,1321 следующие: оценка математического ожидания x=0,9802; оценка дисперсии μ₂=4,949 или в единицах интервала ; оценка асимметрии A=0,107; оценка эксцесса E=- 0,6. В качестве первого  критерия  согласия  сравниваются рассчитанные оценки A и E с их  оценками дисперсий:

Распределение можно считать нормальным,  если  выборочные оценки асимметрии и эксцесса удовлетворят неравенствам:

Следовательно, гипотезу о нормальном  распределении lgP можно считать правильной. Плотность распределения p_i (колонка 5, табл.2) для  логарифмически нормального закона распределения определена  по таблице значений нормальной функции распределения.

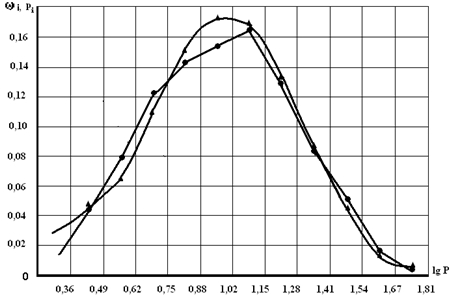
Рис. 2 – Экспериментальная и расчетная кривые распределения lgP

 

Для установления зависимости давления на валки стана,  исходя из статистического (а не функционального) характера зависимости  давления от параметров профилирования, представляется целесообразным использовать методы, отвечающие характеру исследуемого процесса. В этой связи наиболее  эффективным является корреляционно-регрессионный анализ.

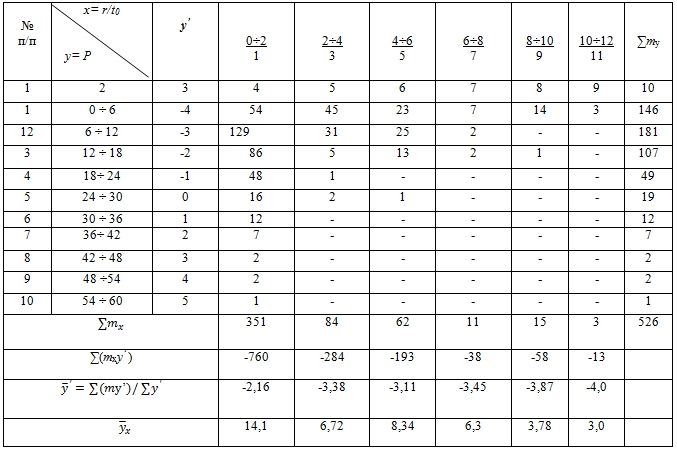
Данные,  необходимые для построения эмпирической линии регрессии зависимости P =f(r/t₀), приведены в табл.3.

В табл.3 относительные середины интервалов рассчитаны по уравнению  а средние значения давления Р по интервалам по формуле  -сумма , попавших в интервал.

 

Таблица 3 – Корреляционная таблица зависимости P от r/t₀

Примечание: во всех таблицах y^’-относительная середина интервала; m_y-сумма значений давления, попавших в интервал.

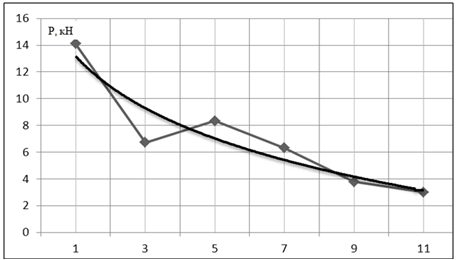
Рис. 3 – Экспериментальная и расчетная  линии регрессии

 

Экспериментальной линии регрессии (рис.3) следует, что с увеличением относительного радиуса изгиба примерно до r/t₀ ≈ 5÷6 давление уменьшается, а далее уменьшение Р  замедляется. Функция такого типа хорошо описывается уравнением логарифмического типа

    (1)

по которому  и построена расчетная линия регрессии (рис.3) c коэффициентом достоверности аппроксимации  R² =0,8715.

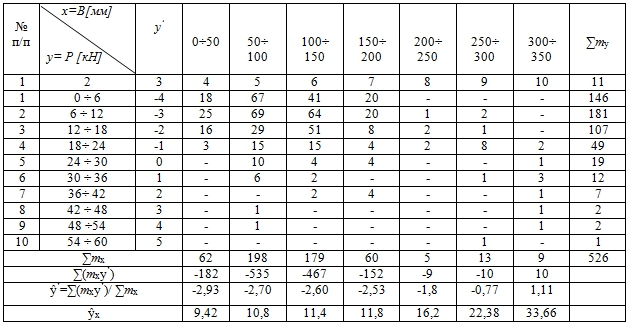
Таблица 4– Корреляционная таблица зависимости  Р от ширины полки В

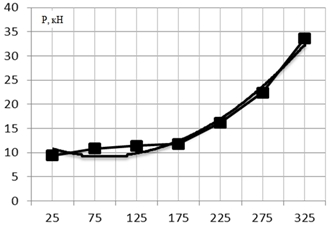
Рис. 4 – Экспериментальная и расчетная линии регрессии   зависимости давления от ширины подгибаемой полки

 

Нанесенные на график (рис.4) значения давления из корреляционной табл. 4 и построенная по ним эмпирическая линия регрессии, показывает, что зависимость Р от ширины подгибаемой полки может быть аппроксимирована квадратичной функцией – параболой второго порядка

     (2) коэффициент достоверности аппроксимации  R² =0,9761. Коэффициенты в уравнении (2)  рассчитаны по методу наименьших квадратов и  по нему же построена расчетная линия регрессии (рис.4). Зависимость давления от угла подгибки α⁰  представлена корреляционной табл.5 и на рис. 5.  

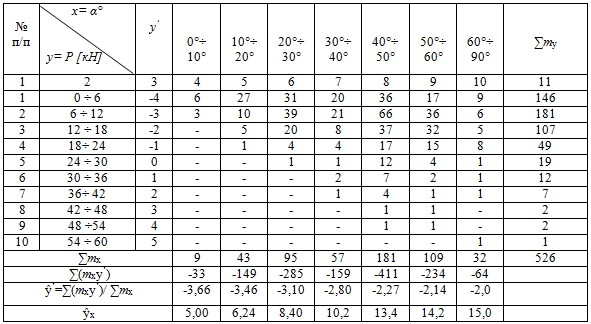
Таблица 5 – Зависимость давления от угла подгибки α⁰

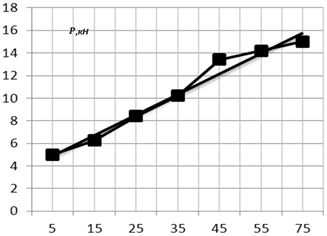
Рис. 5 – Экспериментальная и расчетная линии регрессии зависимости давления от угла подгибки

 

Расчетная линия регрессии построена по уравнению y=1,8186х+3,0743 с коэффициентом достоверности аппроксимации R²=0,9739.

Исследование зависимости давления от некоторых  параметров  профилирования позволяет применять другие методы математической обработки экспериментальных данных:  дисперсионный анализ, математическое планирование эксперимента и др. для изучения процесса профилирования.

Заключение

1.Информация о статистическом законе распределения давления на валки

профилегибочного стана позволяет использовать все методы математической обработки экспериментальных данных и известные критерии согласия.

2.По полученным в статье расчетным уравнениям регрессии можно рассчитать необходимые параметры профиля при разработке калибровки валков профилегибочного стана и выбрать его параметры.

Список литературы / References

1. Богоявленский К.Н. О вероятностно-статистическом анализе давления металла на валки профилегибочного стана / Богоявленский К.Н., Рис В.В., Манжурин И.П.// Тр.ЛПИ «Обработка металлов давлением».№ 322.Л.: Машиностроение. – 1971. – С. 31 – 34
2. Манжурин И.П. Определение утонения полосы :при профилировании ее в валках профилегибочного стана / Манжурин И.П., Сидорина Е.А. // ЗАО «Металлургиздат», Металлург. – 2012г. – С. 65 – 68.
3. Адлер Ю.П. Введение в планирование эксперимента / Адлер Ю.П.// М.:Металлургия. – 1969. – С. 157 - 161.
4. Адлер Ю.П. Планирование эксперимента при поиске оптимальных условий / Адлер Ю.П., Маркова Е.В., Грановский Ю.В. //. - М.: Наука. – 1971г. – С. 283 - 286.
5. Митропольский А.К. Техника статистических вычислений / Митропольский А.К. //.- М.: Наука. – С.490.
6. Вентцель Е.С. Теория вероятностей / Вентцель Е.С. //. - М.: Наука. – 571с.
7. Налимов В.В. Статистические методы планирования экстремальных экспериментов / Налимов В.В., Чернова Н.А. //. - М.: Наука.- 1965. – 340 с.
8. Налимов В.В. Теория эксперимента / Налимов В.В.// М.: Наука. - 1971. – 208 с.
9. Саутин С.Н. Планирование эксперимента в химии и химической технологии /Саутин С.Н.//. Л.: - Химия. – 1975. – 48 с.
10. Кикс Ч. Основные принципы планирования эксперимента / Кикс Ч.//. - М.: Мир. – 1967. – 407 с.
11. Хан Г. Статистические модели в инженерных задачах / Г.Хан, С.Шапиро //. -М.: Мир,-1969. -388 с.

Список литературы на английском языке / References in English

1. Bogojavlenskij K.N. O verojatnostno-statisticheskom analize davlenija metalla na valki profilegibochnogo stana [On the probabilistic statistical analysis of the metal pressure on the rolls of the roll forming mill] / Bogojavlenskij K.N., Ris V.V., Manzhurin I.P.// Tr.LPI «Obrabotka metallov davleniem».№ 322.L.: Mashinostroenie, 1971. – Р. 31 – 34. [in Russian]
2. Manzhurin I.P. Opredelenie utonenija polosy pri profilirovanii ee v valkah profilegibochnogo stana [Determination of band thinning when profiling it in the rolls of the roll forming mill] / Manzhurin I.P., Sidorina E.A. // ZAO «Metallurgizdat», Metallurg, 2012g. – Р. 65 – 68. [in Russian]
3. Adler Ju.P. Vvedenie v planirovanie jeksperimenta [Introduction to experiment planning] / Adler Ju.P.// M.:Metallurgija. 1969. - Р. 157 – 161. [in Russian]
4. Adler Ju.P. Planirovanie jeksperimenta pri poiske optimal'nyh uslovij [Planning an experiment when searching for optimal conditions] / Adler Ju.P., Markova E.V., Granovskij Ju.V. //. - M.: Nauka, 1971g. - Р. 283 - 286., [in Russian]
5. Mitropol'skij A.K. Tehnika statisticheskih vychislenij [The technique of statistical computations] / Mitropol'skij A.K. //.- M.: - Nauka, - Р. 490. [in Russian]
6. Ventcel' E.S. Teorija verojatnostej [Probability Theory] / Ventcel' E.S. //. - M.: Nauka, Р.571.
7. Nalimov V.V. Statisticheskie metody planirovanija jekstremal'nyh jeksperimentov [Statistical Methods for Planning Extreme Experiments] / Nalimov V.V., Chernova N.A. //. - M.: Nauka, 1965. – Р. 340. [in Russian]
8. Nalimov V.V. Teorija jeksperimenta [Theory of experiment] / Nalimov V.V.//. - M.: Nauka, - 1971. – Р. 208. [in Russian]
9. Sautin S.N. Planirovanie jeksperimenta v himii i himicheskoj tehnologii [Planning an experiment in chemistry and chemical technology] /Sautin S.N.//. L.: Himija. – 1975. – Р. 4. [in Russian]
10. Kiks Ch. Osnovnye principy planirovanija jeksperimenta [Basic principles of experiment planning] / Kiks Ch.//. - M.: Mir, - 1967. – Р.407. [in Russian]
11. Hahn J. Shapiro [Statistical models in engineering] / Gerald J.Hahn & Samuel S. Shapiro//.- М.:Mir,-1969.-P.388. [in Russian]