ИССЛЕДОВАНИЕ РЕШЕНИЯ КРАЕВОЙ ЗАДАЧИ РИМАНА НА ЛУЧЕ С БЕСКОНЕЧНЫМ ИНДЕКСОМ НОВЫМ МЕТОДОМ

Салимов Р.Б.¹, Горская Т.Ю.²

¹ORCID: 0000-0003-4177-4830, Доктор физико-математических наук, ²ORCID: 0000-0001-7136-8388, Кандидат технических наук,

^1,2Казанский государственный архитектурно-строительный университет, г. Казань

ИССЛЕДОВАНИЕ РЕШЕНИЯ КРАЕВОЙ ЗАДАЧИ РИМАНА НА ЛУЧЕ С БЕСКОНЕЧНЫМ ИНДЕКСОМ НОВЫМ МЕТОДОМ

Аннотация

В работе рассматривается краевая задача Римана с бесконечным индексом дробного порядка, превышающего половину и меньшего единицы, когда краевое условие для искомой аналитической функции задается на положительной действительной оси комплексной плоскости. Для решения задачи используется подход, основанный на устранении бесконечного разрыва аргумента коэффициента краевого условия с помощью специально подобранной аналитической функции, представляющей собой показательную функцию с названной дробной степенью аргумента.

Ключевые слова: краевая задача Римана, аналитическая функция, бесконечный индекс.

Salimov R.B.¹, Gorskaya T.Yu.²

¹ORCID: 0000-0003-4177-4830, PhD in Physics and Mathematics, ²ORCID: 0000-0001-7136-8388, PhD in Engineering,

^1,2Kazan State University of Architecture and Civil Engineering, Kazan

INVESTIGATION OF SOLUTION OF RIEMANN BOUNDARY VALUE PROBLEM ON RAY WITH INFINITE INDEX WITH NEW METHOD

Abstract

In this paper we consider the Riemann boundary value problem with an infinite fractional index exceeding half and less than one when the boundary condition for the desired analytic function is given on the positive real axis of the complex plane. To solve the problem, the approach based on eliminating an infinite discontinuity of the argument of the coefficient of the boundary condition using a specially selected analytic function representing an exponential function with the fractional power of the argument is used.

Keywords: Riemann boundary value problem, analytic function, infinite index.

Введение. Постановка задачи

Пусть область в плоскости комплексного переменного   границей которой служит положительная действительная полуось L. Требуется определить функцию Ф(z) аналитическую и ограниченную в области D, если её граничные значения удовлетворяют условию

   (1)

где  предельные значения функции Ф(z) при z→t соответственно слева и справа, когда соответственно  -заданная функция, удовлетворяющая условию Гельдера на  коэффициент G(t) заданная функция, обладающая следующими свойствами

   (2)

заданные числа,  заданная функция,  Задача с краевым условием (1) называется неоднородной, а задача с краевым условием    (3)

однородной [1 C.106], [2 C.122, 133].

В статье [3] дано решение однородной задачи Римана в случае, когда   путем устранения бесконечного разрыва  с помощью специально подобранной аналитической функции. Оно отличается простотой и прозрачностью по сравнению с решением, разработанным Н.В. Говоровым – основателем научного направления, посвященного задачам Римана с бесконечным индексом [4 С. 113-123].

Краткие сведения о развитии этого научного направления приведены в работе [3], в которой, в частности, упоминаются работы Толочко М.Э. [5], Сандрыгайло И.Е. [6], Алехно А.Г. [7].

Основные результаты

В данной работе подход, примененный в статье [3], распространяется на случай, когда 

Возьмем функцию

,  однозначную и аналитическую в области D, граничные значения которой  (обозначенные как и в случае Ф(z)) удовлетворяют равенству

    (4)

причем    (5) Для  имеем в частности     (6)

Рассмотрим вначале решение однородной задачи с краевым условием (3). Не ограничивая общности, для простоты примем

   (7)

Запишем краевое условие (3) в виде    (8)

В силу соотношений (2), (4), (8) будем иметь  причем . Следовательно, задача (7) есть задача с коэффициентом G1(t)  удовлетворяющим условию H_L.

Определим аналитическую и ограниченную в области D  функцию [1 С. 119],

значения которой на  удовлетворяют условию  В последней формуле интеграл можно заменить интегралом по всей действительной оси, считая   когда плотность  удовлетворяет условию Гельдера на этой оси, поэтому 

Функция  является аналитической в области D и ее граничные значения удовлетворяют условию . Выражая отсюда G1(t) краевое условие (7) запишем так

Это означает, что функция  является аналитической всюду с плоскости   так как её значения на берегах разреза по линии L  совпадают, т.е. она представляет собой целую функцию F(z)  Итак

   (9)

Так как   функции, ограниченные в области  то    (10) для всех точек области D включая точки L Поэтому в силу (9) с учетом (5) будем иметь      (11) причем ,  поскольку  и с учетом (6) получаем

Принимая во внимание (10), легко убедиться в том, что порядок p_F целой функции F(z)  формулы (9) подчиняется условию

где  При  в силу (11) имеем

что невозможно, если F(z) целая функция конечного порядка p_F и конечного типа [8 С.259].

В дальнейшем будем рассматривать решения задачи (3) в классе функций, содержащих согласно (9) целые функции F(z) конечного порядка и конечного типа, считая 

Таким образом, справедлива

Теорема 1. Если краевая задача (3) при  имеет ограниченное решение в указанном классе функций, то это решение определяется формулой

    (13)

где F(z) -произвольная целая функция порядка  конечного типа, удовлетворяющая неравенствам (11), (12).

Можно показать, что, в частности, в качестве F(z) можно взять целую функцию с положительными нулями, выбрав соответствующим образом положение последних.

Нетрудно убедиться в том, что справедлива и обратная

Теорема 2. Если  то ограниченное решение задачи (3) определяется формулой (13), где F(z) произвольная целая функция порядка  конечного типа, удовлетворяющая неравенствам (11), (12).

Для доказательства вначале отметим, что функция (13) по построению удовлетворяет краевому условию (3). Остается установить ограниченность функции (13).

Функция  является ограниченной в области D (вместе с функцией Г(z) ), следовательно,

для всех точек области D включая точки L. Поэтому для функции (13) на основании (6), (12) будем иметь и в силу (5), (11) получим

Следовательно, функция Ф(z) ограничена на всей действительной оси.

В силу (13) порядок функции Ф(z) в верхней полуплоскости меньше числа . Поэтому на основании теоремы Фрагмена-Линделефа приходим к выводу , что  всюду в верхней полуплоскости. Ясно, что сказанное относится и к точкам нижней полуплоскости. Следовательно, функция Ф(z) ограничена в области D, что и требовалось.

Для решения неоднородной задачи краевое условие (1) умножим на коэффициент как и выше, представим в виде  и краевое условие (1) запишем так

     (14)

принимая для простоты 

Мы пришли к задаче о скачке для функции  аналитической в области D [1 С.106,109],  [2, C. 112, 113].

Ограниченное в области D (частное) решение   задачи (14) определяется формулой

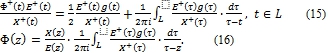Поэтому Из формулы (15) видно, что если      (17)

то  будет ограниченной функцией, т.к. при  согласно (5) . При этом функция Ф(z) формулы (16) будет ограниченной в области D поскольку в силу (6)  и порядок Ф(z) в полуплоскости  меньше единицы. Таким образом, мы пришли к

Теореме 3. Если выполняется условие (17), то неоднородная задача (1) имеет ограниченное частное решение, определяемое формулой (16).

При  согласно (5) имеем  отпадает необходимость выполнения условия (17), и искомое частное решение задачи (1) определяется формулой (16). Случай  рассмотрен в работе [10].

Уместно остановиться на другом способе получения при  частного решения неоднородной задачи (1), когда не используется условие (17). Для этого возьмем решение задачи о скачке (14), определяемое формулой

   (18)

где  -произвольная целая функция порядка , которая при  удовлетворяет условию, аналогичному (12)

   (19)

Здесь имеем    (20) где причем  при  [1 С.49], [2 С. 66,68]. Пусть функция   выбрана так, что     (21)

Тогда на основании (20) приходим к заключению, что  является функцией, ограниченной на L. Согласно (18) имеем

    (22)

Интеграл этой формулы есть ограниченная в области D функция, стремящаяся к нулю при . С учетом (6) и (19) при  приходим к выводу, что функция  является ограниченной на отрицательной части действительной оси.

Порядок функции Ф(z) формулы (22) в полуплоскости  не превышает  Следовательно, из ограниченности этой функции на всей действительной оси втекает её ограниченность в каждой из указанных полуплоскостей и ограниченность в области D

Итак, справедлива

Теорема 4. Если   целая функция порядка , выбранная так, чтобы выполнялось условие (21) и неравенство (19) при  то частное решение неоднородной задачи (1) определяется формулой (22).

Общее решение неоднородной задачи (1) как известно, представляется как сумма частного решения этой задачи и общего решения соответствующей однородной задачи (3).

Вопрос о построении удовлетворяющей условиям теоремы 4 целой функции  требует специального рассмотрения.

Заключение

В данной работе получено новое прозрачное решение рассматриваемой задачи. Это решение отличается в деталях от соответствующих результатов работы [4], что объясняется, в частности, тем, что постановки задач в указанных работах имеют некоторые различия и кроме того используются разные методы решения задачи, приводящие к разным формулам.

Список литературы / References

1. Гахов Ф.Д. Краевые задачи / Ф.Д. Гахов. – М.: Наука, 1977. – 641 с.
2. Мусхелишвили Н.И. Сингулярные интегральные уравнения / Н.И. Мусхелишвили. – М.: Наука, 1968. – 511 с.
3. Салимов Р.Б. Новый подход к решению однородной краевой задачи Римана на луче с бесконечным индексом / Р.Б. Салимов, А.З. Сулейманов // Известия вузов. Математика. №5, 2017, С. 71 – 76.
4. Говоров Н.В. Краевая задача Римана с бесконечным индексом / Н.В. Говоров. – М.: Наука, 1986. – 239 с.
5. Толочко М.Э. О разрешимости однородной краевой задачи Римана с бесконечным индексом для полуплоскости/ М.Э. Толочко // Известия АН БССР, сер. Физ.-матем. Наук, №5, 1972. С. 34 – 41.
6. Сандрыгайло И.Е. О краевой задаче Римана с бесконечным индексом для полуплоскости/ И.Е. Сандрыгайло // Доклады АН БССР 19(10), 1975, С. 872 – 875.
7. Алехно А.Г. Достаточные условия разрешимости однородной краевой задачи Римана с бесконечным индексом / А.Г. Алехно // Труды Математического центра имени Н.И. Лобачевского. Т.14. Казань, 2002. С. 71 – 77.
8. Маркушевич А.И. Теория аналитических функций / А.И. Маркушевич. Т. 2. – М.: Наука, 1968. – 624 с.
9. Левин Б.Я. Распределение корней целых функций / Б.Я. Левин. –М.: Гостехиздат, 1956. – 632 с.
10. Салимов Р.Б. Решение неоднородной краевой задачи Римана на луче с бесконечным индексом новым методом / Р.Б. Салимов, А.З. Сулейманов // Труды Математического центра имени Н.И. Лобачевского. Т.54. Казань, 2017. С. 317 – 320.

Список литературы на английском языке / References in English

1. Gahov F.D. Kraevye zadachi [Boundary value problems] M.: Nauka, 1977. – 641 p. [in Russian]
2. Mushelishvili N.I. Singuljarnye integral'nye uravnenija. [Singular integral equations] M.: Nauka, 1968. – 511 p. [in Russian]
3. Salimov R.B. Novyj podhod k resheniju odnorodnoj kraevoj zadachi Rimana na luche s beskonechnym indeksom [A new approach to the solution of a homogeneous boundary value problem of Riemann on the beam with infinite index] // Izvestija vuzov. Matematika. [Izvestiya vuzov. Math] – №5, 2017, P. 71 – 76. [in Russian]
4. Govorov N.V. Kraevaja zadacha Rimana s beskonechnym indeksom [The Riemann boundary value problem with infinite index] M.: Nauka, 1986. – 239 p. [in Russian]
5. Tolochko M.Je. O razreshimosti odnorodnoj kraevoj zadachi Rimana s beskonechnym indeksom dlja poluploskosti [On solvability of the homogeneous boundary value Riemann problem with an infinite index for half-plane ] / M.Je. Tolochko // Izvestija AN BSSR, ser. Fiz.-matem. Nauk [Izvestia an BSSR, ser. Phys.-mod. Sciences], №5, 1972. P. 34 – 41. [in Russian]
6. Sandrygajlo I.E. O kraevoj zadache Rimana s beskonechnym indeksom dlja poluploskosti [On the boundary Riemann problem with an infinite index for half-plane] / I.E. Sandrygajlo // Doklady AN BSSR [Doklady an BSSR] 19(10), 1975, P. 872 – 875. [in Russian]
7. Alehno A.G. Dostatochnye uslovija razreshimosti odnorodnoj kraevoj zadachi Rimana s beskonechnym indeksom [Sufficient conditions of solvability of the homogeneous boundary value Riemann problem with an infinite index] / A.G. Alehno // Trudy Matematicheskogo centra imeni N.I. Lobachevskogo. [Works of Mathematical center named after N. And. Lobachevsky ] T.14. Kazan', 2002. P. 71 – 77. [in Russian]
8. Markushevich A.I. Teorija analiticheskih funkcij [The theory of analytic functions] T. 2. M.: Nauka, 1968. – 624 p. [in Russian]
9. Levin B.Ja. Raspredelenie kornej celyh funkcij [The distribution of roots of entire functions] M.: Gostehizdat, 1956. – 632 p. [in Russian]
10. Salimov R.B. Reshenie neodnorodnoj kraevoj zadachi Rimana na luche s beskonechnym indeksom novym metodom [Solution of the inhomogeneous boundary value problem of Riemann on the beam with infinite index a new method] // Trudy Matematicheskogo centra imeni N.I. Lobachevskogo. [Works of Mathematical center named after N. And. Lobachevsky] T.54. Kazan', 2017. P. 317 – 320. [in Russian]