CREATIVE TASKS AS MEANS OF ACTIVATION OF STUDENTS' COGNITIVE ACTIVITY

Новиков П.В.

Кандидат психологических наук, профессор кафедры социально-экономических дисциплин Саранского кооперативного института

ТВОРЧЕСКИЕ ЗАДАНИЯ КАК СРЕДСТВО АКТИВИЗАЦИИ ПОЗНАВАТЕЛЬНОЙ ДЕЯТЕЛЬНОСТИ УЧАЩИХСЯ

Аннотация

Статья посвящена развитию мыслительных действий и познавательной активности учащихся.  Дается описание заданий, развивающих мышление и интеллектуальную активность учащихся.  Охарактеризованы требования, необходимые для разработки творческих заданий. Рассмотрены  проявления особенностей мыслительных действий учащихся, проявляющиеся при решении нестандартных задач. Отмечается, что педагог  должен уметь решать задачи не только предметного обучения, но и владеть психотехнологиями интеллектуального и личностного развития учащихся.

Ключевые слова: мышление, мыслительные способности, познавательная активность, развивающие задания, условия развития творческого мышления.

Novikov P.V.

PhD in Psychology, professor of the Department of social and economic disciplines, Saransk Cooperative Institute

CREATIVE TASKS AS MEANS OF ACTIVATION OF STUDENTS' COGNITIVE ACTIVITY

Abstract

The article is devoted to the development of students’ mental operations and cognitive activity. The description of tasks, developing thinking and intellectual activity of students are presented. We characterize the requirements necessary for the development of creative tasks. Mental peculiarities of students actions that appear at the solution of non-standard tasks are considered. It is noted that the teacher should be able to decide the tasks not only of the subject learning, but also possess psychological technologies of intelligent and personal development of pupils.

Keywords: thinking, thinking ability, cognitive activity, educational tasks, conditions of development of creative thinking.

Творческое, самостоятельное мышление все чаще рассматривается как универсальная спо­собность, обеспечивающая успешное выполнение самых разнооб­разных видов деятельности. Развитие творческого мышления, таким образом, представляет собой од­ну из центральных линий личностного развития, именно оно по­зволяет человеку проявить свою индивидуальность и уникальность. Сейчас особенно важно, чтобы обучение в школе (и в вузе) становилось источником не только «технологической» оснащенности, но и личностного роста и, прежде всего, интеллектуально-творческого развития [1].

Формирование самостоятельности, креативности в мышлении, активности в поиске путей достижения поставленной цели предполагает решение учащимися (помимо учебных) нетиповых, нестандартных задач, имеющих иногда несколько способов решения, хотя и правильных, но в разной степени оптимальных. Для того чтобы решение таких задач способствовало действительному развитию активного, поискового мышления, оно должно быть организовано особым образом.

Чтобы сформировать у школьников полноценное мышление, необходимо в годы учебы уделять особое внимание направленному формированию у них фундаментальных мыслительных способностей  –  анализа, рефлексии, гибкости, оригинальности.

При разработке и проведении развивающих, творческих заданий следует учитывать требования: 1. Необходимо обеспечить «принятие» учащимися поставленной задачи. Для этого разрабатывается специальная вводная беседа, которая облегчает вхождение школьников в проблему, понимание ее смысла. 2. Важным показателем развития мышления учащихся является различная степень их самостоятельности при нахождении обобщенных способов решения новых задач. Поэтому необходимо определять не только зону актуального развития мыслительного действия учащихся, но и зону их ближайшего развития. С этой целью разрабатывается серия вспомогательных задач, которые последовательно предъявляются учащимся в том случае, если они не могут решить основную задачу [2, С.113].

Любая задача предполагает наличие некоторых условий, которые должен учитывать решающий, если он не желает допустить ошибку. Умение учитывать все необходимые условия, сопровождающие решение задачи, есть умение рефлексировать. Упущение какого-либо условия рефлексирования при решении задачи приводит к ее ошибочному решению или незавершенности. В таких случаях следующий шаг в смысле развития  можно осуществить  с помощью подсказки. Подсказка выступает как бы призывом   к повторному рефлексированию. Общая подсказка типа «Решите задачу еще раз», «Проверьте решение» содержит указание на необходимость учета всех условий  рефлексирования. Подобные подсказки способствуют самостоятельному выделению учащимися необходимых и не учтенных им в первый раз условий рефлексирования, поэтому положительное реагирование на них подтверждает  наличие исследуемого уровня развития мышления. Содержательная подсказка прямо указывает не необходимое и не учтенное условие рефлексирования. Прямая подсказка представляет собой указание на необходимость выполнения некоторых промежуточных действий, консультацию по невоспроизводимой в данный момент нужной информации. Принятие такого указания будет свидетельствовать об успешности используемого частного методического приема на пути обучения учащегося  некоторому способу решения задачи или формирования навыка.

С целью развития творческого мышления и активизации мыслительной деятельности учащихся автором разработана серия развивающих заданий [2], [3]. В качестве примера рассмотрим некоторые из них.

Задание «Площади». Инструкция учащимся: «Вам нужно вычислить площади 10 геометрических фигур (количество фигур в задании может быть различным). Для вычисления площадей данных фигур достаточно знать, как вычисляются площади квадрата и прямоугольника. Напоминаем, как вычисляются площади квадрата и прямоугольника. Задачи нужно решать оптимальным способом. Если возникают вопросы, обсуждаем в индивидуальном порядке».

Нечетные задачи  включают в себя  разные фигуры, каждую из которых, в результате преобразования можно превратить в квадрат. Площади всех фигур в нечетных задачах одинаковы. Четные задачи содержат тоже разные фигуры, которые можно преобразовать в прямоугольники. Площади всех фигур в четных задачах также одинаковые.

Задачи можно решать эмпирическим способом, когда каждая фигура разбивается на несколько фигур (в виде квадратов и прямоугольников). Затем вычисляется площадь каждой фигуры и все площади суммируются. В данном случае каждую задачу (нахождение площади очередной фигуры) ученик решает, как новую. Такой способ вычисления нерациональный, требует много времени, разных вычислений, допускается много ошибок в вычислениях.

В то же время, задачи могут решаться теоретическим способом, когда в ходе решения какой-то задачи ученик может выявить общий принцип их построения, который состоит в том, что фигуры в нечетных задачах преобразуются в квадрат, а фигуры в четных задачах преобразуются в прямоугольник, Это наиболее оптимальный способ решения. При таком способе решения не нужны конкретные вычисления. Достаточно вычислить площади фигур № 1 и № 2 и после проведенного анализа преобразовать фигуры в прямоугольник или в квадрат. Если учащиеся долго не могут решить задачи, то им даются подсказки. Подсказка №1: Подумай, задачи можно решить другим, более оптимальным способом. Подсказка №2: Можно ли эти фигуры как-то преобразовать в другие    фигуры. Подсказка №3: Можно ли фигуры превратить в квадрат (или прямоугольник).

Задание «Площади» проводилось с учащимися 7-х – 11-х классов. Только около 8 % школьников смогли решить задачи теоретическим способом. Основная часть учащихся применяли не эффективный способ решения.

Важной характеристикой самостоятельного мышления является его гибкость.  Гибкость ума проявляется в степени изменчивости мыслительной деятельности, соответствующей меняющимся условиям исследуемой ситуации, решаемой проблемы. Противоположное качество - инертность ума - проявляется в склонности к шаблону, к привычным  ходам мысли, в трудности переключения от одной системы действий к другой.

Для развития гибкости (пластичности) мышления учащимся можно предложить следующее задание (на примере данной задачи можно разработать целую серию однотипных задач). Условное название задания «Одинаковые части» (для школьников 5-х – 11-х классов). Учащимся предлагается задание, состоящее из двух частей. В первой части обучающимся задается фигура, которую надо разделить любым способом вначале на 3 части, затем на 4 части, одинаковые по форме и площади, таким образом, чтобы не осталось лишних частей фигуры. Данная фигура (см. рис.1 а) состоит из 12 квадратов (клеточек) и в первом случае при делении распадается на три фигуры ( см. рис. 1 б), каждая из которых состоит из четырех клеточек, а во втором случае, при делении получается четыре фигуры (см. рис. 1 в), состоящие из трех клеточек. В процессе решения задач первой части у учащихся вырабатывается определенный способ решения,  они как бы настраиваются на решение задач одним  способом: фигуру делят ровно по клеточкам.

Во второй части задания учащимся предлагается задача, которая не может быть решена старым способом, хотя по своему внешнему виду задача похожа на предыдущую (тоже фигура, состоящая из одинаковых клеточек, которую нужно делить). Во второй части школьникам задается фигура (квадрат), состоящая из 16 одинаковых клеточек, которую надо разделить любым способом на 5 частей, одинаковых по форме и площади. В инструкции также подчеркивается, что фигуру нужно разделить любым способом без остатка и чтобы не было наложения частей друг на друга.

         

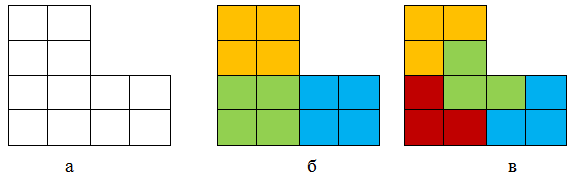
Рис. 1 – Фигура, предъявляемая в первой части задания (а), разделенная на три части (б), на четыре части (в).

Гибкость мышления выражаться в изменении или замене способа решения при обнаружении его несоответствия данным условиям. Другими словами, учащийся становится перед необходимостью отказаться от уже закрепленного способа действий, переделать его и заменить новым. Показателем гибкости мышления выступает, во-первых, способность человека увидеть новый способ в привычной ситуации, а во-вторых, скорость переделки прежнего способа и построения нового. Решение задачи во второй части предполагает другой способ: фигура делится не по клеткам, а «разрезается» на пять частей прямо по клеточкам (получается пять одинаковых прямоугольников).

Решение задач подобного типа и анализ действий школьников во время и после решения показали, что внимание учащихся сфокусировано главным образом на исполнительных действиях, осуществляемых по уже выработанному способу решения, а не на самом способе решения, что говорит о стереотипе действий. При решении задачи второй части учащиеся в основном заняты проблемой деления 16 клеток на 5 частей. Данный способ решения был «перенесен» из первой части задания, когда школьники легко разделили 12 клеток сначала на 3 части (по 4 клетки), а затем на 4 части (по 3 клетки). Для того, чтобы перестроить такие стереотипные действия, необходимо, чтобы школьники систематически анализировали и осмысливали собственную деятельность при решении различного рода как учебных, так и не учебных задач.

К заданию «Одинаковые части» была разработана серия вспомогательных задач, которые последовательно предъявляются учащимся в том случае, если они не могут решить основную задачу. Подсказка 1:  «Ребята, надо делить не клеточки, а фигуру целиком». Подсказка 2: (рисуется пустой квадрат без клеточек) «Разделите данный квадрат на три части, равные по площади и форме». Подсказка 3: «Разделите квадрат на 5 частей».  Разделите вашу фигуру   на 5 частей.

В основе выполнения творческих заданий лежит исследовательский поиск, активизирующий познавательную деятельность учащихся. Решение нестандартной задачи, способ решения которой, как правило, не удается сразу найти, требует длительного и внимательного исследования ее  условий и опробование разных способов поиска. Кроме того, допускаются коллективные обсуждения, столкновения и соотнесения разных точек зрения, разных подходов к решению. Выполняя творческие задания, школьники приобщаются к самостоятельному поиску ответов на возникающие учебно-познавательные проблемы, у них формируются  не только познавательные способности и интересы, но и такие ценные качества личности, как, настойчивость, трудолюбие, самокритичность, активность, объективность.

Список литературы / References

1. Богоявленская Д. Б. Психология творческих способностей / Д. Б. Богоявленская.  – М.: Издательский центр «Академия», 2002. – 320 с.
2. Новиков П. В. Мышление школьника: учебное пособие / П. В. Новиков; Мордов. гос. пед. ин-т. – Саранск, – 152 с.
3. Новиков П.В. Развитие анализа у учащихся в процессе учебной деятельности [Электронный ресурс] / Современные научные исследования. Выпуск 3 / Под ред. П. М. Горева и В. В. Утёмова. - Концепт. - 2015. - ART 85128. - URL: http://e-koncept.ru/2015/85128.htm - ISSN 2304-120X.

 Список литературы на английском языке / References in English

1. Bogoyavlenskaya D.B. Psihologiya tvorcheskih sposobnostej [Psychology of creativity] / D.B. Bogoyavlenskaya. - M.: Izdatelskij centr «Akademiya», 2002. - 320 p. [in Russian]
2. Novikov P.V. Myshlenie shkolnika: uchebnoe posobie [Schoolboy Thinking: Textbook] / P.V. Novikov; Mordov. gos. ped. in-t. - Saransk, 2000. - 152 p. [in Russian]
3. Novikov P.V. Razvitie analiza u uchashchihsya v processe uchebnoj deyatelnosti [Development of the analysis of the students in the process of training activity] [electronic resource] / V. Novikov. - Sovremennye nauchnye issledovaniya [Modern science research]. Vyipusk 3 / Pod red. P.M. Goreva i V.V. Utyomova. - Kontsept. - 2015. - T. 13. - S. 636-640. - ART 85128. / - URL: http://e-koncept.ru/2015/85128.htm - ISSN 2304-120X. [in Russian]